Do, 24.12.2020 Die Frančula Projektionen
Aktualisiert: Sa, 6.11.2021
Anfang dieses Jahres habe ich die Györffy E Projektion auf meine Website aufgenommen. In der Vorbereitung dessen las ich Györffys Abhandlung[1] und stolperte dabei über die Erwähnung des »umbezifferten Aitoff und American Polyconic«. Nun habe ich bereits oft über das Umbeziffern geschrieben, aber noch nie davon gehört, dass dieses Verfahren[2] auf den American Polyconic angewandt wurde. Also stellte ich Nachforschungen an und fand heraus, dass Nedjeljko Frančula bereits 1971 eine Reihe von Projektionen vorgestellt hatte[3], die er mittels Umbeziffern aus verschiedenen Eltern-Projektionen gewonnen worden sind.
Und hier sind sie.
Vierzehn Projektionen, mit Minimierung von Verzerrungen nach dem Kriterium von Airy und Airy-Kavrayskiy.
Ein paar Worte vorweg
Bevor wir uns die Projektionen ansehen, möchte ich ein paar Worte loswerden…
-
Airy-Kriterium? Airy-Kavrayskiy-Kriterium? Was ist das?
Nun, das erkläre ich jetzt nicht. Ich begnüge mich stattdessen mit der Aussage: Es handelt sich um Verfahren, um das Ausmaß der Verzerrungen in einer Kartenprojektion auszudrücken. Theoretisch sollte eine Karte mit einem niedrigen Wert von EA (Airy) oder EAK (Airy-Kavrayskiy) sowohl geringen Winkel-, als auch geringe Flächenverzerrungen haben. Es gibt andere Verfahren, und es gibt Auseinandersetzungen darüber, welches Verfahren am geeignetsten ist.
Frančula hat sich für Airy und Airy-Kavrayskiy entschieden und hat Projektionen vorgelegt, die nach diesen Verfahren minimale Verzerrungswerte zeigen. Es ist durchaus möglich, dass sie nach anderen Verfahren schlechter dastehen. -
Abgesehen von der üblichen Darstellung der tissotschen Indikatrix kann ich leider nur bei zwei Projektionen eine Visualisierung der Verzerrungen zeigen. Das ist ein bisschen ärgerlich, da es bei Frančulas Entwürfen gerade um niedrige Verzerrungen geht.Seit November 2021 enthält dieser Blogpost Visualisierung der Verzerrungen aller Frančula-Projektionen. In Frančulas Originaltext befinden sich ebenfalls Darstellungen der Winkel- und Flächenverzerrungen. Und da dieser Text zum freien Download zur Verfügung steht, kannst Du bei Bedarf dort nachsehen.
In den unten folgenden Tabellen findest Du die Nummer der Anlagen in Frančulas Abhandlung, wo Du die Darstellungen findest. Die Anlagen beginnen auf Seite 72. Wenn zwei Nummern angegeben sind, stellt die erste Grafik die Flächen- und die zweite die Winkelverzerrungen dar. V und XIV haben als flächentreue Projektionen natürlich nur Winkelverzerrungen. Ich weiß nicht, warum die Darstellung der Winkelverzerrungen auch bei einigen anderen Entwürfen fehlt. - Bei den Namen Frančula I bis Frančula XIV handelt es sich nicht um etablierte Bezeichnungen. Soweit ich weiß, gibt es noch keine etablierten Namen; also habe ich ihnen einfach diese verpasst. Die Ordnungszahlen entsprechen der Reihenfolge, in der die Projektionen in Frančulas Abhandlung aufgelistet werden.
- Die Frančula-Projektionen wurde durch Umbeziffern von fünf Eltern-Projektionen abgeleitet. Vier davon wurden schon von Wagner benutzt, daher bezeichne ich die entsprechenden Entwürfe Frančulas als »Wagner-Varianten«.
- Frančula hat die Projektionen ausdrücklich für die Verwendung von allgemein-geographischen Karten in Atlanten entworfen, wies aber darauf hin, dass sie auch für diverse thematische Karten geeignet sind. Folglich sehen sie mehr oder weniger so aus, wie man es kennt: Weltkarten mit Pol-Linie, äquatorständig und ohne Unterbrechungen. Erwartet keine ungewöhnlichen, überraschenden Projektionen!
-
Und last, but not least:
Ich hätte Euch diese Projektionen nicht zeigen können, wenn ich nicht große Hilfe von Peter Denner erhalten hätte. Aufbauend auf meiner vorläufigen Implementation des anpassbaren Wagner IX hat er eine vollständige Version geschrieben, welche neben allgemeinen Verbesserungen auch die Möglichkeit geschaffen hat, das Umbeziffern auf andere Projektionen anzuwenden.
Herzlichen Dank, Peter!
Die komplette Implementation für d3-geo-projections wird in naher Zukunft separat vorgestellt werden.
Nach dieser Vorrede können wir endlich zu den Projektionen selbst kommen.
Frančula I – Frančula V
Die Projektionen Frančula I bis Frančula V wurden für geringst mögliche Verzerrungswerte nach dem Airy-Kriterium (EA) optimiert; kleinere Werte stehen dabei für geringere Verzerrungen, sind also besser. I bis IV haben gleichabständige Breitenkreise (entlang des Zentralmeridians) und gehören zum Typus der aphylaktischen (vermittelnden) Projektionen; Nr. V ist flächentreu.
Obwohl die pseudozylindrischen Projektionen I und II tatsächlich niedrige Verzerrungswerte aufweisen, sehen sie, weil sie in Nord-Süd-Richtung stark gestreckt werden, meiner Meinung nach nicht gerade ansprechend aus. Die lentikulären Projektionen III und IV gefallen mir deutlich besser und zeigen darüber hinaus auch bessere EA-Werte. Da sie sich auf den ersten Blick einigermaßen ähnlich sehen, hier der Link zum direkten Vergleich.
Frančula V hat die höchsten Verzerrungswerte, kann dafür mit der oft nützlichen Eigenschaft der Flächentreue punkten. Nebenbei bemerkt, sieht mein eigenes Experiment, das ich Wagner BCW-E genannt habe, nicht unähnlich aus (aber ich verspreche, ich wusste nichts über Frančulas Projektionen, als ich den BCW-E entworfen habe).
Frančula VI – Frančula IX
Die Projektionen VI bis IX wurden ebenfalls nach dem Airy-Kriterium entworfen, dabei kamen
Elternprojektionen zum Einsatz, die schon bei Frančula I bis III genutzt worden sind.
Warum das?
Nun, die ersten Varianten weisen eine Schnittparallele
(und damit das Gebiet der geringsten Verzerrungen) um 60° Nord/Süd auf, was nicht
nur für ihre längliche Form verantwortlich ist, sondern auch – trotz niedriger Gesamt-Verzerrungen –
für eine ungünstige Verteilung der Verzerrungen sorgt.
Um dies zu beheben, setzte Frančula die Schnittparallele in den Projektionen VI und VII auf 40° Nord/Süd und modifizierte die Länge der Pol-Linie, um auch in dieser Konfiguration Minimum-Werte von EA zu erreichen. Das Ergebnis sieht in meinen Augen tatsächlich besser aus und ist wahrscheinlich auch geeigneter für den geplanten Einsatzzweck als allgemeinen-geographische Karten.
So weit, so gut. Aber die Variationen vom Francula III, das sind Frančula VIII und IX,
verwirren mich. Die Idee ist die gleiche, nämlich die Verteilung der Verzerrungen zu verbessern. Aber…
Erstmal sehen sie für mich weniger ansprechend aus als die Nr. III. Gut, das ist
eine rein ästhetische Einschätzung, also vergessen wir das.
Zweitens bin ich nicht so sicher, on die Verteilung der Verzerrungen wirklich besser ist.
Sicher, die Größenverzerrungen im Verhältnis zum nominellen(!) Maßstab der Karte sind
ausgeglichener, aber ich finde, dass sich die Verteilung der Winkelverzerrungen ein bisschen verschlechtert.
Aber vor allem frage ich mich, dass der Frančula VIII überhaupt aufgeführt wird,
da doch der IX fast identisch aussieht, allerdings über einen geringeren
EA-Wert verfügt. Ich hätte Nr. VIII unter diesen Umständen einfach
verworfen…
Nun, ich kenne den Grund nicht, und wenn er im Dokument genannt wird, ist es mir
bisher gelungen, stets darüber hinwegzulesen. Wie auch immer:
Frančula VIII und IX im direkten Vergleich
– man muss schon genau hinschauen, um die Unterschiede zu sehen.
Um die Änderungen zur ersten Ausführung zu inspizieren:
Vergleiche Frančula III und IX.
Bevor wir zur zum nächsten Abschnitt übergehen, folgt hier eine Tabelle
aller Frančula-Projektionen, die wir bisher hatten, nebst einiger bekannter Projektionen,
sortiert nach dem EA-Wert, vom besten zum schlechtesten.
Alle Werte habe ich aus Frančulas Abhandlung übernommen.
| Projektion | EA |
|---|---|
| Frančula IV | 0.2745 |
| Frančula III | 0.2797 |
| Frančula I | 0.3087 |
| Frančula II | 0.3115 |
| Frančula V ∗ | 0.3172 |
| Frančula IX | 0.3218 |
| Winkel Tripel (Orig.) | 0.3280 |
| Frančula VIII | 0.3303 |
| Winkel Tripel Bartholomew | 0.3674 |
| Frančula VI | 0.3825 |
| Frančula VII | 0.3830 |
| Eckert V | 0.4012 |
| Eckert VI | 0.4025 |
| Eckert IV ∗ | 0.4068 |
| Kavraiskiy VII | 0.4126 |
| Mollweide ∗ | 0.4419 |
| Hammer ∗ | 0.4654 |
| Aitoff | 0.5041 |
| Sinusoidal ∗ | 0.5581 |
|
∗ flächentreu Kleinere Werte von EA sind besser |
|
Frančula X – Frančula XIV
Die letzten fünf Projektion sind von den gleichen Eltern abgeleitet wie zuvor, aber wurden für niedrige Verzerrungswerte nach dem Airy-Kavrayskiy-Kriterium optimiert. Meiner Meinung nach sehen die pseudozylindrischen Projektionen X und XI viel besser aus als ihre Airy-Gegenstücke. Bei den lentikulären fällt es mir schwerer, mich zu entscheiden: Sie unterscheiden sich zwar deutlich, dennoch sehen sowohl die Airy-, als auch die Airy-Kavrayskiy-Varianten angenehm aus.
Obwohl sie von unterschiedlichen Eltern-Projektionen abgeleitet sind, sehen
Frančula XII and XIII recht ähnlich aus.
Vergleich sie direkt, um die Unterschiede zu sehen.
Und wieder hat die flächentreue Projektion (XIV) die höchsten Verzerrungswerte, aber sie sind
immer noch sehr gut. Abgesehen von der ausgeprägteren Streckung in Nord-Süd-Richtung sieht
sie einer Variante, die Wagner selbst 1941[4] vorgestellt hat,
sehr ähnlich. Ich habe sie Wagner VII.d benannt:
Vergleiche Wagner VII.d und Frančula XIV.
Und hier nun die Tabelle mit den EAK-Werten von Frančula X bis Frančula XIV, im Vergleich zu den gleichen bekannten Projektionen wie oben, plus Robinson und Eckert III: [5]
| Projektion | EAK |
|---|---|
| Frančula XIII | 0.2359 |
| Frančula XII | 0.2388 |
| Frančula XI | 0.2490 |
| Frančula X | 0.2498 |
| Winkel Tripel (Orig.) | 0.2597 |
| Winkel Tripel Bartholomew | 0.2603 |
| Kavraiskiy VII | 0.2614 |
| Robinson | 0.2778 |
| Eckert III | 0.2853 |
| Eckert V | 0.2972 |
| Frančula XIV ∗ | 0.3177 |
| Eckert IV ∗ | 0.3326 |
| Eckert VI | 0.3496 |
| Aitoff | 0.3690 |
| Mollweide ∗ | 0.3774 |
| Hammer ∗ | 0.4096 |
| Sinusoidal ∗ | 0.4701 |
|
∗ flächentreu Kleinere Werte von EAK sind besser |
|
Ein paar Anmerkungen zu Verzerrungen
Während ich an diesem Blogpost schrieb, wurde mir folgendes mitgeteilt:
»Im Gegensatz zum Airy-Kavrayskiy-Kriterium bewertet das Airy-Kriterium
horizontale Kompression / vertikale Streckung anders als
horizontale Streckung / vertikale Kompression um den gleichen Faktor.«
Daher sind Frančula I bis V, VIII und IX alle vertikal gestreckt (oder horizontal komprimiert),
besonders die ersten beiden. (VI und VII sind Ausnahmen, da Frančula hier absichtlich vom
Prinzip, die kleinstmöglichen Wert von EA zu erreichen, abgewichen ist.)
Dies wollte ich nur deshalb erwähnen, weil es einiges erklärt.
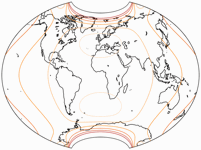
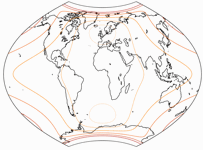
Wie ich zu Beginn gesagt habe, kann ich derzeit nur von zwei Projektionen, nämlich Frančula V und XIV, eine Visualisierung der Verzerrungen zeigen. Da beide flächentreu sind, gibt es nur Winkelverzerrungen. Zum Vergleich füge ich den originalen Wagner VII hinzu.
Hellere Farbtöne zeigen geringere, dunklere Farbtöne höhere Verzerrungswerte an.
Die roten Linien markieren eine maximale Winkelverzerrung von 40° und 80°.
Es ist immer das gleiche, wenn man Parameter einer Projektion verändert: Manche Teile der
Erde gewinnen, andere verlieren; und es ist schwierig zu sagen, welche Variante
insgesamt die bessere ist (und das ist der Grund, warum man sich so Sachen wie die
Airy und Airy-Kavrayskiy-Kriterien ausgedacht hat).
Also belasse ich es dabei, dass in Bezug auf die Verteilung von Verzerrungen in meinen Augen
alle drei geeignet für die Atlaskartographie sind.
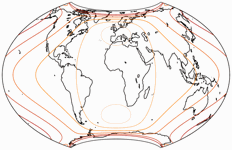
UPDATE 6.11.2021: Visualisierung der Verzerrungen
Oben habe ich gesagt, ich könne nur von zwei Frančula-Projektionen eine Visualisierung der Verzerrungen zeigen. Dank Peter Denner kann ich aber nun alle 14 in entsprechender Darstellung präsentieren! 🙂
Isolinien der Winkelverzerrungen
Die Linien werden gezeigt für eine max. Winkelverzerrung von:
10°,
20°,
30°,
40°,
50°,
und 60°.
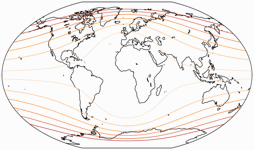
Isolinien der Flächenvergrößerungen
Die flächentreuen Projektionen Frančula V und XIV werden hier natürlich weggelassen. Bitte beachte, dass die Linien im Verhältnis zum Wert in der Mitte der Karte berechnet wurden! Meistens werden sie im Verhältnis zum nominellen Maßstab der Karte gezeigt. Sie werden gezeigt für eine Flächenvergrößerung von:
1,5;
2,0;
2,5;
3,0;
und 3,5.
Fazit
Frančula hat 14 Projektionen mit niedrigen Verzerrungswerten vorgelegt. Erfüllen sie den Anspruch,
»vorteilhafte Abbildungen für die Atlaskartographie« zu sein?
Hier ist meine persönliche Meinung dazu:
Frančula I und II: Nun, die können nützlich sein, wenn Du unbedingt eine pseudozylindrische Projektion auf kleinem Raum unterbringen musst. Ich würde sie nicht für eine allgemein-geographische Karte empfehlen, aber für die eine oder andere thematische Karte könnte man sie vielleicht benutzen. Obwohl ich zugeben muss, dass ich da keinen Vorteil gegenüber altbekannten Projektionen sehe (etwa dem Wagner III mit entsprechender Schnittparallele).
Frančula III und IV, VIII und IX: Vertikal immer noch ziemlich gestreckt, aber ästhetisch gesehen gefallen sie mir gut. Ich denke, sie eignen sich durchaus für die Atlaskartographie, wenn man horizontal etwas Platz sparen will. In den Atlanten, die ich kenne, gibt es allerdings gerade in dieser Richtung eher keine Platzprobleme. Daher würde ich sie wohl eher für (meistens kleiner dargestellte) thematische Karten verwenden als für die Hauptkarten (denen eher viel Platz zugestanden wird). Darüber hinaus sollten sie sich auch für allgemein-geographischen Wandkarten eignen, bei denen ästhetische Erwägungen eine stärkere Rolle spielen.
Frančula VI und VII, X bis XIII: In dieser Reihe sind in meinen Augen alle geeignet für allgemein-geographische Karten in Atlanten (und gleichermaßen als Wandkarte), so dass man sich eine gemäß seiner persönlichen Vorlieben und Anforderungen aussuchen kann. Ich selbst bevorzuge die Reihe der nach Airy-Kavrayskiy optimierten Projektionen und hier die lentikulären.
Die flächentreuen Frančula V und XIV: Beide sind für den genannten Zweck geeignet. Beide Projektionen haben ihre Vor- und Nachteile, unterm Strich würde ich Nr. XIV vorziehen.
Fazit des Fazits: Außer Frančula I und II
sind meiner Meinung nach alle Projektionen geeignet für die Atlas-Kartographie.
Manche mehr als andere – in Bezug auf das übliche Layout von Atlanten, die ich kenne.
Aber selbst diese »anderen« können sich in bestimmten Situationen als wertvoll
erweisen.
Auf jeden Fall sind sie interessante Alternativen zu den »üblichen Verdächtigen«
wie Robinson, Winkel Tripel usw.
Györffys Anmerkung zur Form
Eingangs habe ich gesagt, dass ich auf die Frančula-Projektionen aufmerksam wurde, als die Györffys Abhandlung gelesen habe. Folgendes hat er genau gesagt:
(…) some projections were created representing the poles as concave curves (bent towards the equator) by suitable renumbering of Aitoff and ordinary polyconic, with even lower EK values (…) They are ignored in the praxis of cartography because of their appearance.
(…)
The shape of the mapped Earth in the renumbered Aitoff and ordinary polyconic (…) suggest that a minimized distortion projection, representing the pole as a line, generates an outline with concave pole lines (…) The unfamiliar shape of the mapped Earth provokes the neglect of these projections.
Durch angemessenes Umbeziffern wurden aus dem Aitoff und der polykonischen Projektion einige Entwürfe mit konkaver Pollinie geschaffen, die noch niedrigere EK-Werte aufweisen. Aufgrund ihres Erscheinungsbildes werden sie in der kartographischen Praxis ignoriert.
(…) Die Form der abgebildeten Erde im umbezifferten Aitoff und polykonischen Entwurf legt nahe, dass eine Projektion mit minimierten Verzerrungen, welche die Pole als Linie darstellt, eine Kontur mit konkaver Pollinie erzeugt. (…) Die ungewohnte Form der abgebildeten Erde verursacht, dass diese Projektionen nicht verwendet werden.
Augenscheinlich ist es richtig, dass die Frančula-Projektionen bisher »in der kartographischen Praxis ignoriert« worden sind – jedenfalls kann ich mich nicht erinnern, sie jemals irgendwo gesehen zu haben. Györffys Begründung für diesen Umstand kann ich aber nicht zustimmen. Das Erscheinungsbild ist höchstens einer der möglichen Gründe; aber es gibt meiner Meinung nach keinen Hinweis, dass dies auch der tatsächliche Grund ist.
Wie auch immer, wenn Dir der Frančula XIII im Prinzip gefällt, Dich aber die konkaven Pollinien stören … schneide die polaren Regionen einfach ab:
Und wenn Du nun meinst, so eine Beschneidung sei ein schlechtes Vorgehen, stimme ich sogar zu (sogar unter Nicht-Berücksichtigung der Tatsache, dass ich die konkaven Pollinien ja mag). Allerdings habe ich schon schlimmere Beschneidungen gesehen, auch in Atlanten. Und obwohl die diese Vorgehensweise nicht mag, muss ich zugeben, dass man nichts abschneidet, was bei einer allgemein-geographischen Karte wichtig wäre. Hier sind die Teile, die abgeschnitten wurden – ich denke, damit kann man leben:
Und ein Experiment
Aus reiner Neugierde habe ich durch das Anwenden von Umbeziffern eine Projektion geschaffen, die eine gewisse Ähnlichkeit mit dem Frančula XIII hat – Länge und Krümmung von Pollinien und den begrenzenden Meridianen entsprechen weitgehend vom Vorbild –, allerdings den flächentreuen Azimutalentwurf mit »vorgeschriebener Flächenverzerrung« (wie Wagner es genannt) hat als Eltern-Projektion verwendet, wodurch sie zu einer Variante von Wagner VII/VIII wird. Ich habe mich für eine Konfiguration entschieden, die im Vergleich zum Frančula XIII auf eine geringere Flächenverzerrung hinausläuft.
Mir gefiel das Ergebnis zwar, aber zunächst war ich nicht sicher, ob ich es auf die Website aufnehmen soll… aber dann fiel mir etwas auf: Bei der Verwendung von Richard Capeks Verzerrungswert Q[6] (ein weiteres der o.g. Verfahren, das Ausmaß der Gesamtverzerrungen in einer Kartenprojektion zu ermitteln), erreichte mein Experiment einen Wert von 88,1 – was hervorragend ist, oder genauer: Besser als alle der 100 (nicht unterbrochenen) Projektionen, die in Capeks Abhandlung gelistet sind!
Zugegeben, das Q von meiner Projektion wurde
nicht per Berechnung aus der Formel ermittelt, sondern über eine
Art von Kartometrie (über die ich irgendwann in nächster Zeit
einen langen und ermüdenden Blogpost schreiben werde); außerdem
hat Q gewisse Defizite (darauf werde ich im erwähnten Blogpost
eingehen) und natürlich gibt es Projektionen, die von Capek nicht untersucht wurden
und die einen noch besseren Q-Wert aufweisen mögen…
… Aber es war trotzdem eine schöne Überraschung! 😊
Also hier ist er, mein… Halt, wie soll ich die neue Projektion denn nun nennen?
Sie ist vom Frančula XIII inspiriert, also sollte es einen Bezug zu diesem Namen geben.
Sie ist mit Sicherheit keine Approximation, denn die Verteilung der Meridiane und
Breitenkreise unterscheidet sich erheblich.
Ach… ich nenne sie einfach den F13 Nachahmer oder englisch F13 Copycat.
Ich zeige diesmal eine andere Darstellung der Verzerrungen, nämlich die Linien gleicher Flächenmaßstäbe und Winkelverzerrungen, wodurch es leichter wird, sie mit den entsprechenden Abbildungen der Projektion XIII in Frančulas Abhandlung (siehe Seite 86, Anlage 25 und 26) zu vergleichen.
Du wirst bemerken, dass die Linie, welche eine Flächenvergrößerung von 3,0 anzeigt,
entlang der Breite von 80° Nord/Süd verläuft, ganz ähnlich wie beim Frančula XIII.
Warum sage ich also, dass der Nachahmer eine »geringere Flächenverzerrung« aufweist?
Beachte, dass Frančulas Entwurf in der Mitte der Karte eine Flächenverzerrung von
0,77 zeigt (hier werden Flächen also verkleinert dargestellt), der Nachahmer
aber 1,0 (= flächentreu entlang des Äquators), folglich hat letzterer
insgesamt tatsächlich eine geringere Flächenvergrößerung.
Oder, genauer gesagt, eine geringere Varianz an Flächenverzerrungen.
Bei den Winkelverzerrungen hingegen zeigt Frančulas Original eindeutig die besseren Verteilungen, aber das war zu erwarten.
Die Böhm-Notation des F13 Copycat lautet vii@60-77-60-45-170.
Um den Entwurf in Geocart
zu erzeugen, verwende den generalized Wagner mit folgenden Parametern:
a = 2.148298
b = 1.573349
m = 0.953264
m2 = 0.725519
n = 0.427778
oder nutze die d3-geo-projection-Skripte mit:
d3.geoWagner()
.poleline(60)
.parallels(77)
.inflation(45)
.ratio(170)
Fußnoten
-
↑
János Györffy: Minimum distortion pointed-polar projections for world maps by applying graticule transformation
(engl.)
doi.org/10.1080/23729333.2018.1455263 -
↑
Wagners Umbeziffern und die Böhm-Notation:
kartenprojektionen.de/wagner-umbeziffern.php - ↑ Nedjeljko Frančula: Die vorteilhaftesten Abbildungen in der Atlaskartographie
-
↑
Wagner, Karlheinz:
Neue ökumenische Netzentwürfe für die kartographische Praxis.
In: E. Lehmann, ed., Jahrbuch der Kartographie 1941.
Leipzig: Bibliographisches Institut. 176–202. - ↑ Die EAK-Werte von Robinson und Eckert III entstammen nicht Frančulas Abhandlung, sondern der von Györffy. Beachte, dass Györffy sein EK anders berechnet, die Werte lassen sich aber ineinander überführen, indem man Györffys EK durch die Quadratwurzel von 2 teilt – oder umgekehrt Frančulas EAK mit √2 multipliziert.
-
↑
Capek, Richard 2001:
Which is the Best Projection for the World Map?
icaci.org/files/documents/ICC_proceedings/ICC2001/icc2001/file/f24014.pdf































 Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Kommentare
Sei der erste, der einen Kommentar hinterlässt!