Die Sinucyli-Projektion

Fr, 27.10.2017 Die Sinucyli-Projektion

3 mal aktualisiert, zuletzt Do, 4.1.2018

Nach dem letzten Update hatte ich genau 199 Projektionsgrafiken in der Liste meiner Website. Es handelte sich natürlich nicht um 199 verschiedene Projektionen, denn etliche Entwürfe werden ja in unterschiedlichen Konfigurationen gezeigt. Trotzdem wollte ich für die Nr. 200 irgendetwas Besonderes haben. Und ich denke, das ist mir gelungen!

Denn Sinucyli-Projektion, die ich als Nr. 200 aufgenommen habe, ist ganz neu – so neu, dass sie bisher noch nicht einmal offiziell vorgestellt wurde zum Zeitpunkt, als dieser Blogpost erschien, noch nicht einmal offiziell vorgestellt worden war. Trotzdem hat mir ihr Urheber, Daniel »daan« Strebe, freundlicherweise erlaubt, sie schon jetzt vorher auf meiner Website zu zeigen. Vielen Dank nach Seattle! :-)

Die Sinucyli-Projektion ist eine flächentreue pseudozylindrische Projektion (oder auch unecht-zylindrisch, wie deutsche Kartographen meist sagen). Das ist nichts Besonderes, davon gibt es Dutzende.
Sie ist eine Mischung aus der flächentreuen Zylinder- und der sinusoidalen Projektion. Auch das ist nichts Besonderes, das Mischen von Projektionen ist eine altbekannte Verfahrensweise: Der beliebte Winkel Tripel z.B. ist das arithmetische Mittel aus der rechteckigen Plattkarte und dem Aitoff-Entwurf. Die Software Flex Projector erlaubt es, zwei fast beliebige Projektionen miteinander zu verschmelzen – darunter auch die beiden Eltern-Projektionen der Sinucyli.

Was ist also so interessant an diesem neuen Entwurf? – Nun, er hat zwei Besonderheiten:

Durch vier leicht verständliche Konfigurations-Parameter kann die Mischung der beiden Elternprojektionen den eigenen Wünschen angepasst werden. Dies resultiert in höchst unterschiedlichen Ergebnissen (einige Beispiele folgen unten).
Update: Die wichtigste Besonderheit aber war mir selbst noch nicht bekannt, als ich diesen Blogpost veröffentlich habe. Die Sinucyli-Projektion ist nämlich eigentlich nur ein Beispiel. Ein Beispiel für eine neue, von Mr. Strebe entwickelte Technik, zwei beliebige flächentreue Projektionen mit beliebiger Gewichtung miteinander zu mischen, wobei das Resultat stats flächentreu bleibt – das unterscheidet die neue Technik von bekannten Methoden (z.B. dem oben erwähnten arithmetischen Mittel).

Dies ist einerseits interessant, weil die Flächentreue für viele Anwendungsgebiete eine sehr nützliche Eigenschaft darstellt und das Verfahren den Anwender in die Lage versetzt, eine eigene Projektion, die den aktuellen Bedürfnissen entspricht, zu kreieren.
Vor allem aber ist diese Technik »particularly suited to maps that dynamically adapt optimally to changing scale and region of interest, such as required for online maps« (besonders geeignet für Karten, die sich optimal dynamisch an wechselnde Maßstäbe und Kartenmittelpunkte anpassen, wie es für Online-Karten notwendig ist). ^[1]

Bleiben wir aber bei dem Beispiel der Mischung von der flächentreuen Zylinder- und der sinusoidalen Projektion und sehen uns die vier o.g. Konfigurations-Parameter mal genauer an.

Die Konfigurationsparameter der Sinucyli-Projektion mit dem entsprechenden Resultat
(Screenshot aus der Projektionssoftware Geocart)

Weight of sinusoidal (Gewichtung der Sinusoidal-Projektion) legt das Mischverhältnis der beiden Eltern-Projektionen fest. Ein Wert von 1 entspricht genau der Sinusoidalen, es wird also gar nicht gemischt. Das ist nicht so ganz Sinn der Sache, [Update:] falls man eine einzelne Projektion erzeugen will, ist aber hilfreich bei dynamischen Karten oder Animationen.
Zur Null hin verstärkt sich der Anteil der flächentreuen Zylinderprojektion. Ein Wert von genau 0 ist nicht möglich, aber wenn man unbedingt will, kann man durch Eingabe von 0.0000001 o.ä. eine Projektion erzeugen, die praktisch mit der zylindrischen identisch ist führt abermals dazu, dass nicht gemischt wird, es wird also reine »reine« zylindrische Projektion erzeugt. (Hinweis: Die Eingabe von Null wurde in der aktuellen Beta-Version ermöglicht.)
Der im Screenshot gezeigte Wert von 0.5 liegt also genau auf halbem Wege zwischen den beiden Projektionen.

Weighted axis (gewichtete Achse) legt fest, ob sich der obige Wert auf die horizontale oder die vertikale Achse der Sinusoidal-Projektion bezieht. Das ist im ersten Moment vielleicht nicht so einfach zu verstehen, wie ich oben versprochen habe – es läuft aber darauf hinaus, dass der Wert Vertical punktförmige Pole erzeugt, während man bei Horizontal eine Projektion mit Pol-Linie erhält.

φ₁ ist die Schnittparallele des zylindrischen Anteils. Wie üblich gilt: Je höher dieser Wert (der logischerweise zwischen 0 und 90 liegen darf) ausfällt, desto schmaler wird das Ergebnis.

Vertical stretch of sinusoidal (vertikale Streckung der Sinusoidal-Projektion) hingegen beeinflusst das Seitenverhältnis des sinusoidalen Anteils. Werte über 1 ziehen das Ergebnis in die Länge, Werte zwischen 0 und 1 in die Breite.

Es mag zunächst so erscheinen, als ob die Parameter Nr. 3 und 4 mehr oder weniger die gleichen Auswirkungen haben. Tatsächlich sind sie aber unterschiedlich – das möchte ich anhand des folgenden Beispiels zeigen.
– Beide Karten wurden mit einer Gewichtung von 0,7 erzeugt, mit der Auswahl horizontal für die gewichtete Achse.
– Bei der linken Karte wurde mit φ₁ = 0 ein Wert gewählt, der in die Breite zieht, was durch die vertikale Streckung von 2 kompensiert wurde.
– Bei der rechten Karte bin ich genau umgekehrt vorgegangen: φ₁ = 80°N zieht in die Länge, der Streckungs-Wert von 0,93 wirkt dem entgegen.
Die beiden Ergebnisse sind exakt gleich hoch, darüber hinaus zeigen sie aber keine großen Ähnlichkeiten:

Ich denke, es ist also leicht zu begreifen, was die einzelnen Werte besagen – spätestens, wenn man ein bisschen mit ihnen experimentiert hat.
Kommen wir nun zu den drei Varianten, die ich auf die Website aufgenommen habe.

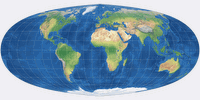
Bei der ersten handelt es sich um die Konfiguration, welche schon oben im Screenshot zu sehen war (und von Geocart per Default erzeigt wird); mit den Parametern 0.5 / Vertical / 29°30´N / 1 stellt sie einen guten Mittelwert als Startpunkt für eigene Experimente dar.
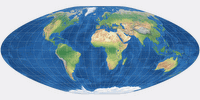
Die zweite (0.25 / Vertical / 29°30´N / 1.1) zeigt eine Projektion, welche sich einer rechteckigen Form annähert, aber einen punktförmigen Pol aufweist.
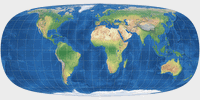
Die dritte hingegen nähert sich mit den Werten 0.8 / Horizontal / 30°N / 1 eher der Sinusoidalen an, zeigt aber eine kurze Pollinie.

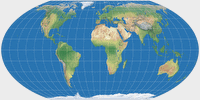
Es ist nicht sehr erstaunlich, dass man mit der Sinucyli-Projektion andere flächentreue Pseudozylinder approximieren kann bzw. dass sie sogar Spezialfälle der Sinucyli darstellen. In jeweils eine dieser beiden Kategorien fallen z.B. Kavraisky V, Quartic Authalic, Eckert IV, Thomas-MyBryde flat-pole quartic oder Wagner IV.
Und falls Du die naheliegende Frage stellst, warum Du das denn tun solltest, da Du stattdessen doch auch direkt zum jeweiligen Original greifen kannst: Nun, vielleicht hast Du Dir schon mal eine dem Eckert IV ähnliche Projektion, aber mit kürzerer Pollinie gewünscht – oder vielleicht den Wagner IV mit abgerundeten Ecken. Derartige »Sonderwünsche« können vom Sinucyli-Entwurf erfüllt werden. Hier ein Beispiel:

Wie oben erwähnt, ist eine derart konfigurierbare Projektion hilfreich für dynamische Karten und Animationen. Also habe ich mal schnell eine kleine Animation zusammengestellt: Die Parameter #3 und #4 bleiben in allen Bildern gleich (nämlich bei 29°30´N für die Schnittparallele und einer vertikalen Streckung von 1), aber die Parameter #1 und #2 werden variiert:
Sie beginnt mit einer Gewichtung von 1 der vertikalen Achse, verringert die Gewichtung dann schrittweise bis hin zu 0, wo sie auf die horizontale Achse wechselt und die Gewichtung wieder bis hin zur 1 erhöht.
Zeige die Animation!
(Ich entschuldige mich für ein paar Ungenauigkeiten, die z.B. dafür sorgen, dass der Äquator blinkt. Beim nächsten Mal mache ich es besser…)

Ich möchte es noch einmal betonen: Du wirst mit der Sinucyli-Projektion keine überraschenden, ungewohnten Ergebnisse erzeugen!
Das dürfte bei der gut ausgebauten Familie der flächentreuen pseudozylindrischen Entwürfe auch kaum machbar sein. Aber die Möglichkeit, auf einfache Weise eigene Konfiguration zu erstellen, halte ich für nützlich genug, um die Sinucyli als wertvolle Ergänzung im Bereich der Kartenprojektionen anzusehen.

Und wie kannst Du die Sinucyli-Projektion nutzen?
Jetzt kommt leider die schlechte Nachricht: Im Moment noch gar nicht.
Sie wird in der nächsten Version der Kartenprojektions-Software Geocart enthalten sein – wann die erscheint, ist allerdings noch offen. Und sobald daan Strebe die Formel veröffentlicht, kann sie natürlich in jede andere Software eingebaut werden. Ich werde es an dieser Stelle melden, sobald ein entsprechende Veröffentlichung verfügbar ist.
Update! Im Februar 2018 wurde die Version 3.2 von Geocart veröffentlicht, diese Version enthält auch die Sinucyli-Projektion (neben vielen anderen zusätzlichen Projektionen). Die Technik wurde offiziell vorgestellt und kann somit in andere Programme eingebaut werden, siehe unten.