Neues auf kartenprojektionen.de

Mo, 1.1.2018 Neues auf kartenprojektionen.de

Aktualisiert: Mo, 10.1.2022

Wie kann man ein neues Jahr besser beginnen, als mit einem Update der Website?
;-)

Geänderte Grafiken für die Darstellung der tissot’schen Indikatrix

Beginnend mit den Projektionen, die ich heute hinzugefügt habe (s.u.), werde ich geänderte Grafiken für die tissot’sche Indikatrix verwenden. Ich habe die Farben geändert, um bessere Kontraste zu erreichen; das Gradnetz (welches bei der Beurteilung von Verzerrungen ebenfalls hilfreich ist) wird stärker hervorgehoben; die Artefakte an den Küstenlinien habe ich entfernt:

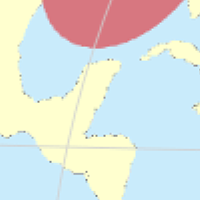
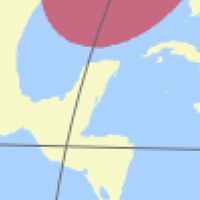
Ich werde diese Grafiken aber nur bei Projektionen verwenden, die ich neu hinzufüge; die bisherigen Tissot-Grafiken werden also nicht ersetzt. Zumindest nicht in absehbarer Zeit – das wäre viel Arbeit, und da die bisherigen Grafiken meiner Meinung nach nicht wirklich schlecht sind, lohnt sich der Aufwand nicht.
Vielleicht werde mir eines Tages die Zeit nehmen und auch die alten Darstellungen ersetzen… aber vielleicht auch nicht.
Update 10.1.2022: Und vier Jahre später habe ich mir nun doch die Zeit genommen – die alte Tissot-Darstellung wurde nun endlich für alle Projektionen durch die neuen ersetzt!

Neue Projektionen: Erst die Arbeit, dann das Vergnügen

Die erste Reihe an neuen Projektionen habe ich hinzugefügt, obwohl ich, ehrlich gesagt, keine große Lust dazu hatte. Es handelt sich ausschließlich um flächentreue Zylinderprojektionen.
Bezüglich dieser Art von Projektionen bin ich der Meinung, dass man sie nur äußerst selten verwenden kann/sollte:
– Wenn Du eine flächentreue Karte willst, wähle keine Zylinderprojektion.
– Wenn Du eine Zylinderprojektion willst, wähle keine flächentreue Karte.
Eine flächentreue Karte in die rechteckige Form zu pressen, führt zwangsläufig zu erheblichen Verzerrungen der Formen. Die Vorteile einer rechteckigen Karte sind in meinen Augen nicht groß genug, um diese Verzerrungen hinzunehmen.

Darüber hinaus unterscheiden sich alle flächentreuen Zylinderprojektionen nur in einem Punkt, nämlich der ausgewählten Schnittparallele. Ich finde es ziemlich unnötig, neun individuelle Namen zu vergeben, wenn es sich letztendlich um ein und dieselbe Projektionsmethode handelt, bei der nur ein einzelner Parameter geändert wurde.
Zugegeben: Die meisten dieser Projektionen wurden zu einem Zeitpunkt entworfen, als das Zeichnen einer neuen Karte mit geänderter Schnittparallele noch deutlich aufwendiger war, als einen beliebigen Wert zwischen 0 und 90 einzutippen, einen Button anzuklicken und zu warten, bis die Projektionssoftware die Karte fertig gerendert hat. Also, vielleicht sind die vielen unterschiedlichen Namen berechtigt, auch wenn es aus heutiger Sicht etwas ungeschickt wirken mag.

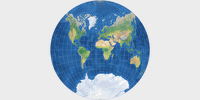
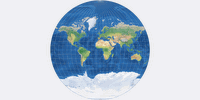
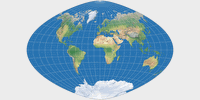
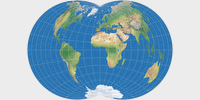
Vor allem aber ist kartenprojektionen.de ja gerade dazu geschaffen worden, ähnliche Projektionen vergleichen und ihre manchmal sehr geringfügigen Unterschiede entdecken zu können. Was rede ich also so lange herum? – Hier sind die neu aufgenommenen flächentreuen Zylinderprojektionen: Balthasart, Smyth, Tobler’s Welt in einem Quadrat und Trystan-Edwards (in der von John P. Snyder korrigierten Variante) ^[1].

Nun zu dem Teil, der mit mehr Spaß gemacht hat als die obige Pflichtübung.
Der van der Grinten I ist auf dieser Website schon enthalten, seitdem sie erstmalig online gegangen ist. Zweieinhalb Jahre später ist es nun auch an der Zeit, die seltener verwendeten van der Grinten II, III und IV nachzureichen.
Die Nummerierung wird allgemein so verwendet – was ein wenig verwirrend sein mag, ist die Tatsache, dass – die Projektionen I und IV 1904 von Alphons J. van der Grinten selbst vorgestellt wurden; – die Entwürfe II und III aber erst später erschienen sind, es handelt sich dabei um Modifikationen des van der Grinten I, welche Alois Bludau 1912 vorgestellt hat ^[2].

Bei der Beschäftigung mit van der Grinten stieß ich auf das arithmetische Mittel aus van der Grinten I und der Aitoff-Projektion, die John J. G. Savard seit 2007 auf quadibloc.com zeigt.
Mir gefiel dieses Ergebnis irgendwie, also habe ich meine eigene Variante davon hergestellt – in dieser Variante ist die Gewichtung der beiden gemischten Projektionen verschoben, sie besteht nun aus 65% Aitoff und 35% van der Grinten.
Aufgrund dieses Mischverhältnisses habe ich dem Entwurf den Namen Aitoff-van-der-Grinten 65 verpasst. Ich glaube nicht, dass er sich für irgendwelche Zwecke eignet außer für rein dekorativen Karten.

… und der van der Grinten IV mit seinen zwei Flügeln oder Segeln oder wie auch immer man das nennen mag (ich selbst nenne derartige Entwürfe immer Zellteilungs-Projektionen; aber nur, wenn keiner zuhört), hat mich zum flächentreuen Dietrich-Kitada ^[3] gebracht:

Als nächstes habe drei sehr ungewöhnliche flächentreue Projektionen aufgenommen: Snyders Tetraeder, sowie die ebenfalls tetraederförmige Projektionen von van Leeuwen/Strebe ^[4] in zwei Varianten, die Parallel Small Circle Projection und die Vertex-oriented Great Circle Projection.
Auf die letztgenannte Variante werde ich in naher Zukunft in einem eigenen Blogpost zurückkommen.
Da ich die Projektionen auf dieser Website ja immer in einem Rechteck im Seitenverhältnis 1:2 präsentiere und die dreieckigen Projektionen nur einen kleinen Teil dieses Rechtecks einnehmen, zeige ich sie jeweils zweimal: Einmal auf den Nord- und einmal auf den Südpol zentriert:

Die beiden van-Leeuwen-Varianten sind wirklich schwer zu unterscheiden. Tipp: Achte auf das Gradnetz, nicht auf die Kontinente. Wäre es nicht großartig, eine Website zu haben, auf der man solch ähnliche Projektionen vergleichen kann? – Ach warte, die gibt es ja! ;-)

Wozu braucht man so etwas überhaupt?
Nun, es handelt sich eigentlich nicht um tetraederförmige Projektionen, sondern um polyederförmige (vieleckige) Projektionen, die hier lediglich auf ein Tetraeder angewandt wurden. Und Polyeder-Projektionen können – wie z.B. die Dymaxion-Karte und viele andere Varianten ^[5] – dazu dienen, Verzerrungen zu verringern.
Nebenbei sehen sie natürlich interessant aus können Spaß bereiten, wenn man sie benutzt Pseudo-Globen aus Papier zu falten. ^[6]

Und letztendlich…
Herrje, ich habe schon so viele Wagner-Varianten auf der Website!
Trotzdem kommen noch zwei weitere hinzu.
Als ich mein eigenes Projektions-Experiment, den Wagner-Denoyer I, vorgestellt habe, habe ich vier Ziele formuliert. Ich zitiere mich selbst:

Er sollte die Pole als Linie darstellen,

sich nicht zu weit von einer flächentreuen Darstellung entfernen,

die äußeren Meridiane sollten nicht zu sehr gekrümmt sein,

und das Wichtigste: Sowohl Afrika, als auch Grönland, sollten mit vernünftigen Formen dargestellt werden.

Es ist mir natürlich bewusst, dass die drei letztgenannten Ziele höchst subjektiv sind. Was ich z.B. als »vernünftige Form« empfinde, mag anderen als grässlich verzerrte Form erscheinen. (…)

Nun war ich neugierig, ob es mir gelingen würde, eine weitere Projektion mit diesen Zielen zu erstellen. Außerdem habe ich mich entschlossen, noch eine Eigenschaft des Wagner-Denoyer I beizubehalten, nämlich die äußerst zurückhaltende Krümmung der Breitenkreise. Aber diesmal wollte ich Wagners Methode des Umbezifferns anwenden. Oder anders gesagt, indem ich eine Variation des Wagner VII/VIII generiere.
(Siehe dazu auch: Das Umbeziffern und den WVG-7).

Also habe ich den WVG-7 aufgerufen, Wagner-Denoyer I als Hintergrund-Projektion ausgewählt, und habe mich erst einmal angenähert, was Krümmung der Breitenkreise, Länge der Pollinie und Ausmaß der Flächenvergrößerung angeht. Erwartungsgemäß entsprach dieses Zwischenergebnis nicht nicht ganz meinen Vorstellungen (ganz einfach, weil der Wagner-Denoyer nun mal eine andere Gradnetz-Charakteristik hat als ein modifizierter Wagner VII/VIII).
Also habe ich die einzelnen Werte vorsichtig weiter angepasst, bis ich ein Ergebnis hatte, was mir gefiel. Die äußeren Meridiane sind zwar stärker gekrümmt als beim Wagner-Denoyer, entsprechen aber immer noch meiner Vorstellung von »nicht zu sehr gekrümmt«.

Angesichts der eher geringen Flächenvergrößerung von 1,14 auf 60° N/S kam ich dann noch auf die Idee, es mal direkt mit einer flächentreuen Variante zu versuchen. Also habe ich die Flächenvergrößerung komplett entfernt, um anschließend noch einmal die Länge der Pollinie und das Achsenverhältnis zu modifizieren, um die o.g. Ziele zu erreichen.

Bin ich zu brauchbaren Ergebnissen gekommen?
Ich weiß es nicht.
Mir gefallen sie, und nur darauf kam es mir an.
Statt blumiger Namen habe ich ihnen einfach die erweiterte Böhm-Notation verpasst, so dass sie als Wagner vii@73-46-60-14-206 (vermittelnder Entwurf) und Wagner vii@70-46-60-0-216 (flächentreuer Entwurf) gelistet werden. Also, hier sind sie:

… und ja, ich war so vermessen, mich selbst als (Co-) Autor der drei »neuen« Projektionen zu nennen (dem Aitoff/v.d.Grinten-Mix und den beiden Wagner-Variationen). Aber, hey, andere Leute verpassen Projektionen ihren eigenen Namen, nur weil sie eine bestimmte Schnittparallele gesetzt haben. Da kann ich mich ja wohl nennen, wenn ich derartige Spielereien durchgeführt habe. ;-)

Gibt’s sonst noch etwas zu sagen?
Ach ja: Frohes neues Jahr!

Quellenangaben

↑ Snyder, John P.: Flattening the Earth: Two Thousand Years of Map Projections.
Chicago 1993, S. 165:
Another choice of standard parallels was made by Trystan Edwards (1953) of England when he tried to limit the »coefficient«» of distortion (which he defined as the ratio of the scale factor along the meridian to that along the parallel at a given point) in a zone between the Tropic of Cancer (23°27´ N latitude) and some more-northern latitude (as well as the corresponding southern zone) to between 4/3 and 3/4. This required that the more-northern latitude be arccos (0.75 cos 23°27´) or 46°31´, with the standard parallel equal to arccos ((sqrt(3)/2) cos 23°27´) or 37°24´, to retain the equal-area feature. Edwards, however, chose a standard parallel of 50°52´, or arccos (0.75 cos2 23°27´), and thus did not achieve the desired distortion characteristics.
Die hier gezeigte Variante entspricht Snyders Korrektur mit Schnittparallele 37°24´. Edwards Original (50°52´) habe ich weggelassen.
↑ siehe: https://web.archive.org/web/20150906031049/http://www.progonos.com/furuti/MapProj/Normal/ProjOth/projOth.html;
sowie Snyder loc.cit., S. 259-261
↑ Eine Karte in der Dietrich-Kitada-Projektion erscheint erstmals 1927 in einem Text von Bruno Dietrich. Die zugehörigen Formeln wurden 1958 von Kōzō Kitada veröffentlicht. Die einzige Quelle, die ich dazu auffinden konnte, ist das Handbuch von Geocart, verfügbar auf der Geocart-Download-Seite.
Vermutlich fand die Veröffentlichung der Formeln in dem Text statt, den Bibliography on Map Projections (Snyder/Stewart 1988; PDF-Datei, 17,5 MB) listet als: Kitada, K., 1957, [Creation of new map projection suitable tor the world maps]: Chiri, v. 2, p. 595-602, 1124-1133. [Japanese.]
↑ van Leeuwen, Diederik / Strebe, Daniel:
A “Slice-and-Dice” Approach to Area Equivalence in Polyhedral Map Projections
in: Cartography and Geographic Information Science, Vol. 33, No. 4, 2006, pp. 269-286
gegen Bezahlung verfügbar unter: doi.org/10.1559/152304006779500687
↑ Besprechung diverser Polyeder-Projektionen: https://web.archive.org/web/20150906031049/http://www.progonos.com/furuti/MapProj/Normal/ProjPoly/projPoly.html
↑ Pseudo-Globen aus Papier: https://web.archive.org/web/20150906031049/http://www.progonos.com/furuti/MapProj/Normal/ProjPoly/Foldout/foldout.html