Spilhaus-Projektionen: Ein Quintett von Weltmeer-Karten

Di, 26.4.2022 Spilhaus-Projektionen: Ein Quintett von Weltmeer-Karten

Heute habe ich fünf Projektionen hinzugefügt, die einzigartig sein dürften.
Die meisten Entwürfe in meiner Projektions-Kollektion zielen explizit oder implizit darauf ab, die Landflächen der Erde möglichst gut, d.h. mit geringen Verzerrungen, darzustellen. In dieser Hinsicht unterscheiden sich die Entwürfe von Athelstan F. Spilhaus (1911-1998), einem Geophysiker und Meeresforscher, grundsätzlich von allen anderen, die ich bisher gezeigt habe, denn sie konzentrieren sich auf die Darstellung der Ozeane.

Ja, ich habe einmal, quasi im Vorübergehen, die ozeanische Ansicht von Goodes Homolosine erwähnt. Hier wie dort erleiden die Landflächen das Schicksal, was üblicherweise den Ozeanen blüht: Sie werden an den Rand gedrängt, extrem verzerrt und unterbrochen.
Schaut mal, wie Euch das gefällt, Ihr Kontinente! 😉
Was die Spilhaus-Projektionen trotzdem einzigartig macht, ist die Tatsache, dass sie die Meere und Ozeane als einzige, ununterbrochene Wasserfläche darstellen.
Um den Autor selbst zu zitieren:^[1]

That the world ocean is a continuous body of water with relatively free interchange between its parts is of fundamental importance to oceanography. On ordinary world maps the interruptions forming the edges of the map are often placed in the oceans to show the continents to best advantage. If, on the other hand, oceanographic conditions as a whole are to be shown, it is desirable to have the map interrupted within the land masses and the world ocean shown as a unit.

Die Tatsache, dass das Weltmeer ein zusammenhängender Wasserkörper mit relativ freiem Austausch zwischen seinen Teilen ist, ist für die Ozeanographie von grundlegender Bedeutung. Auf gewöhnlichen Weltkarten sind die Unterbrechungen, die die Ränder der Karte bilden, oft in den Ozeanen platziert, um die Kontinente optimal zu zeigen. Sollen dagegen die ozeanographischen Verhältnisse in ihrer Gesamtheit dargestellt werden, so ist es wünschenswert, dass die Karte innerhalb der Landmassen unterbrochen und der Weltozean als Einheit dargestellt wird.

Aber bevor wir uns die Entwürfe ansehen, zunächst vier Hinweise:

Spilhaus hat keine neuen Projektionen entwickelt. Stattdessen verwendete existierende Entwürfe und wählte ein Kartenzentrum, welches dem gewünschten Zweck dienlich ist.
(Obwohl ihm das evtl. bei dem in diesem Blogpost letztgenannten Entwurf nicht bewusst war. Ich komme darauf zurück.)
Soweit ich das beurteilen kann, existieren keine etablierten Namen für die ersten vier Projektionen und nur ein »halb-etablierter« für die letzte. Daher habe ich die hier aufgeführten Namen, welche die ursprünglichen Schöpfer würdigen sollen, selbst ausgesucht. Aber ich werde auch alternative Bezeichnungen aufführen, die auf dem halb-etablierten Namen basieren.
(Und wenn ich mich jetzt zu kompliziert ausgedrückt habe: Einfach weiterlesen, die Sache wird schon klar werden.)
Die ersten beiden Projektionen sollten im Hochformat gezeigt werden, so wie ich es hier auch tue. Aus technischen Gründen wurden sie nebenan in meiner Projektions-Kollektion im 90° gegen den Uhrzeigersinn gedreht.
Drei Karten werden hier mit Wiederholung bestimmter Erdteile gezeigt. In der Projektions-Kollektion wird hingegen die Basiskarte, wie sie das Projektionsprogramm liefert, gelistet – also ohne Wiederholungen.

Hey Ho. Let’s go!

1942: Zwei Projektionen im Hochformat

1942 präsentierte Spilhaus erstmalig zwei Karten mit einem Projektionszentrum, bei dem das Weltmeer in den Fokus gestellt wird.

Spilhaus-Hammer I
oder
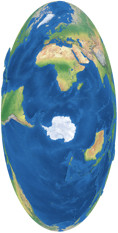
Spilhaus Weltmeer-Karte in einer Ellipse

Eine davon ist seine oben gezeigte Version der flächentreuen Hammer-Projektion. Als Zentrum verwendete er 70°Süd/15°Ost, bei einer Rotation der Achse um 90° gegen den Uhrzeigersinn (dem transversalen Aspekt).

Während diese Karte schon wunderbar zeigt, dass die fünf (oder drei oder sieben; je nachdem, welche Zählweise man bevorzugt) Ozeane, die wir üblicherweise benennten, eigentlich ein einziges, zusammenhängendes Gewässer darstellen, wird das Weltmeer nicht vollständig ohne Unterbrechungen gezeigt. Dies kann man bei bei obigen Karte leicht übersehen, wird aber deutlicher bei Spilhaus’ zweiter Karte von 1942, einer Variante des winkeltreuen August Epicykloidal, welcher das gleiche Projektionszentrum verwendet:

Spilhaus-August
oder
Spilhaus Weltmeer-Karte in einer Epizykloide

Hier ist eindeutig zu erkennen, dass vor allem der Golf von Mexiko, aber auch andere Randbereiche, unterbrochen werden: Die winkeltreue Projektion vergrößert die Randgebiete der Karte erheblich, während sie im flächentreuen Spilhaus-Hammer I in Ost-West-Richtung stark zusammengedrückt werden. Die fraglichen Gebiete werden natürlich vollständig gezeigt, sind aber abgeschnitten vom durchgängigen Weltmeer. Um dies auszugleichen, fügte Spilhaus seinen Karten ein paar Erweiterungen hinzu, ungefähr wie hier gezeigt:

Beim Spilhaus-August ist es offensichtlich, dass die Erweiterungen absichtlich hinzugefügt wurden. Beim Spilhaus-Hammer I hingegen sind so so klein, dass sie zumindest auf den ersten Blick wie Berechnungs-Fehler wirken. Darüber hinaus braucht man ein bisschen grafisches Geschick, um zu sie einzubauen (über welches ich nicht verfüge, deshalb sehen sie ein bisschen merkwürdig aus) und eine Projektionssoftware, die überhaupt in der Lage ist, einen Entwurf über seine Begrenzungen hinaus auszudehnen.

Wie man sehen kann, konnte ich sei zwar erzeugen, aber die dabei verwendete Software zeichnet die Erweiterungen in grauenhafter Qualität. Zum Glück wird das größtenteils dadurch verborgen, dass ich die Grafiken auf eine web-taugliche Größte runterskaliert habe, aber für eine gedruckte Karte wären sie absolut untauglich.

Im Hinblick darauf, dass sie als »Karten für das gesamte Weltmeer« gedacht sind, bin ich der Meinung, dass es noch Raum für Verbesserungen gibt. Vielleicht hat Spilhaus das gleiche gedacht, denn lange Zeit später später kam er auf dieses Thema zurück. Springen wir mal fast vierzig Jahre weiter.

1983: Zwei kreisförmige Projektionen

1983 stellte Spilhaus fünf weitere Weltmeer-Karten vor;^[2] zwei davon sehen wir uns an. Abermals griff er auf bestehende Projektionen zurück, abermals wählte er einen flächen- und einen winkeltreuen Entwurf, abermals verwendete er für beide das gleiche Projektionszentrum. Diesmal ist es 45°Süd/95°West.

Spilhaus-Lambert Azimutal
oder
Flächentreue Spilhaus Weltmeer-Karte in einem Kreis

Die Flächentreue Azimutalprojektion von Johann Lambert, zentriert auf die o.g. Koordinaten, zeigt das gesamte Weltmeer ohne jegliche Unterbrechungen. Sie hat ein dem Globus ähnliches Erscheinungbild, obgleich die Verzerrungen nicht den perspektivischen auf einem echten Globus entsprechen. Asien wird aufgeschnitten und gestreckt und umgibt so den Rest der Welt. Um die Eigenschaft der Flächentreue beizubehalten, muss der Kontinent in der Breite reduziert werden und erscheint im Ergebnis wie eine schmale, unauffällige Umrandung der Karte. Das Gleiche passiert aber auch mit Teilen des Weltmeeres, so dass sie kaum noch erkennbar sind – etwa das Mittel- und das Rote Meer. Wegen der Verzerrung der Küstenlinien fällt es überdies schwer, gewisse Bereiche des Meeres zu lokalisieren; etwa den Golf von Bengalen und das Arabische Meer.

Ich betone dies, weil es sich in der winkeltreuen Karte ganz anders darstellt:

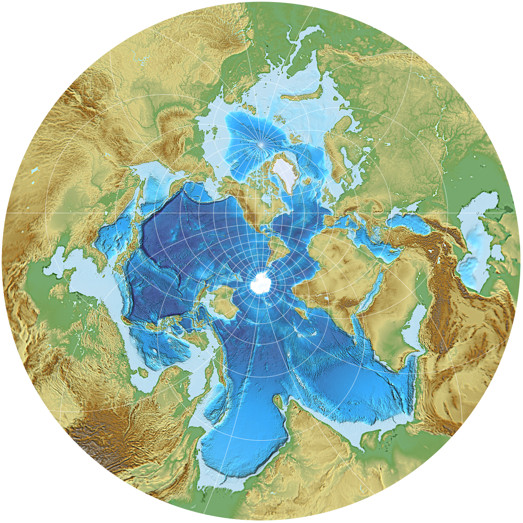
Spilhaus Stereographisch
oder
Winkeltreue Spilhaus Weltmeer-Karte in einem Kreis

Hier wird Asien vergrößert, und zwar ordentlich: Bei Sri Lanka wird die 100-fache Vergrößerung überschritten, und am äußeren Rand des Kreises beträgt der Wert Flächenvergrößerung 900. Ich bin mir ziemlich sicher, dass es ungeübten Kartenlesern schwerfällt nachzuvollziehen, was hier vorgeht. Möglicherweise nehmen sie sogar an, dass es sich um eine eine fehlerhafte Darstellung der Erde handelt. Andererseits könnte dies das Bewusstsein dafür schärfen, dass jede Kartenprojektion bis zu einem gewissen Grad willkürlich ist, und so dabei helfen, verbreitete Missverständnisse auszuräumen (z. B. die Vorstellung, es gäbe so etwas wie eine »genaueste« Projektion). Na gut, vielleicht ist dies eine gewagte Hoffnung…
Wie auch immer: In Bezug auf das erklärte Ziel der Karte – dazulegen, dass die Ozeane tatsächlich eine zusammenhängende Wasserfläche darstellen – mag diese Karte u.U. sogar besser sein als die vorhergehenden Ergebnisse.

Jahre später hat Spilhaus in seinem »Atlas of the World with Geophysical Boundaries«^[3] noch eine andere Variante dieser Karte gezeigt, in welcher nämlich die meisten Landflächen von Eurasien entfernt wurden. Er entschied sich für einen harten Schnitt an der Küstenlinie, für die Darstellung hier habe ich allerdings ein weiches »Ausblenden« gewählt:

Der Vollständigkeit halber sei noch darauf hingewiesen, dass auch die kreisförmige Version von Spilhaus’ stereographischer Karte nicht die komplette Erde darstellt: Da die Flächenvergrößerung der stereographischen Projektion zum Rand hin bis ins Unendliche wächst, muss sie begrenzt werden. Für die Darstellung hier habe ich mich entschieden, die Begrenzung bei dem Kleinkreis mit einem Radius von 159° um den Kartenmittelpunkt vorzunehmen. Bei diesem Wert werden nur Landmassen abgeschnitten, was für eine Weltmeer-Karte akzeptabel ist.
In der folgenden Grafik zeigt der schwarze Punkt, welcher Bereich nicht dargestellt wird:

1979: Eine quadratische Projektion

Springen wir noch einmal ein paar Jahren zurück, um die Projektion zusehen, welche meiner Meinung nach die faszinierendste der Reihe darstellt. Und tatsächlich handelt es sich auch um den Entwurf, der den Stein ins Rollen brachte, denn meine Aufmerksamkeit wurde auf Spielhaus’ Weltmeer-Karten gelenkt, als ich die ArcGis-Story von Šavrič, Burrows & Kennedy^[4] gelesen habe, in der sie sich mit dieser wundervollen Karte beschäftigen:

Spilhaus-Adams
oder
Spilhaus Weltmeer-Karte in einem Quadrat

Die drei Autoren stellen klar, dass diese Projektion 1979^[5] vorgestellt wurde (nicht 1942, wie manchmal behauptet wird) und zeigen, dass es sich dabei mit an Sicherheit grenzender Wahrscheinlichkeit um eine Variante von Adams konformer Erde in einem Quadrat II handelt, mit einem Projektionszentrum auf 49.56371678° Süd, 66.94970198° Ost, bei einer Rotation der Achse um 40.17823482° (oder, wenn du diese Schreibweise vorziehst, 49°33′49.3804″S, 66°56′58.9271″O und 40°10′41.6454″), welche nach Projektion um 45° im Uhrzeigersinn gedreht wurde.^[6]

Wie beim stereographischen Spilhaus ergibt sich das Problem – oder die Chance; je nachdem, wie man es sieht –, dass die Karte zunächst sehr verwirrend wirkt und die Flächenvergrößerung in Teilen der Karte ins Vieltausendfache anwächst. Darüber hinaus wiederholt sich das von Spilhaus-Hammer I und Spilhaus-August bekannte Ärgernis, dass das Weltmeer mit kleinen Unterbrechungen dargestellt wird (abermals am prominentesten im Golf von Mexiko).

Es gibt aber eine Lösung für beide Probleme. In Bezug auf die Unterbrechungen greifen wir abermals auf Wiederholungen zurück. Und diesmal brauchen wir nicht einmal eine Projektionssoftware, die Netzentwürfe über ihre Begrenzung hinaus ausdehnen kann. Diese Projektion kann nämlich gekachelt werden, d.h. man legt mehrere Kopien der Karte (zum Teil rotiert) nebeneinander, so dass sie ein durchgehendes »Mosaik« bilden. Dann schneidet man den Teil, den man benötigt, aus: In diesem Fall ein Rechteck ohne Unterbrechungen des Weltmeers, aber mit einigen Wiederholungen. Die Ergebnisse der beiden Schritte:

Du musst nicht unbedingt die gesamte Basis-Karte kopieren – es reicht natürlich auch, nur die benötigten Bereiche vom einen Kartenrand zu kopieren und am richtigen anderen Rand einfügen. Was immer Dir einfacher erscheint.

Aber was ist mit diesen gigantischen Vergrößerungen? Nun, die sind ausschließlich auf den Landflächen zu finden, und wir wollen ja eine Weltmeer-Karte. Wir löschen also einfach wieder die am stärksten vergrößerten Teile des Landes, wir brauchen sie nicht. Und dann landet man bei einer Variante des Spilhaus-Adams, die so aussieht:

Spilhaus-Adams mit Wiederholungen und gelöschten Landflächen

In dieser Konfiguration war der Entwurf im deutsche Magazin mare (siehe dieses Foto auf flickr, von Cédric Hüsler) und diversen anderen Publikationen zu sehen; John Nelson zeigt einige wunderschöne Karten in seinem Blogpost Spilhaus? More like Thrillhaus. Die finale Karte ist natürlich kein Quadrat mehr – nicht einmal, bevor man die Landflächen ausradiert hat. Nichtsdestoweniger ist der Namenszusatz »in einem Quadrat« korrekt, da die zugrundeliegende Projektion quadratisch ist.

Ich möchte noch ein Wort verlieren über die Bezeichnung, die ich gewählt habe, Spilhaus-Adams. Es ist seltsam: In allen Karten, die er vorstellt hat, hat Spilhaus den Original Autor genannt. Aber in diesem Falle hat er angegeben, es handele sich um »eine neue Projektion der Welt in einem Quadrat, entwickelt von den Geodäten Robert Hanson und Erwin Schmid, die mir mit den Gleichungen ausgeholfen und die Computer, welche die Karten zeichneten, programmiert haben« (zitiert nach Šavrič, Burrows, Kennedy). Haben sie Adams konforme Erde in einem Quadrat II neu erfunden? Derartige Sachen sind in der Welt der Kartenprojektionen schon passiert. Haben Hanson und Schmid vergessen zu erwähnen, dass die Gleichungen nicht von ihnen selbst entwickelt worden sind? Wir werden es wohl nie erfahren; aber nun, da wir annehmen können, dass es sich tatsächlich um die Adams-Projektion handelt (und meine Variante oben und die aus der ArcGis-Story defintiv schiefachsige Ansichten davon sind), ist der Name angemessen.

Fazit

Wir haben uns fünf der Weltmeer-Karten von Athelstan Spilhaus angesehen (er hat in seinem o.g. »Atlas of the World with Geophysical Boundaries« noch mehrere weitere gezeigt). Alle eignen sich hervorragend für Karten, welche den Ozean in den Fokus rücken sollen. Spilhaus-Hammer I und Spilhaus-August sind dabei vermutlich jene, auf denen sich auch ungeübte Kartennutzer am schnellsten orientieren können, aber die karten benötigen Erweiterungen, um den Ozean ohne jegliche Unterbrechungen darstellen zu können (was ein technisches Problem darstellen kann, je nachdem, welche Kartenprojektionssoftware man verwendet). Die globus-ähnliche Anmutung von Spilhaus-Lambert Azimutal mag Verwirrung verhindern, erschwert aber andererseits, gewisse Bereiche des Weltmeeres zu lokalisieren. Die fällt auf dem Spilhaus Stereographisch viel einfacher, auf dem aber wiederum die erdrückenden Landmassen abschrecken mögen. Man kann sie, wie gezeigt, löschen – es bleiben aber enorme Vergrößerungen auch auf der Fläche des Meeres (Arktischer Ozean, Golf von Bengalen).

Du merkst vermutlich schon, worauf ich hinaus möchte: Spilhaus-Adams ist mein Favorit! 😁
Damit meine ich die – von Spilhaus selbst übrigens nicht gezeigte – Version mit den entfernten Landflächen. Ja, auch dieser Entwurf mag auf den ersten Blick verwirrend wirken, aber ich denke, nach einem Moment fällt es nicht allzu schwer, alle Teile des Weltmeeres zu identifizieren, und die gräßlichsten Verzerrungen auf der Meeresfläche werden auch vermieden. Die Wiederholungen, die benötigt werden, um einen ununterbrochenen Ozean zu zeigen, können leicht hinzugefügt werden und benötigen keine speziellen Funktionen der Projektionssoftware.
In meinen Augen erfüllt sie das Ziel einer Weltmeer-Karte am besten.

Irgendwann in Kürze (hoffentlich) komme ich noch einmal auf das Thema von speziellen Ansichten älterer Projektionen und Kachelung zurück.

Quellenangaben / Fußnoten

↑ Spilhaus, A. (1942): “Maps of the whole world ocean.” Geographical Review, 32 (3), S. 431-435.
doi: 10.2307/210385 (Zugang nur mit Bezahlung)
↑ Spilhaus, A. (1983): “World ocean maps: The proper places to interrupt.” Proceedings of the American Philosophical Society, 127 (1), S. 50–60
jstor.org/stable/210385 (freier Zugang nach Registrierung)
↑ Spilhaus, A. (1991). “Atlas of the World with Geophysical Boundaries: Showing Oceans, Continents and Tectonic Plates in Their Entirety”. Independence Square, Philadelphia: The American Philosophical Society.
Einsehbar auf Google Books
↑ Bojan Šavrič, David Burrows, Melita Kennedy (2020): The Spilhaus World Ocean Map in a Square (engl.)
↑ Spilhaus, A. (November 1979). “To see the oceans, slice up the land.” Smithsonian, S. 54–63.
↑ Lies die Abhandlung von Šavrič, Burrows & Kennedy, um zu erfahren, wie sie auf dieses genau Projektionszentrum gekommen sind. Beachte auch, dass Spilhaus selbst höchstwahrscheinlich nicht mit dieser hohen Genauigkeit gerechnet hat: Acht Nachkommastellen in den Koordinaten bedeutet etwa einen Millimeter Unterschied in den Breitengraden.

Permalink

Kommentare

Sei der erste, der einen Kommentar hinterlässt!

Verbleibende Zeichen: 2048

Die folgenden vier Felder auf keinen Fall ausfüllen!

Nach oben

Projektiv.