Zwei Ginzburg- und vier Baranyi-Projektionen

Mo, 26.9.2022 Zwei Ginzburg- und vier Baranyi-Projektionen

Ich habe sechs Entwürfe in meine Projektions-Kollektion aufgenommen. Zwei sind einer bestehenden Projektion sehr ähnlich, vier sind eigenständiger. Bevor ich über sie spreche, kannst du schon mal einen Blick auf sie werfen:

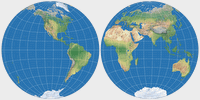
Ginzburg I & Ginzburg II

Die beiden azimutalen Ginzburg-Projektionen sind einander sehr ähnlich, also handeln wir sie gemeinsam ab.

Meine einzige Quelle über die zwei azimutalen Projektionen von Ginzburg ist Furutis^[1] kurzer Absatz über sie, also kann ich ihn auch einfach zitieren:

In 1949, Russian Georgiy A.Ginzburg proposed two azimuthal projections for hemispheres in school maps. Since Lambert’s equal-area projection compresses distances from the center of the map, causing considerable shape distortion near the borders, Ginzburg added a power term to Lambert's equations, slightly expanding the map. The result is neither conformal nor equivalent.

1949 schlug der russische Georgiy A. Ginzburg zwei azimutale Projektionen für Hemisphären in Schulkarten vor. Da die flächentreue Projektion von Lambert die Entfernungen vom Zentrum der Karte komprimiert, was zu erheblichen Formverzerrungen in der Nähe der Ränder führt, fügte Ginzburg den Gleichungen von Lambert eine Potenz hinzu, welche die Karte leicht vergrößert. Das Ergebnis ist weder winkel- noch flächentreu.

Bei einer derartigen Ähnlichkeit ist es sinnvoll, die Projektionen direkt miteinander zu vergleichen:
Flächentreue Azimutalprojektion vs. Ginzburg I
Flächentreue Azimutalprojektion vs. Ginzburg II
Ginzburg I vs. Ginzburg II

Bei der Beurteilung der Ergebnisse bin ich ein wenig zwiegespalten. Einerseits könnte man sagen: Die Abweichung von der Flächentreue ist gering genug, um keine falschen Vorstellungen von den Größenverhältnissen der Länder und Kontinente zu vermitteln, dafür erzielt eine Formverbesserung an den Rändern der Karten. Die Modifikation wäre dann also vorteilhaft. Andererseits könnte man aber auch sagen: Die Verbesserung der Formen ist so marginal, dass es sich nicht lohnt, dafür von der Eigenschaft der Flächentreue abzurücken.

Ich tendiere dazu, der letztgenannten Einschätzung zuzustimmen, obgleich der zusätzliche Platz an den Rändern, den die Ginzburg-Projektionen bieten, nützlich sein könnte, wenn man die Karte beschriften will.
Na ja… dies ist ohnehin eine eher akademische Frage, denn Hemisphären-Karten werden heutzutage kaum noch benutzt.

Hier noch die Darstellung der tissotschen Indikatrix, und dann kommen wir zu einer Art von Projektionen, wie man sie viel häufiger sieht.

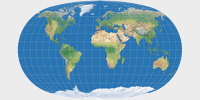
Baranyi I bis IV

1968 hat János Baranyi aus Ungarn sieben Projektionen vorgestellt, welche wie die beliebte Robinson-Projektion nicht mit mathematischen Formeln, sondern auf Grundlage von tabellarischen Koordinaten entwickelt wurden. Ich habe die originale Publikation nie gelesen, aber ich vermute, dass sie (abermals wie Robinson) auf eine ausbalancierte Darstellung der Erde abzielen. Daher sind sie weder flächen- noch winkeltreu. Ich hatte einige Zweifel, wie ich sie einordnen soll, denn erfahrenere Geister als ich haben sie bei der pseudozylindrischen^[2] Gruppe von Projektionen einsortiert^[3], allerdings entsprechen nur Baranyi I und II der strengen Definition^[4] des Begriffs. Letztlich habe ich mich entschieden, der strengen Definition zu folgen.

Leider konnte ich nur vier von ihnen in meine Projektions-Kollektion aufnehmen, weil ich keine Software habe, die alle sieben erzeugen kann. Das ist bedauerlich, weil mein Favorit unter denjenigen ist, die ich nicht hinzufügen konnte. 😕
Aber sehen wir sie uns genauer an.

🌐

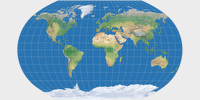
Baranyi I ist eine echte pseudozylindrische Projektion (oder eine echte unecht-zylindrische, wie es eigentlich heißen müsste 😉) mit Pol-Linie. Der Abstand zwischen den Breitenkreisen wächst vom Äquator zum Pol hin. Der Entwurf zeigt eine gewisse Ähnlichkeit zum Kavraiskiy VII, aber im direkten Vergleichen werden die Unterschiede schnell deutlich. Ganz grob würde ich sagen, dass ich Kavraiskiy VII in Bezug auf die Flächenverhältnisse vorziehe.

🌐

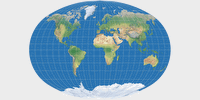
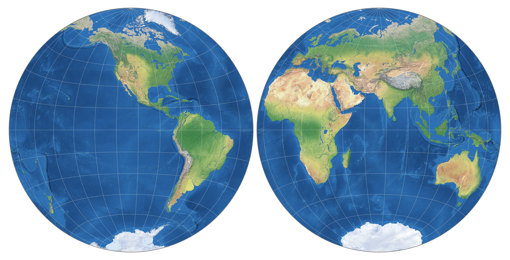
Baranyi II ist eine echte pseudozylindrische Projektion mit punktförmigen Polen, abermals wächst der Abstand der Breitenkreise, je weiter man sich vom Äquator entfernt. Und auch hier gibt eine grob ähnliche Projektion, nämlich Fahey – vergleiche sie miteinander. Wie üblich, führen die punktförmigen Pole zu einer besseren Darstellung der Formen in den hohen Breitengraden nahe des Zentralmeridians, aber umgekehrt zu stärkeren Verzerrungen nahe der äußeren Meridiane. Ich finde die äußere Form der Projektion ansprechend, aber das Ausmaß der Flächenvergrößerungen ist schon beträchtlich. Daher würde ich ich Projektion eher für dekorative Zwecke empfehlen.

🌐

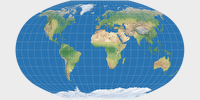
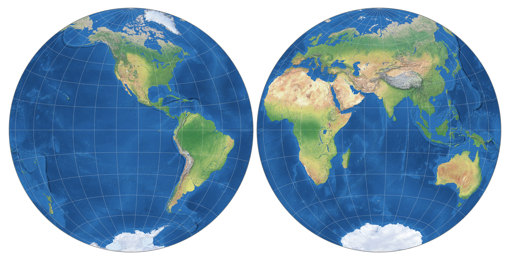
Baranyi III ist – genau wie die, die unten noch folgen – keine pseudozylindrische Projektion gemäss der strengen Definition: Die Abstände der Meridiane entlang eines gegebenen Breitenkreises nehmen vom Zentralmeridian zur äußeren Begrenzung leicht ab. Der Abstand der Breitenkreise zueinander wächst vom Äquator ausgehend zunächst an, um dann (ab ca. 50°N/S) wieder zu schrumpfen. Die Vergrößerung der polaren Gebiete fällt daher deutlich geringer aus als bei Baranyi I und II. Eine vergleichsweise kurze Pollinie – ein Drittel der Länge des Äquators – sorgt zudem dafür, dass sie auch in Ost-West-Richtung nicht allzu sehr gestreckt werden.

Dadurch fällt die die Winkelverzerrung in den höheren Breiten nahe der begrenzenden Meridiane im Vergleich zu Baranyi I zwar deutlich höher aus; nichtsdestoweniger kann ich sagen, dass ich diese Projektion den ersten beiden vorziehe, denn alles in allem erscheint mir die Verteilung der Verzerrungen ausgewogener zu sein.

🌐

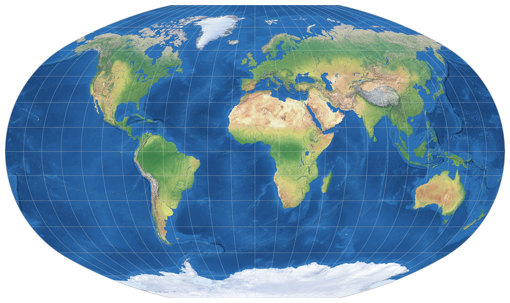
Baranyi IV ist eine Projektion mit punktförmigen Polen und einer interessanten Kombinationen von Eigenschaften: Sie hat deutlich sichtbare Scheitelpunkte (anders als z.B. Natural Earth II, welche auf den ersten Blick für eine Projektion mit Pol-Linien gehalten werden könnte); sie vermeidet die Schiefschnittigkeit der äußeren Längen in den höheren Breiten (anders als z.B. Apian II); sie hält die Flächenvergrößerungen geringer als die o.g. Baranyi II und Fahey. Dies ist eine äußerst seltene Kombination.

Ich finde, es handelt sich um einen sehr schönen, ääähhm… »pseudo-pseudozylindrischen« Entwurf, auch wenn die Flächenvergrößerung für meinen Geschmack ruhig noch etwas niedriger ausfallen dürfte. Ich kann mich nicht entscheiden, ob mir III oder IV besser gefällt; beide haben ihre Vor- und Nachteile. Generell nehme ich aber ein, dass eine punktpolige Projektion eher Akzeptanz findet als eine mit kurzer Pollinie. Vielleicht basiert diese Annahme auf der Tatsache, dass ich Baranyi IV tatsächlich in einem gedruckten Atlas gesehen habe, wo der Entwurf für die beiden doppelseitigen Haupt-Weltkarten (physische und politische Übersicht) verwendet wurde.^[5]

Hier ist die tissotsche Indikatrix für Baranyi I bis IV:

🌐

Ich habe leider kein Programm, mit dem ich die für meine Projektions-Kollektion nötigen Darstellungen von Baranyi V, VI und VII erzeugen könnte. Aber dank Anderson’s Gallery of Map Projections kann ich Euch wenigstens zeigen, wie sie aussehen:

Baranyi V und VI (beide mit punktförmigen Polen) zeigen eine sehr ungewöhnliche Eigenheit: Die gebogenen Meridiane werden bei etwa 75°N/S zu geraden Linien. Soweit ich ich das auf den Grafiken erkennen kann, besteht die Verbindung zwischen dem Pol und ≈75° bei der Projektion V aus zwei Liniensegmenten, bei VI hingegen aus einer einzigen Strecke. Ich muss zugeben, dass diese Eigenheit meinen Augen ziemlich missfällt. Baranyi V zeigt abermals »wachsende und schrumpfende« Abstände der Breitenkreise (wie III & IV); bei Baranyi VI wachsen die Abstände über die gesamte Strecke (wie bei I & II).

Baranyi VII is die einzige Projektion der sieben, bei der die Abstände der Breitenkreise vom Äquator zu den Polen durchgängig schrumpfen. Daher fallen die Flächenvergrößerungen geringer aus als bei den anderen sechs – was den Entwurf zu meinem Favoriten der Baranyi-Projektionen macht! Allerdings habe ich das Gefühl: Wenn man die Gesamtverzerrungen messen würde (z.B. unter Verwendung des Airy-Kavraiskiy-Kriteriums), käme Baranyi IV zu einem besseren Ergebnis als VII.
Aber zum Glück muss mich das ja nicht kümmern. 😉

Genug gequasselt.

Quellenangaben / Fußnoten

↑ Zitiert nach Carlos Furutis Website aus dem Internet-Archiv.
↑ An dieser Stelle möchte ich noch einmal darauf hinweisen, dass der Begriff pseudozylindrisch in der deutschsprachigen Fachliteratur eigentlich nicht zu finden ist, stattdessen werden die fraglichen Projektionen als unecht-zylindrisch bezeichnet. Für meine Website und diesen Blog habe ich mich aber vor Jahren entschlossen, den deutschen Begriff an den englischen (pseudocylindric) und französischen (pseudo-cylindrique) anzupassen.
↑ Alle Baranyi-Projektionen werden als Pseudozylinder gelistet im libproj4-Handbuch von Gerald I. Evenden, der Map Projection Gallery von Paul B. Anderson, der List of Map Projections von G.Projector, und in ihrer Erwähnung bei der Beschreibung der Robinson-Projektion im Handbuch von Geocart. In Flattening the Earth, führt John P. Snyder sie mit den Worten »nicht-flächentreue pseudozylinder-ähnliche Projektionen« ein (S. 216), um sie in der Tabelle auf S. 281 bei den Pseudozylindern aufzulisten.
↑ Die strenge Definition des Begriffs »pseudozylindrisch« (oder »unecht-zylindrisch«, s.o.) ist z.B. in der englischen Wikipedia (… die Meridiane sind entlang jedes Breitenkreises gleich weit voneinander entfernt) oder in daan Strebes Map Projection Essentials (siehe Abschnitt »Mathematical projection«) zu finden: Projektionen mit zu den Polen hin gekrümmten Meridianen und geraden, maßstabsinvarianten Breitenkreisen (der Maßstab eines gegebenen Breitenkreises ist über seine gesamte Länge konstant).
↑ Diercke Drei Universalatlas, Westermann Schulbuchverlag GmbH, 1. Auflage 2001.