Die Danseiji-Projektionen

Mo, 14.6.2021 Die Danseiji-Projektionen

Die Danseiji-Projektionen – /dɑnˈseɪdʒi/; von den japanischen Wörtern 弾性 (dansei, “Elastizität”) and 地 (chi, “Erde”) – wurden im November 2019 von Justin Kunimune vorgestellt.^[1]
Sie sind einmalig: Während drei von ihnen recht konventionell aussehen (und vier tun dies nicht), sind sie anders konstruiert als jede mir bekannte existierende Projektion. Ich denke, ich kann das nicht besser erklären als @Fil dies getan hat, also zitiere ich ihn einfach:

Instead of the traditional approach, where an elegant mathematical formula describes the mapping between spherical and planar coordinates, the idea with these projections is to create a mesh on the sphere, and map the mesh to the plane by assigning a position to each of the vertices. The mapping could be prepared manually, or through some kind of finite elements algorithm, designed to optimize for arbitrary constraints. For example, one might want to favor land continuity, or to lower the distortion of areas, or angles – or any other rule such as giving a larger amount of space to land vs ocean, or a larger amount of space to more populated areas…

Anstelle des traditionellen Ansatzes, bei dem eine elegante mathematische Formel die Abbildung zwischen Kugel- und Ebenenkoordinaten beschreibt, besteht die Idee bei diesen Projektionen darin, ein Netz auf der Kugel zu erstellen und das Netz auf die Ebene abzubilden, indem jedem der Schnittpunkte eine Position zugewiesen wird. Die Abbildung kann manuell erfolgen oder durch eine Art Finite-Elemente-Algorithmus, der für die Optimierung beliebiger Bedingungen ausgelegt ist. Zum Beispiel könnte man die Kontinuität von Land bevorzugen oder die Verzerrung von Flächen oder Winkeln verringern – oder jede andere Regel, wie z.B. eine größere Fläche für Land gegenüber dem Ozean oder eine größere Fläche für stärker besiedelte Gebiete…

Hinweis: Wenn ich Kunimunes Abhandlung richtig verstehe, wird das Ursprungs-Netz nicht auf der Kugel erstellt, sondern auf einer existierenden Projektion, nämlich – im Falle von Kunimunes unten gezeigten Beispielen – der Hammer-Projektion bzw. der mittabstandstreuen Azimutalprojektion. Das spielt keine große Rolle, aber ich wollte es trotzdem erwähnen.

Mit diesem Ansatz erreichen man eine Gestaltungsfreiheit, die mit formelbasierten Projektionen nicht oder nur mit sehr hohem Aufwand erreicht werden kann, aber man kann sich auch auf Projektionen beschränken, die eher traditionell aussehen.
Sehen wir uns also Kunimunes Vorschläge an – da die ersten drei einige Ähnlichkeiten haben, betrachten wir sie in einem Block; die restlichen vier werden dann separat behandelt.

Danseiji N, Danseiji I, Danseiji II

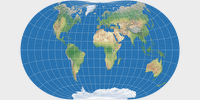
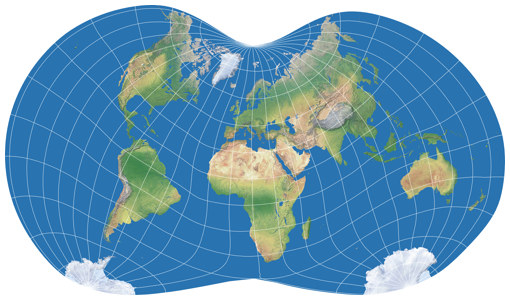
Der Danseiji N ist ein ziemlich »normaler« Entwurf für Weltkarten, nichts was einen gelegentlichen Kartennutzer verwirren würde. Es handelt sich um eine aphylaktische oder vermittelnde Projektion mit einer eher geringen Flächenvergrößerung. In Bezug auf die Verzerrungen vergleicht Kunimune ihn mit Winkel Tripel, Robinson und Wagner VIII, und ja, man kann sagen, dass sie in der gleichen Liga spielen. Genau wie diese drei ist Danseiji N in meinen Augen sehr gut für allgemein-geografische Weltkarten geeignet – aber im Gegensatz zu diesen verfügt er über punktförmige Pole, was realistischer ist und u.a. zu einer besseren Form von Grönland führt. Wer eine aphylaktische punktpolige^[2] Projektion sucht, findet hier einen guten Kandidaten.

Danseiji I ist eine flächentreue Projektion – nun, beinahe.
Mathematisch gesehen, zeigt sie einige Abweichungen von der Äquivalenz, aber für das menschliche Auge sind diese nicht zu sehen – man könnte es also einen »in jeder praktischen Hinsicht flächentreuen« Entwurf nennen. Davon abgesehen, ist er dem Danseiji N sehr ähnlich.
Ich habe lange darüber nachgedacht, ob ich ihn in der Liste auf meiner Website als vermittelnde Projektion aufführen soll, nebst Hinweis, dass er nahezu flächentreu ist – oder umgekehrt als flächentreue Projektion mit dem Hinweis, dass er genau genommen nicht flächentreu ist. Ich habe mich für letzteres entschieden: Das ist zwar weniger genau, aber in Hinsicht auf Vergleiche von Projektionen ist das in meinen Augen sinnvoller.

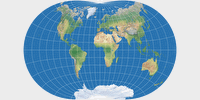
Danseiji II ist dem Danseiji N ebenfalls sehr ähnlich, geht aber in die entgegengesetzte Richtung, mit einer stärkeren Flächenvergrößerung, wodurch die Darstellung der Formen verbessert wird – und erledigt die Aufgabe, Winkelverzerrungen klein zu halten, tatsächlich sehr gut. Für meinen persönlichen Geschmack fallen die Flächenverzerrungen aber schon ein wenig zu hoch aus. Andererseits sagt Kunimune: »Es wäre eine gute Projektion für große Poster«, und wenn man bedenkt, dass viele Wandkarten entweder die Mercator-Projektion oder van der Grinten I verwenden, dann muss ich sagen, dass Danseiji II in dieser Hinsicht tatsächlich eine Verbesserung wäre. Bedauerlicherweise muss ich aber bezweifeln, dass die Kartenhersteller dies als angemessene Alternative ansehen, denn ich glaube, dass sie rechteckige Projektionen bevorzugen. Mercator ist ohnehin rechteckig, und van der Grinten I kann – wie ich vor einiger Zeit ausgeführt habe – leicht zu einer rechteckigen Karte gewandelt werden; eine Vorgehensweise, die eigentlich auch auf den Danseiji II angewandt werden könnte, aber mit weniger überzeugenden Resultaten.

Bisher hatten wir drei Projektionen. Ich mag ihre subtile Variante der Form, die ich mittlerweile »telophasisch« nenne. Mir gefällt auch die Idee einer Familie an ähnlich aussehenden Projektionen, von denen eine (nahezu) flächentreu ist und die anderen beiden ein ansteigendes Ausmaß an Flächenvergrößerungen zeigen – ganz ähnlich wie z.B. Wagner VII, VIII und IX.
Was mir weniger gefällt, ist die extreme Nord-Süd-Streckung der niedrigen Breiten. Die ist ein typisches Problem von flächentreuen Entwürfen mit Pol-Linie, aber hier haben wir eine flächentreue Projektion mit punktförmigen Polen und zwei vermittelnde. Insofern würde es leichter fallen, das Problem zu vermeiden. Kunimune kritisiert die Hammer-Projektion und den Strebe 1995 da sie beide »die äußeren Längengrade zu stark strecken«. Ich nehme an, er hat versucht, dieses zu vermeiden (und zwar mit Erfolg!) – aber meiner Meinung nach ist der Preis dafür zu hoch.

Hier ein kleines Experiment – Danseiji I, horizontal gestreckt um einen Faktor von 1,06 und (um die Eigenschaft der Quasi-Flächentreue beizubehalten) gleichzeitig vertikal gestaucht um ≈0,943 (den Kehrwert von 1,06):

Ja, das bringt die starke Streckung der äußeren Längengrade zurück; und höchstwahrscheinlich vermindert es die vorteilhaften Werte der Winkelverzerrung. Aber visuell empfinde ich diese Version als ausgeglichener.

Aber bevor mich mich zu tief in persönliche Vorlieben stürze, gehen wir lieber zu den verbleibenden vier Projektionen über, welche alle sehr ungewöhnlich und daher interessanter sind.

Danseiji III – Danseiji VI

Anders als die ersten drei Projektionen, welche sich bemühen, die Verzerrungen über die gesamte Karte zu reduzieren, konzentriert sich Danseiji III ausschließlich auf die Landmassen, um die Verzerrungen so weit wie möglich in die Ozeane werfen – die einzige Art der Verklappung, die ich begrüße! Wie Du sehen kannst, verwirft der Entwurf auch jegliche Idee von Symmetrie und Regelmäßigkeit. Und erreicht tatsächlich sehr niedrige Verzerrungen auf Landflächen. Wieder einmal (wie bei den Canters-Projektionen) zeige ich eine Darstellung der Tissotschen Indikatrix nur auf Land, um Ablenkung durch die Verzerrungen im Meer oder die Außenform der Karte zu vermeiden:

Obwohl der Entwurf nicht flächentreu ist (auch nicht beinahe flächentreu wie Danseiji I), muss man sich die Tissot-Ellipsen schon sehr genau ansehen, um die Abweichung der der Äquivalenz zu erspähen. Die Winkelverzerrungen sind leichter auszumachen, bleiben aber trotzdem noch sehr moderat. (Ich spreche hier nur von der Verzerrungen an Land!) Antarktika wird zwar in zweigeteilt, aber die beiden Teile werden deutlich geringer verzerrt als in den meisten anderen Projektionen. Und das »Layout« der Kontinente bleibt sehr nahe am gewohnten Bild.
Kunimune sagt: »Ich denke, dies ist die am weitesten verwendbare Danseiji-Projektion«, und da stimme ich absolut zu. Es ist eine sehr gute Kartenprojektion für sehr viele Anwendungsgebiete.

Das einzige Problem ist, dass – soweit ich das beurteilen kann – asymmetrische Projektionen allgemein nicht so gern gesehen sind, was ich sehr bedauerlich finde.

Übrigens – es gibt eine frühere Projektion, die eine gewisse Ähnlichkeit zum Danseiji III hat. Ich rede von Halstead’s Composite World interrupted projection. Ich habe sie nur ein einziges Mal gesehen, nämlich auf Carlos Furutis hervorragender Kartenprojektions-Website, die höchst bedauerlicherweise aus dem Web verschwunden ist, aber wenigstens kann man sie noch in der The Wayback Machine lesen (zum Ende der Seite scrollen). Leider wurde nur das kleine Vorschaubild erhalten. Wie die Danseiji-Projektion hält sie die meisten Verzerrungen vom Land fern, um ihnen in den Ozeanen freien Lauf zu lassen; darüber hinaus zeigt sie eine vergleichbare Anordnung der Kontinente. Ich selbst bevorzuge das »sauberere« Gradnetz der Composite World; als Nachteile vermerke ich allerdings, dass sie nicht ohne Unterbrechungen auskommt, eine riesige Lücke im Europäischen Nordmeer und dem Nordatlantik erzeugt – und ihr Grönland ist nicht halb so hübsch wie im Danseiji III.
Unterm Strich bevorzuge ich Kunimunes Projektion, aber Halsteads Arbeit ist auf jeden Fall eine Erwähnung wert. Es ist wirklich schade, dass es (abgesehen von dem verlinkten bisschen) im Web keinerlei Informationen über diese Projektion gibt.

🌐

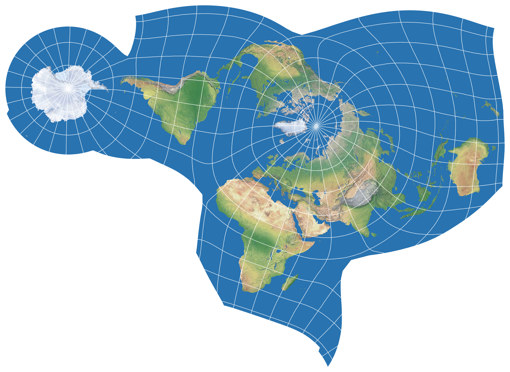
Wie die Nummer III, konzentriert sich der Danseiji IV auf die Landflächen, wobei er sich aber noch weiter von konventionellen Karten entfernt: Er wechselt von der äquatorständigen zur polaren Ansicht und erlaubt einige Unterbrechungen, wodurch die Verzerrungen weiter verringert werden. Es gibt noch gewissen Größenverzerrungen, jedoch… nun, vielleicht ist Dein Augenmaß besser als meins, aber für mich ist es nahezu unmöglich zu sagen, wo sie sind – abermals sind die Winkelverzerrungen leichter zu finden, obgleich sie sehr niedrig sind:

Obwohl sich die Begrenzungsschnitte und damit die äußeren Formen unterscheiden, so ist Danseiji IV doch einigermaßen vergleichbar zur Dymaxion-Karte, ich selbst finde die »organische« Form des Danseiji-Entwurfs aber ansprechender.
Und noch etwas: Wie Du wahrscheinlich bemerkt hast, haben die ersten beiden Karten oben eine andere Ausrichtung als die »Tissot an Land«-Grafik (welche die Ausrichtung zeigt, für die sich Justin Kunimune in seinen Dokumenten entschieden hat). Ich habe die Karte ein bisschen gedreht, damit sie besser in den Rahmen mit einem 2:1-Seitenverhältnis, den ich auf der Website immer benutze, passen. Und das zeigt eine weitere Stärke des Entwurfs: Du kannst ihn eigentlich drehen, wie Du willst, und erhältst immer eine brauchbare Karte. Selbstverständlich kann man jede Karten rotieren, aber bei den meisten Projektionen führen nur bestimmte Winkel zu einer brauchbaren Karte – eine Einschränkung, die meiner Meinung nach bei Danseiji IV nicht gegeben ist.

Also, wenn Du eine ungewöhnlich Karte mit sehr geringen Verzerrungen an Land haben möchtest oder benötigst – dies ist eine gute Wahl!
Dennoch ein kleiner Hinweis, in Bezug auf Kunimunes eigene Einschätzung der Projektion: »sie zeigt die Beziehungen zwischen den Kontinenten (besonders Nordamerika und Eurasien) wirklichkeitsgetreuer, als es jede lentikuläre Projektion könnte«. Während die relative Position der Kontinente auf der nördlichen Hemisphere sicherlich besser dargestellt wird als in den Karten, die wir gewohnt sind, trifft dies nicht unbedingt auf die südliche Hemisphäre zu. Darüber hinaus ist dies keine Folge davon »nicht lentikulär« zu sein, sondern eher vom Aspekt, nämlich dass Der Entwurf von einer Azimutalprojektion mit einem Projektions-Zentrum auf der nördlichen Hemisphäre abgeleitet wurde. Mit einem entsprechen Zentrum kann jede lentikuläre Projektion die relativen Positionen genauso gut abbilden – siehe unten, am Beispiel des Strebe 2011, wie ich ihn in meinem Kartenprojektions-Kalender von 2018 benutzt habe.
Aber das sind Haarspaltereien, Danseiji IV behandelt diese Angelegenheit gut, also spielt es keine große Rolle, warum das so ist.

Bisher hatten wir also drei eher konventionelle Projektionen, die auf eine vorteilhafte Verteilung der Verzerrungen über die gesamte Karte hinweg abzielen; und zwei ungewöhnliche Projektionen, bei denen niedrige Verzerrungen an Land das Ziel war, wobei – quasi als Nebeneffekt – hohe Verzerrungen in den Ozeanen erlaubt waren. Nun schauen wir uns zwei Projektionen an, die bestimmte Teile der Erde absichtlich mit Verzerrungen versehen. Was?!?
Klingt komisch, ist aber so. Und sogar aus gutem Grund.

🌐

Danseiji V sieht sehr merkwürdig und ungenau aus – was der Entwurf auch ist. Wie schon gesagt, fügt er absichtlich Verzerrungen hinzu: Er verkleinert die Ozeane. Aber warum?
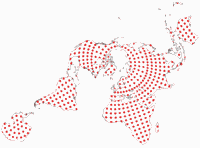
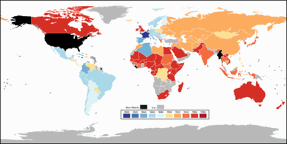
Wie Du wahrscheinlich weißt, bedecken die Ozeane etwa 70% der Erdoberfläche. Aber auf vielen thematischen und statistischen Karten braucht man die Ozeane eigentlich nicht. Sieh dir diese Beispiele einer Choroplethenkarte an, welche den Zeitraum der Metrikation (Prozess der Einführung des metrischen Systems) der Länder zeigen. Die erste verwendet die Rektangularprojektion für eine komplette Weltkarte. 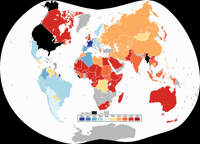Die zweite verwendet eine Variante des Wagner VIII und präsentiert eine häufig benutzte Technik, die auf Karten dieser Art angewandt wird, um Platz sparen, nämlich das Beschneiden der Karte. 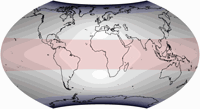Und die dritte zeigt Danseiji V:

Die drei oben gezeigten Karten basieren auf einem Original von NuclearVacuum & Carnby, CC BY-SA 3.0, via Wikimedia Commons

Der Leerraum der Ozeane vermittelt keine Informationen – es entsteht also kein Verlust durch die Verkleinerungen im Danseiji V. Die Kontinente aber behalten ihre gewohnte Form und Position, was für Karten dieser Art wichtig ist. Es gibt ein gewisses Ausmaß an Flächenvergrößerungen an Land, die meiner Meinung nach besser verteilt sein könnten; aber sie bleiben gering genug, um keinen großen Unterschied zu machen.

Für platzsparende statistische/thematische Karten, die sich nur auf Kontinentalbereiche beziehen (und idealerweise kein Gradnetz benötigen), halte ich die Herangehensweise des Danseiji V für viel besser als beschnittene Karte nach Art des oben gezeigten Wagner-Beispiels.
Da ich den Entwurf für keine Art von physischer Karte empfehlen würde, habe ich ihn hier mit einer politischen Darstellung vorgestellt. (Nebenan auf meiner Projektions-Liste musste ich natürlich eine physische Karte verwenden, weil es mein erklärtes Ziel ist, alle Projektionen in gleicher Darstellung aufzuführen.)

Das gleiche gilt auch für die letzte Projektion. Und wenn Du schon dachtest, dass Danseiji V merkwürdig aussieht, halt Dich fest…

🌐

Was soll das denn sein?
Vielleicht hast Du schon mal Kartogramme gesehen wie das von ourworldindata.org oder das von worldmapper.org, bei denen die Größe der Länder der Größe der Bevölkerungszahl entsprechen. Der Danseiji VI macht eigentlich das gleiche, allerdings mit zwei Unterschieden: Der Größenunterschied zwischen den am dichtesten und am wenigsten besiedelten Gebieten wurde reduziert und er bezieht sich auf die Bevölkerungszahl von Gebieten, nicht von Ländern. Daher werden z.B. einige Teile von China vergrößert, andere aber verkleinert. Das Resultat stellt einen Kompromiss zwischen einer Karte und einem Kartogramm dar, welcher Informationen nach Art eines Kartogramms vermittelt, aber alle Länder weiterhin an ihrer Form erkennbar sind wie auf einer Karte.

Visualisierung der Verzerrungen

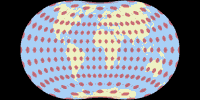
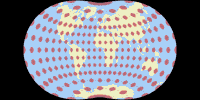
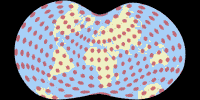
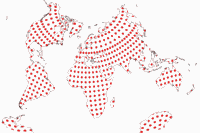
Für die Visualisierung der Verzerrungen habe ich Justin Kunimunes eigene Projektions-Software verwendet. Ich finde, die Grafiken sind nicht ganz einfach zu lesen – ganz besonders im Fall der Danseiji-Projektionen, bei denen die Verteilung der Verzerrungen aufgrund der Konstruktionsmethode recht unregelmäßig ausfällt. Nichtsdestoweniger sind sie hilfreich. Zu Vergleichszwecken zeige ich auch andere Projektionen, die oben erwähnt wurden: Robinson, Winkel Tripel und Wagner VIII (für den Vergleich mit Danseiji N); Equal Earth, Toblers Hyperelliptische und Strebe 1995 (für Danseiji I) und die Dymaxion-Karte (für Danseiji IV).

Blaue Bereiche zeigen Flächenvergrößerungen an, rote Bereich Verkleinerungen. Graue Bereiche stehen für Winkelverzerrungen. Dunklere Farbtöne weisen höhere Verzerrungswerte auf.

Fazit

Justin Kunimune hat eine neue Methode, um Kartenprojektionen zu erstellen, vorgestellt und ihre Anwendung an sieben Projektionen demonstriert. Danseiji N, I und II sind nicht gerade spektakulär – weil sie es nicht sein sollen, sie wurden als Alternative zu konventionellen Projektionen entworfen. Sie haben realistische punktförmige Pole und die leicht telophasische Form erzeugt ein angenehmes Erscheinungsbild. Meiner eigenen Meinung nach würden sie alle von einer moderaten horizontalen Streckung profitieren – aber das kann man ja selbst machen, entweder durch Eingabe von entsprechenden width/height-Werten im Export-Dialog von Kunimunes oben erwähnter eigener Software, oder einfach durch die Verwendung eines Grafikprogramms.

Danseiji III ist ein Entwurf mit erfreulich geringen Flächen- und Winkelverzerrungen der Landmassen. Seine Form ist ungewöhnlich, die Anordnung der Kontinente macht ihn aber trotzdem tauglich für viele Anwendungszwecke. Die Unregelmäßigkeiten im Gradnetz empfinde ich – rein ästhetisch gesehen – störender als die doppelte Asymmetrie. Tja nun … ein bisschen Schwund ist immer, gerade bei Kartenprojektionen. 😉

Danseiji IV hat sogar noch geringere Verzerrungen an Land, dürfte für die meisten praktischen Anwendungen aber zu ungewöhnlich sein. Der Urheber selbst empfiehlt den Entwurf »für alle Anwendungen, für die heute die Dymaxion-Projektion benutzt wird, also künstlerische Darstellungen und Karten zur Ausbreitung des Menschen« – eine Empfehlung, der ich vollauf zustimmen kann.

Danseiji V hat das Potential, für viele thematische Karten verwendet zu werden – ich würde den Entwurf gerne häufig in entsprechender Anwendung sehen. Und Danseiji VI… nun, es muss sich noch zeigen, ob solche Hybride angenommen werden. Ich muss zugeben, dass ich da ein bisschen skeptisch bin.

Bezüglich Kunimunes neuer Konstruktionsmethode – er hat bewiesen, dass sie sowohl für konventionelle, als auch für ungewöhnliche Projektionen verwendet werden kann; obgleich ich denke, sie spielt ihre Stärken bei unregelmäßigen, asymmetrischen Entwürfen aus. Kunimune stellt die technischen Details und Sourcecode zur Verfügung (lies den Vorabdruck seiner Abhandlung), so dass sich jeder da einarbeiten kann. Es wird spannend sein zu sehen, ob auch andere Leute diesen Ansatz nutzen werden, um neue Projektionen zu kreieren…

Quellenangaben

↑ Justin Kunimune: Introducing the Danseiji Projections (engl.)
Der Link führt zu Justins Blogpost, der wiederum einen Verweis zu seiner kostenpflichtigem wissenschaftlichen Abhandlung und einer frei verfügbaren Pre-Print-Version enthält.
↑ Ich glaube nicht, dass irgendjemand außer Dr. Böhm und mir jemals das Wort »punktpolig« benutzt hat. Es ist aber hilfreich, wenn man nicht ständig die Umschreibung »mit punktförmigen Polen« benutzten möchte… 😉

Permalink