Ein flächentreuer Entwurf nach Art der AuthaGraph-Karte

Mo, 15.1.2018 Ein flächentreuer Entwurf nach Art der AuthaGraph-Karte

Aktualisiert: Mi, 27.6.2018

Hinweise auf Justin Kunimunes Approximation eingefügt..

Seitdem die AuthaGraph-Weltkarte von Hajime Narukawa im Oktober 2016 den japanischen Good Design Grand Award gewonnen hat, hat sie jede Menge Aufmerksamkeit geerntet – eine Liste einiger Artikel ist unten zu finden.^[1] Leider sind die meisten dieser Artikel voll von Missverständnissen, Ungenauigkeiten und schlichtweg falschen Behauptungen.
Aber das ist heute nicht das Thema. Darüber werde ich mich irgendwann in (hoffentlich) nicht allzu ferner Zukunft auslassen. Im Moment möchte ich nur in aller Kürze ein paar Dinge festhalten:

– Nein, die AuthaGraph-Karte ist nicht die »genaueste Weltkarte, die es gibt«. Es gibt keine genaueste Weltkarte, und es wird nie eine geben.

– Nein, die AuthaGraph-Karte ist nicht einmal genauer als die Mercator-Projektion. Sie vermeidet die extremen Verzerrung der Größenverhältnisse, das ist richtig. Aber das allein macht keine Karte »genauer« als irgendeine andere.

– Nein, die Mercator-Projektion lügt nicht und sie ist auch nicht fehlerhaft. Sie wurde für einen speziellen Zweck geschaffen, nämlich alle Loxodrome als Geraden zu zeigen. Die Aufgabe erfüllt sie exakt (sie ist sogar die einzig mögliche Projektion, welche im Stande ist, dies zu leisten). Eine Lüge ist höchstens die Behauptung, wir alle würden immer nur die Mercator-Projektion zu sehen bekommen, wenn wir eine Weltkarte betrachten.
Glaubt mir das nicht einfach – geht in die nächste Buchhandlung und studiert die Weltkarten der dort ausliegenden Atlanten. Es würde mich wundern, wenn Ihr auch nur einen Atlas findet, welcher für die Haupt-Weltkarten den Mercator verwendet.

– Nein, die AuthaGraph-Karte ist nicht flächentreu, d.h. sie zeigt nicht die wahren Größenverhältnisse. Die Urheber der Karte behaupten das auch nicht, diverse Artikel tun dies aber schon. Und ehrlich gesagt – der Name AuthaGraph, dessen erster Teil erklärtermaßen von authalic (= flächentreu) abgeleitet ist, trägt nicht gerade dazu bei, dieses Missverständnis aufzuklären.
Ist sie der Flächentreue wenigstens nahe, wie die restlichen Artikel sagen? Nun, »nahe« ist natürlich ein sehr ungenauer Begriff. Unter den vermittelnden Kartennetzentwürfen gehört sie sicher zu jenen, die sich eher an der Flächen- denn an der Winkeltreue orientieren. Aber meiner Meinung nach sind die Abweichungen von der Flächentreue schon zu auffallend, um von echter Nähe zu sprechen.

– Nein, die Karte lässt sich nicht »in einen dreidimensionalen Globus zurückfalten«. Die Variante, mit der dies möglich ist (und die als Papiermodel angeboten wird), ist ein Zwischenschritt in der Konstruktion der Karte und nicht mit der fertigen Weltkarte identisch. (Und nebenbei bemerkt: Selbst wenn dies möglich wäre, würde da nur ein ziemlich mieser Globus bei rauskommen, denn das Falten von Papier beseitigt keine Verzerrungen.)

– Nein, die Karte eignet sich nicht, um Flugrouten zu ermitteln.

– Und Nein, Nein, Nein, die Karte löst mit Sicherheit kein »455 Jahre altes Problem«. Sie löst kein Problem, welches »jede Karte, die wir je gesehen haben geplagt hat«. Sie löst gar kein Problem. (Nun, höchstens ein Einkommens-Problem der Urheber, aber mit Sicherheit kein kartographisches Problem.)

Nachdem ich das nun gesagt habe, möchte ich betonen: Ich habe nichts gegen die AuthaGraph-Karte. Nur etwas gegen falsche Behauptungen. Tatsächlich mag ich die Karte selbst sogar! Ich mag alle ungewöhnlichen Kartenprojektionen. Denn auf jeden Fall erinnern sie uns daran, dass jede Projektion, so normal und gewöhnlich sie uns auch vorkommen mag, nichts weiter als eine bestimmte Interpretation darstellt – ein Versuch unter theoretisch unendlich vielen, mit dem Problem umzugehen, dass sie die (nahezu) kugelförmige Erdoberfläche nicht genau auf einer flachen Karte darstellen lässt.
Und von einem rein ästhetischen Gesichtspunkt finde ich die AuthaGraph-Karte durchaus ansprechend. Ihr praktischer Wert mag nicht der allergrößte sein – jedenfalls fallen mir auf Anhieb nicht allzu viele Zwecke ein, in denen sie anderen Projektionen überlegen wäre, außer vielleicht einem einzigen, sehr speziellen Fall, auf den ich im o.g. zukünftigen Artikel eingehen werde. Aber wer sagt, dass eine Weltkarte nicht auch einfach nur hübsch und ansprechend sein darf? Ich sicher nicht!

Nun gibt es aber ein weiteres Problem bei der AuthaGraph-Weltkarte: Selbst wenn Du sie für einen bestimmten Zweck einsetzen möchtest – Du kannst es gar nicht. Du kannst zwar ein fertiges Poster kaufen, aber Du kannst keine eigene Weltkarte mit dieser Projektion erzeugen. Denn die Formeln, mit denen die Karte erzeugt wird, sind nicht veröffentlicht worden, und daher kann sie auch in keins der gebräuchlichen Kartenprojektions-Programme eingebaut werden.

Aus diesem Grund hat sich schon Marcin Ciura ins Zeug geschmissen und eine Pseudo-AuthaGraph-Karte entworfen, inklusive Veröffentlichung der notwendigen Formeln.^[2] Das wusste ich nicht, als ich mit meinen eigenen Experimenten begonnen habe. Und da ein solches Unterfangen meine eigenen mathematischen Fähigkeiten bei weitem übersteigt, habe ich eine ganz andere Vorgehensweise gewählt: Ich habe mich für eine existierende Projektion entschieden, mit der sich Ergebnisse erzielen lassen, welche der AuthaGraph-Karte nicht ganz unähnlich sind.

Update 27.6.2018: Es war mir bisher nicht bekannt, aber es existiert eine weitere Annäherung an die AuthaGraph-Karte, kreiert von Justin Kunimune, die noch näher am Original ist. Siehe Update-Hinweis unten.

Die Vorgehensweise

Ich habe mich für die van-Leeuwen-Projektion (oder auch Vertex-oriented Great Circle Projection, wie sie die Autoren bei der Vorstellung^[3] genannt haben) entschieden, die sich – wie ich schon berichtet habe – dazu eignet, Pseudo-Globen in Form eines regelmäßigen Tetraeders zu konstruieren. Schließlich basiert auch die AuthaGraph-Karte auf dieser geometrischen Form. Darüber hinaus handelt es sich um einen flächentreuen Entwurf – denn es war mein erklärtes Ziel, zu einem Ergebnis zu kommen, welches tatsächlich (und nachweislich) der Flächentreue entspricht. Als Software kam Geocart zum Einsatz, welches meines Wissens das einzige Kartenprojektions-Programm ist, welches den van Leeuwen anbietet.

Die Arbeitsschritte an sich sind recht einfach.
1. Lege ein neue Karte mit der van-Leeuwen-Projektion an.

2. Wähle ein geeignetes Zentrum der Projektion aus, ggf. mit einer gewissen Achsenneigung.
(Auf die Auswahl eine geeigneten Zentrums komme ich noch zu sprechen.)

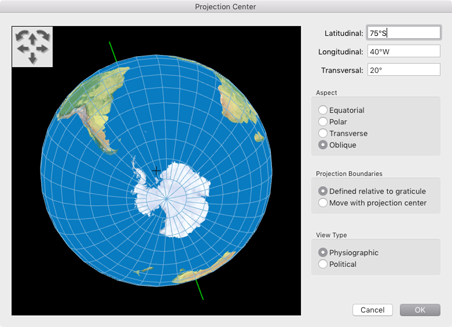
3. Dupliziere das Ergebnis, rotiere das Duplikat um 180 Grad.

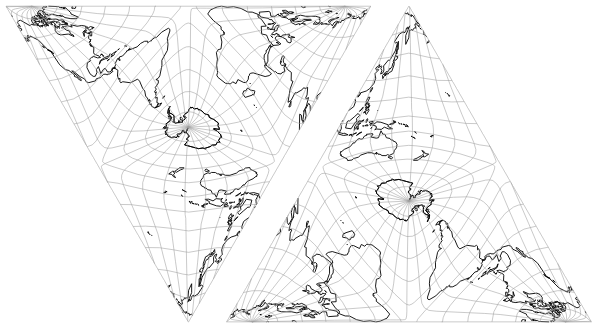
4. Füge die beiden Karten nahtlos zusammen.

Das nahtlose Zusammenfügen ist zugegebenermaßen ein Problem: Aus Gründen, die ich jetzt nicht näher ausführen werde, wird man die »Naht« immer sehen. Ich kann Dir nur empfehlen, es so zu machen wie ich: Behaupte einfach, es sei Absicht, dass man den Übergang sieht, damit der Betrachter immer noch nachvollziehen kann, wie die fertige Karte zusammengesetzt wurde! ;-)

5. Wiederhole das Duplizieren & Zusammenfügen so oft, wie Du es möchtest oder brauchst.

6. Nun hast Du eine gekachelte Darstellung. Wenn Du als Endergebnis eine rechteckige Karte haben willst, schneide das gewünschte Rechteck aus.

7. Fluche und schimpfe, weil das Rechteck entweder Landmassen durchtrennt, die Du zusammenhalten wolltest, oder gewisse Areale doppelt enthält. ;-)

8. Gehe zurück zu Schritt 2 und wähle ein neues Zentrum aus.

Abhängig davon, ob Du lieber in Geocart oder lieber in einem Grafikprogramm arbeitest, kannst Du den aktuellen Stand aus Geocart exportieren nach den Schritten 2, 3, 4 oder 5. Für Schritt Nr. 6 brauchst Du dann definitiv ein Grafikprogramm.

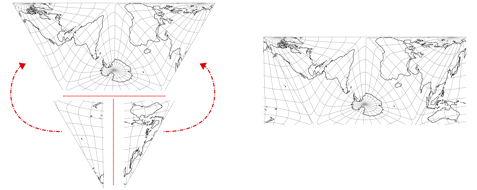
Außerdem gibt es noch eine alternative Herangehensweise, die darin besteht, die dreieckige Projektion nach Schritt 2 zu exportieren und sie im Grafikprogramm nach folgendem Schema zu zerschneiden und wieder zusammenzusetzen:

Für eine einzelne Karte ist dies wohl auch die bessere Vorgehensweise. Da ich aber etliche Projektionszentren durchprobiert habe, war es besser, mehrere Dreiecke in Geocart zusammenzusetzen und dann für das jeweilige Zentrum neu berechnen zu lassen.

Wie findet man denn nun ein geeignetes Projektionszentrum?
Du willst ja sicherlich nicht Dein restliches Leben damit verbringen, alle rechnerisch möglichen Kombinationen von Längen- und Breitengrad sowie Achsenneigung durchzuspielen…

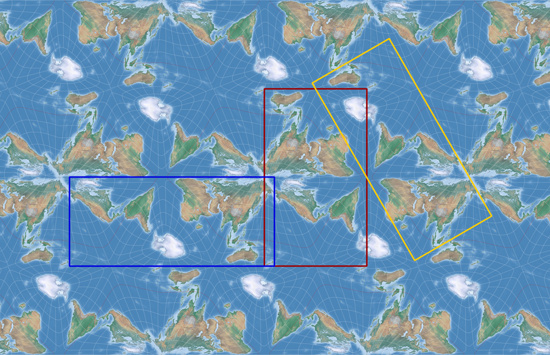
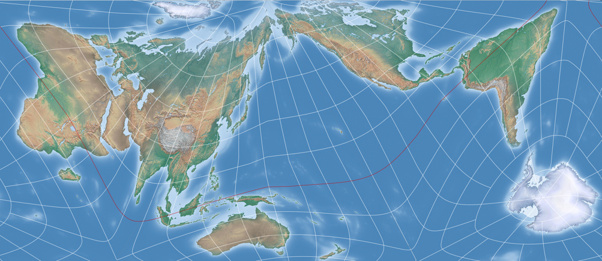
Am besten gehst Du natürlich geplant vor, die es Marcin Ciura in seinem Blogpost demonstriert hat. Ich selbst habe mich an dieser Planung vorbeigemogelt, indem ich AuthaGraph-Darstellungen wie Bild Nr. 2 auf dieser Seite [direkter Link auf das Bild] betrachtet und versucht habe, den Mittelpunkt zu erraten – gefolgt von eine Reihe von Versuch-und-Irrtum-Durchläufen.

Trotz dieser recht unwissenschaftlichen Vorgehensweise bin ich zu Ergebnissen gekommen, die ich zufriedenstellend finde. Bevor ich jetzt endlich dazu übergehe, Euch diese Ergebnisse zu präsentieren, möchte ich noch ein paar Sachen vorausschicken:

Meine Ergebnisse weisen durchweg höhere Winkelverzerrungen (= Verzerrungen der Formen) auf als das AuthaGraph-Original oder die Variante von Ciura und Kunimune. Das liegt vermutlich wenigstens zum Teil daran, dass meine Experimente flächentreu (und nicht nur »nahe der Flächentreue«) sind. Indes, wenn Du die Formverzerrungen der AuthaGraph-Karte bereits grenzwertig findest, lies hier besser gar nicht erst weiter – dann sind Marcin Ciuras und Justin Kunimunes Reproduktionen die bessere Lösung für Dich.
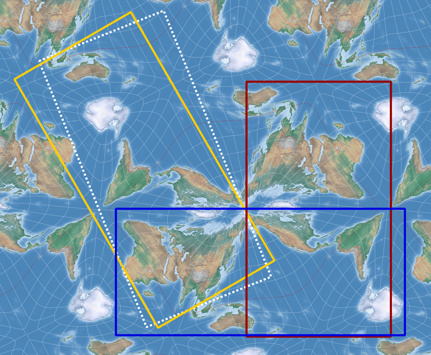
Die Möglichkeiten, eine rechteckige Karte ohne Unterbrechungen von Landmassen auszuschneiden, sind bei meinen Ergebnissen eher begrenzt. Andererseits ist auch die originale AuthaGraph-Karte in dieser Disziplin nicht so gut, wie gerne behauptet wird. Schau Dir noch einmal das oben verlinkte Bild an: Nur das grüne und das weiße Rechteck erfüllen diese Anforderung. Das rote, das orange und das gestrichelte Rechtecke durchtrennen Landmassen, wie meine Ergebnisse auch.
Ich behaupte keineswegs, dass ich die besten Möglichkeiten gefunden habe! Du kannst gerne selbst mit der van-Leeuwen-Projektion experimentieren – es ist absolut möglich, dass Du eine bessere Konfiguration findest.
Ich möchte hier keine verbesserte AuthaGraph-Karte vorschlagen.
Ich möchte die AuthaGraph-Karte nicht ersetzen.
Meine ursprüngliche Motivation war einfach der Spaß am Experiment, ob ich eine flächentreue Karte hinbekomme, die eine gewisse Ähnlichkeit aufweist.
Mehr nicht.
Dass diese Experimente andere Menschen in die Lage versetzen, eine eigene AuthaGraph-ähnliche Karte zu erstellen, ist ein positiver Nebeneffekt, war aber nicht mein Hauptziel.

Genug gequasselt!
Bekommen wir jetzt endlich Karten zu sehen?!?

Die Ergebnisse

Ich bin zu verschiedenen Ergebnissen gekommen, die alle ihre eigenen Vor- und Nachteile haben. Das erste Beispiel behandele ich zu Demonstrationszwecken ein wenig ausführlicher – die anderen werde ich dann schneller abhandeln.

Beispiel Nr. 1

Mein persönlicher Favorit unter den Experimenten wird erreicht, indem man das Projektionszentrum auf 75° Süd/40° West legt, bei einer Achsenneigung von 20°.
Das von Geocart erzeugte Resultat sieht folgendermaßen aus:

In der gekachelten Version suchen wir nun die geeigneten Schnittmarken, um rechteckige Karten auszuschneiden.
In horizontaler Richtung erlaubt diese Konfiguration leider nur eine Variante, die nicht durch Landmassen schneidet (im Gegensatz zum Original, welches drei Varianten ermöglicht). Der vertikale und der schräggestellte Schnitt durchtrennen ebenfalls Landmassen – aber auf ganz ähnliche Art und Weise wie das Original:

Sehen wir uns diese rechteckigen Karten in vergrößerter Version an!
Der horizontale Schnitt geht durch die Beringstraße und durchtrennt keine der großen Landmassen… naaajaaaa, da sind ein paar Pixel von Alaska und Neuseeland, die auf der jeweils anderen Seite der Karte landen. Aber wenn man den Schnitt zugunsten von Alaska versetzt, verschlechtert sich die Situation für Neuseeland und umgekehrt. Ich nehme mir also die Freiheit, die paar Pixel zu übersehen und nenne dieses hier mein Ergebnis:

Auch den vertikalen und den schrägen Schnitt sehen wir uns in groß an – das gekippte Rechteck habe ich hier wieder aufgerichtet. Wie oben gesagt, entsprechen diese Varianten ziemlich genau den originalen Beispielen der AuthaGraph-Karte.

Der Vollständigkeit halber sehen wir uns auch noch schnell die beiden anderen horizontalen Schnittmöglichkeiten an. Setzt man Afrika ganz nach links (so, wie in der am häufigsten gezeigten Variante der AuthaGraph der Fall ist), wird die Antarktis durchschnitten.
Setzt man Südamerika ganz nach rechts, wird die Antarktis ebenfalls geteilt, allerdings bleibt nur ein sehr kleiner Rest auf der rechten Seite der Karte übrig. Ich finde diesen kleinen Rest sogar etwas ärgerlicher als deutliche Trennung in der »Afrika-links«-Variante. Aber vielleicht empfindest Du das ja anders.

Bei diesem kleinen Antarktis-Rest, der rechts von Südamerika übrig bleibt, war es klar, dass es auch eine Variante geben muss, welche Südamerika und die Antarktis komplett voneinander trennt – also habe ich sie gesucht.

Beispiel Nr. 2

Im zweiten Beispiel (welches ich, wie versprochen, nun kürzer abhandle) habe ich das Projektionszentrum auf 76° Süd, 51°20´ West bei einer Neigung von 32° gelegt. Nun kann man Südamerika ganz nach rechts legen, ohne die Antarktis anschneiden zu müssen:

Auch ein Schnitt durch die Beringstraße ist möglich – ja, sogar noch »sauberer« als im ersten Beispiel:

Warum ist dies also nicht mein Favorit, sondern Beispiel 1?
Die Nachteile dieser Konfiguration liegen meiner Meinung nach darin, dass Afrika und Irland doch sehr nah an den Rand gequetscht werden – und Neuseeland wird, kaum merklich, sogar durchtrennt: Stewart Island erscheint, von den neuseeländischen Hauptinseln getrennt, am Kartenrand unterhalb der Antarktis.
Das sind natürlich minimale Nachteile gegenüber des ersten Beispiels. Aber dennoch gefällt mir die Nr. 1 ein bisschen besser.
Ein kleines bisschen.

Der vertikale und der schräge Schnitt bringen keine besonderen Änderungen im Vergleich zum ersten Beispiel, daher verzichte ich auf eine Darstellung und gehe direkt zum dritten Beispiel über.

Beispiel Nr. 3

Wie gesagt, sieht man die AuthaGraph-Karte meistens in der Variante, die Afrika am linken Bildrand platziert. Auch dafür habe ich eine Variante gefunden: Projektionszentrum 74° Süd, 10° Ost, Neigung -42°.

Leider erlaubt diese Konfiguration keine anderen vernünftigen Schnitte: Das vertikale und das gedrehte Rechteck haben mit ungünstigen Aufteilungen von Landmassen oder Wiederholungen zu kämpfen.

Das gestrichelte Rechteck erlaubt zwar einen einigermaßen brauchbaren schrägen Schnitt – allerdings werden einige Areale im Pazifik doppelt dargestellt, wie Du feststellen kannst, wenn Du das Gradnetz aufmerksam betrachtest. Das mag auf Karten ohne Gradnetz und/oder flacher Darstellung der Ozeane nicht einmal auffallen… es ist trotzdem etwas gemogelt. ;-)
Diese Variante würde von daher nur empfehlen, wenn man unbedingt Afrika ganz links und keinen Anschnitt der Antarktis haben möchte.

Die Nachahmung aufgeben

Wer sich nur für AuthaGraph-ähnliche Karten interessiert, kann den folgenden Abschnitt ignorieren und direkt zum Abschnitt über die Verzerrungen weiterspringen…

Ich habe es nämlich irgendwann verworfen, der AuthaGraph-Karte so ähnlich wie möglich zu werden – sowohl was die Optik, als auch was die Möglichkeit der (fast) beliebigen Schnitte angeht. Und ich finde, auch dabei kann man ansprechende Karten erstellen.

Beispiel Nr. 4 und 5

Bei der ersten handelt es sich um die Konfiguration 73°25´ Süd, 116° West, Neigung -34°. Mir gefällt das Resultat – es ist ein bisschen näher an Weltkarten, wie wir sie gewöhnt sind; und immerhin ermöglicht es noch, die Antarktis ganz nach links oder ganz nach rechts zu setzen, ohne andere Kontinente zu schneiden.

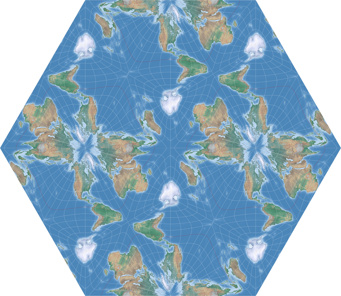
Ich finde diese Variante durchaus tauglich, wenn man eine rechteckige, flächentreue Weltkarte ohne Unterbrechungen der Kontinente haben möchte – sie macht sich allerdings auch recht gut zu rein dekorative Zwecken. Besonders gut gefällt mir hier die Anordnung in einem Sechseck:

Erst nachdem ich diese Variante erstellt hatte, ist mir aufgefallen, dass die Autoren bei der Vorstellung der Projektion ein ähnliches Beispiel aufgeführt haben. Das liegt daran, dass ihre Anordnung im Papier etwa so aussah:

Rekonstruktion der Darstellung im Papier von Strebe/van Leeuwen

Wenn man diese Konfiguration (meinen Versuchen zufolge müsste das 20°N/90°W ohne Achsenneigung sein) aber kachelt und anschließend rotiert, kann man folgendes Rechteck ausschneiden:

Das ist also tatsächlich meinem vorhergehenden Beispiel nicht ganz unähnlich, auch wenn hier Alaska durchtrennt wird. Die dekorative Darstellung im Sechseck hat zudem den Vorteil, dass die beiden Südamerikas etwas weiter voneinander abrücken:

Beispiel Nr. 6a und 6b (unfertige Studien)

Die letzten Beispiel würde ich zum gegenwärtigen Zeitpunkt noch als vorläufige Entwürfe bezeichnen. Sie bewegen sich noch näher an die Anordnung, wie wir sie von üblichen Weltkarten kennen – das mag man sowohl als Vor-, aber auch als Nachteil sehen. Das Gradnetz wird immer noch verbogen und verdreht, aber meiner Ansicht nach in einer – hmm, wie sag ich das? – nachvollziehbareren Weise als bei den obigen Beispielen. Die Antarktis muss leider aufgeteilt werden. Auf das Ausschneiden des Rechtecks im Hoch- und Schrägformat verzichte ich hier, denn das führt zu keinen brauchbaren Ergebnissen.
Wahrscheinlich werde ich irgendwann in näherer Zukunft mal ausprobieren, ob ich ausgehend von diesen Konfigurationen noch zu Weltkarten komme, die mir persönlich besser gefallen.

Hier also die beiden Ergebnisse mit den Projektionszentren 42° Süd/167° Ost (ohne Neigung) und 50°S/29°W/7,5°.

Das soll an Beispielen genügen.
Sehen wir uns nun die Verzerrungen in der Projektion etwas genauer an.

Verzerrungen

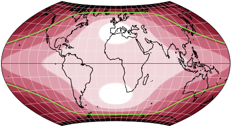
Dies ist kein Tapetenmuster aus den 1970er Jahren. Dies ist eine Visualisierung der Verzerrungen (oder auch eine univariate Farbdarstellung der Verzerrungseigenschaften, wie es im Geocart-Handbuch heißt) in der van-Leeuwen-Projektion – wir sprechen hier natürlich von Winkelverzerrungen (= Verzerrungen der Formen), denn bei einem echten flächentreuen Netzentwurf (habe ich erwähnt, dass die AuthaGraph-Karte von der Flächentreue abweicht?) gibt es ja keine Verzerrungen der Größenverhältnisse. Es spielt dabei keine Rolle, welches Projektionszentrum ausgewählt wurde – innerhalb des ursprünglichen Dreiecks ist die Verteilung der Verzerrungen immer gleich. Nur die Lage der Kontinente innerhalb des Dreiecks ändert sich, und rücken sie natürlich in unterschiedlich verzerrte Bereiche.
Wie liest man dieses Diagramm? Dabei hilft die folgende Legende:

Hellere Farbtöne bedeuten weniger Verzerrungen. Dunklere Farbtöne bedeuten mehr Verzerrung. Für dieses Diagramm habe ich eine Einstellung gewählt, bei der jede Farbschattierung einen Bereich von 10 Grad Winkelverzerrung abdeckt: Weiß steht für eine Winkelverzerrung von 0 bis 10 Grad, der hellste Rot-Ton für 10 bis 20 Grad, der nächste für 20 bis 30 Grad usw.
Auf die grünen Linien komme ich gleich zurück.

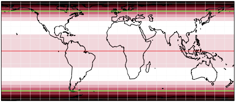
Wie Du sehen kannst, gibt es im Diagramm der van-Leeuwen-Projektion keine weißen Bereiche: Es gibt keinen Bereich auf der Karte, der frei von Verzerrungen ist. Das hast Du Dir beim Anblick der Karten wahrscheinlich schon gedacht. Es gibt da aber eine Sache, die ich sehr interessant finde. Um das zu verdeutlichen, zeige ich hier die Verzerrungs-Diagramme von drei flächentreuen Projektionen, die für ihre geringe Durchschnitts-Winkelverzerrung bekannt sind (Eckert IV, Wagner VII und Behrmanns flächentreuer Zylinderentwurf) sowie von einer Ausführung der Sinucyli-Projektion, um auch einen Entwurf mit punktförmigen Polen dabei zu haben:

Alle vier haben große Bereiche mit einer Winkelverzerrung von weniger als 20° – diese Bereiche fallen beim van Leeuwen eher klein aus. Aber alle vier haben auch Bereiche, welche den Wert von 100° überschreiten! Schauen wir uns nun auch die grünen Linien an: Sie markieren die Winkelverzerrung von genau 42°, welches der höchste ganzzahlige Wert innerhalb der van-Leeuwen-Projektion ist (das absolute Maximum liegt bei etwa 42,7°). Bei den anderen vier Projektionen liegen noch beachtlich große Bereiche jenseits dieses Wertes.

Hier ist noch einmal die Legende, die ich oben gezeigt habe – hier habe ich (ganz grob) den Bereich an Verzerrungswerten, der innerhalb des van Leeuwen auftritt, markiert. Die anderen Projektionen hingegen nutzen das gesamte Spektrum von 0 bis > 100.

In der van-Leeuwen-Projektion sind die Verzerrungen also gleichmäßiger verteilt. Nun, manchmal werden flächentreue Projektionen deshalb empfohlen, weil sie eine »gerechte« Darstellung der Erde ermöglichen: Kein Land wird bevorzugt, keins benachteiligt – alle werden in den korrekten Größenverhältnissen dargestellt. Aber wenn einem der Sinn danach steht, sollte sich diese Gerechtigkeit nicht auch auf das Ausmaß der Verzerrungen beziehen?
In der van-Leeuwen-Projektion werden alle Länder und Kontinente verzerrt dargestellt; manche mehr, manche weniger. Aber mit deutlich geringerer Varianz als bei üblichen Karten. Mir scheint das keine schlechte Idee zu sein, wenn es Dir um Gerechtigkeit der Darstellung geht.

Zur Klarstellung: Ich sage nicht, dass die Bemühung um Gerechtigkeit geboten ist. Diese Überlegung überlasse ich denjenigen, die eine Weltkarte erstellen wollen. Ich sage nur: Die »Gerechtigkeit der Darstellung« ausschließlich auf Größenverhältnisse zu beziehen, aber nicht auf Verzerrung der Formen, erscheint mir ein wenig inkonsequent.

So!
Nach diesem kleinen philosophischen Ausflug möchte ich aber auch noch die Darstellung der tissotschen Indikatrix und der univariaten Farbdarstellung der Verzerrungseigenschaften präsentieren, für alle der oben gezeigten Varianten (aber nur jeweils in einer Schnittvariante).

… und wie kann ich das nutzen?

Zeit für schlechte Nachrichten:
Meines Wissens ist Geocart die einzige Kartenprojektionssoftware, welche die van-Leeuwen-Projektion anbietet – und Geocart ist nicht gerade billig. (Meiner Meinung nach ist es seinen Preis wert, sonst hätte ich es nicht gekauft; aber ich kann nachvollziehen, wenn das zu teuer erscheint.)
Die Formeln sind schon 2006 veröffentlich worden, sind aber nur zugänglich, wenn man a) zufällig die fragliche Ausgabe der Zeitschrift Cartography and Geographic Information Science besitzt, oder b) den kostenpflichtigen Zugang auf tandfonline.com nutzen möchte.

Wie auch immer, die Formeln sind veröffentlich worden und sie selbst unterliegen keinem Copyright – es müsste sich also nur jemand mal die Mühe machen, sie abzuschreiben, und schon können sie überall veröffentlicht (und von allen entsprechenden Programmen verwendet) werden.

Zusammenfassung

Mein Ziel war es, einen flächentreuen Entwurf zu schaffen, welcher dem Erscheinungsbild der AuthaGraph-Karte nahekommt. Ist mir das gelungen?
Nun, auf den ersten Blick zeigen sich Ähnlichkeiten, was die Lage der Kontinente und die Verteilung der Winkelverzerrung angeht. Bei genauerer Betrachtung zeigen sich allerdings deutliche Unterschiede. Vor allem die stärkere Verzerrung der Formen mag bei diesen Experimenten unangenehm auffallen. Diese lassen sich, wenigstens zum Teil, aber wahrscheinlich durch die absolute Flächentreue erklären. Wer nach einer AuthaGraph-Alternative sucht, aber eher Wert auf möglichst große Formtreue legt, den weise ich nochmals auf die Ergebnisse von Marcin Ciura und Justin Kunimune hin.

In Bezug auf die Größenverhältnisse ist meine van-Leeuwen-Konstruktion aber genauer als die AuthaGraph-Karte. Hey, vielleicht sollte ich sie als »allergenaueste Karte der Welt« vermarkten? ;-)
Nein, denn die verbesserte Genauigkeit der Größen hat ja einen Preis, nämlich die erhöhte Winkelverzerrung. Darüber hinaus sie hier ja »nur« genauso genau wie jede andere (echte) flächentreue Projektion: Nämlich korrekt.

Vor allem aber hat die van-Leeuwen-Projektion den Vorteil, dass zumindest eine Software sie unterstützt und die zugehörigen Formeln veröffentlicht worden sind (zwar sind sie derzeit nur recht schwer zugänglich – s.o. –, aber das kann sich ändern). Und das ermöglicht es, eigene Karten zu erstellen und die Verzerrungen selbst zu studieren, anstatt sich auf ungenaue Angaben wie »beinahe korrekte Größenverhältnisse« zu verlassen.

Revolutionär, wegweisend oder in irgendeiner Weise »besser« oder gar »genauer« als andere Entwürfe, sind aber weder das Original, noch Ciuras oder Kunimunes Entwurf, noch mein Experimente.

Update 27.6.2018: Justin Kunimunes AuthaGraph-Approximation

Es war mir im Januar, als ich obigen Blogpost verfasst habe, nicht bekannt, aber schon zu diesem Zeitpunkt existierte eine weitere (nicht flächentreue) Annäherung an die AuthaGraph-Karte, welche dem Original deutlich näher kommt als Marcin Ciuras Variante:
Justin Kunimune präsentierte seinen englischsprachigen Artikel Reverse Engineering the AuthaGraph (Nachkonstruktion der AuthaGraph) bereits im November 2017. Die Formeln für seine Approximation sind enthalten im frei verfügbaren Quellcode von Kunimunes eigener Kartenprojektions-Software, welche darüber hinaus für Windows als eigenständiges Programm sowie für macOS und Linux als ausführbare Java-Dateien angeboten werden (für deren Ausführung eine Java-Runtime-Umgebung benötigt wird).

Ich werde in der (hoffentlich) nicht allzu fernen Zukunft genauer über diese Approximation berichten.
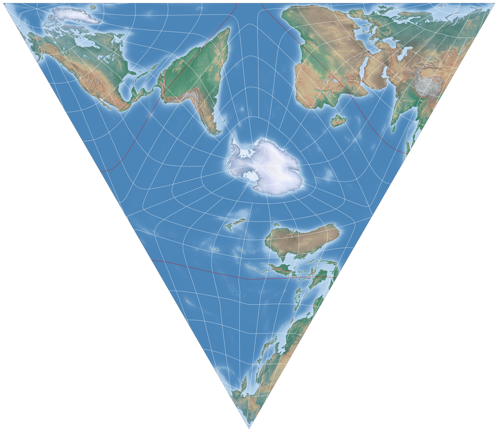
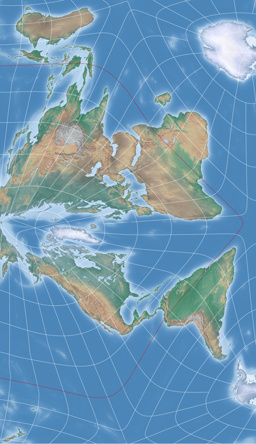
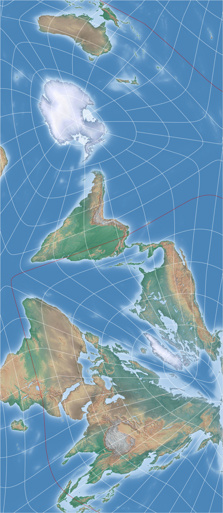
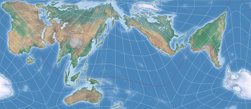
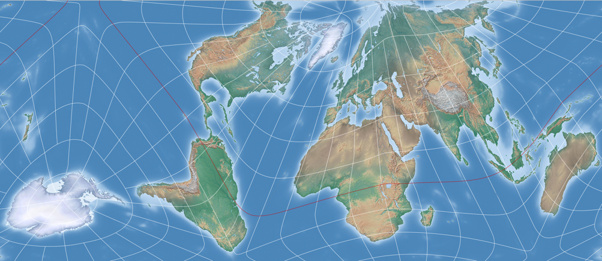
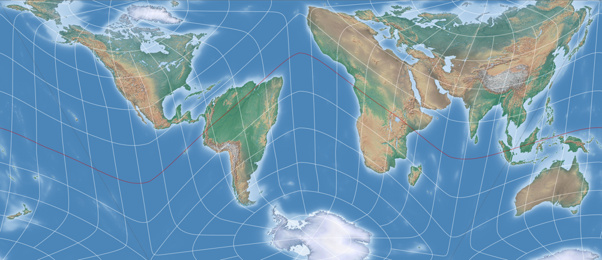
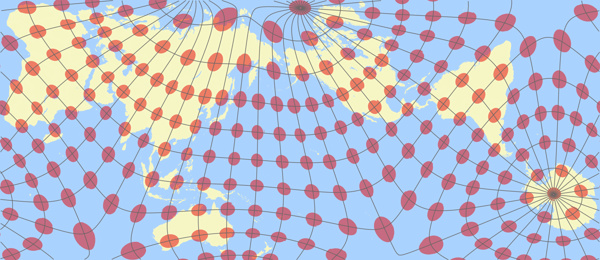
Momentan möchte ich nur darauf hinweisen, dass sie gemäß meiner vorläufigen Analyse zumindest teilweise näher an der echten Flächentreue ist als das Original. Ich werde das genauer untersuchen müssen. Um Euch aber nicht allzu sehr auf die Folter zu spannen, folgen hier schon einmal zwei Darstellungen von Kunimunes AuthaGraph-Variante:

Fußnoten/Quellenangaben

↑ Zwei deutsche Artikel über die AuthaGraph-Karte:
https://www.wired.de/collectio…
https://www.berliner-zeitung.d…
… noch ein deutscher Artikel (samt Video), welcher hervorragend zeigt, wie ein falsches Verständnis der AuthaGraph-Karte alte Missverständnisse durch neue ersetzt, anstatt die Welt besser zu erklären. Es ist erstaunlich, wieviel Unsinn in einen derart kurzen Artikel gepackt wurde:
https://www.welt.de/wissenscha…
… einige mehr oder weniger zufällig ausgewählte englische Artikel:
http://geoawesomeness.com/best…
https://www.quora.com/Why-dont…
https://www.thesun.co.uk/news/…
https://www.stuff.co.nz/world/…
http://www.popularmechanics.co…
https://gizmodo.com/this-wacky…
http://blogs.discovermagazine.…
https://www.wired.com/2016/11/…
https://www.japantimes.co.jp/l…
… und ein weiterer englischer, aber ausgewogenerer Artikel:
https://dmswart.com/2016/11/10…
↑ Marcin Ciura:
Reproducing the AuthaGraph World Map
↑ van Leeuwen, Diederik / Strebe, Daniel:
A “Slice-and-Dice” Approach to Area Equivalence in Polyhedral Map Projections
in: Cartography and Geographic Information Science, Vol. 33, No. 4, 2006, pp. 269-286
gegen Bezahlung verfügbar unter: doi.org/10.1559/152304006779500687

Permalink

Kommentare

Ein Kommentar

Verbleibende Zeichen: 2048

Die folgenden vier Felder auf keinen Fall ausfüllen!

christian Schützenhofer

Hallo Deine Erklärungen, sind fantastisch, auch wenn sie am Anfang Kopfschmerzen beinhalten. Man kann deine Ausführungen tagelang studieren und lesen, höchst interessant und aufschlussreich. Vielen dank dafür.
Habe noch eine Frage beziehungsweise Bitte. Wäre es möglich ein hoch auflösendes Bild (gif) so ab 1500 Pixel zu bekommen?? Wenn ja eines wo alle Kontinente kommplett drauf sind, auch wenn sie dann am Bildrand nochmals erscheinen.

Lg Schützenhofer

Mi, 15.1.2020, 13:17 Uhr MEZ