Falsche Tissot-Grafiken

Sa, 18.12.2021 Falsche Tissot-Grafiken

Aktualisiert: Mo, 10.1.2022

Ein kurzes Geständnis

Ich muss Euch etwas sagen, was ich Euch schon lange hätte sagen sollen: Die Grafiken der tissotschen Indikatrix, die ich hier für jede einzelne Projektion, die ich Euch zeige, verwende… sind eigentlich falsche Tissot-Indikatrizen – sozusagen eine Pseudo-Tissot-Indikatrix! 😳

Die Grafiken verwenden keine echten Tissot-Ellipsen, sondern Kleinkreise – genauer gesagt, Entfernungskreise (Kreise gleicher Entfernung von einem gegebenen Punkt) –, um die Verzerrungen der Projektionen zu visualisieren. Die gute Nachricht ist: Das beeinträchtigt nicht den Sinn und Zweck der Grafiken; man kann sie trotzdem verwenden, um die Art und Verteilung der Verzerrungen in jeder denkbaren Projektion zu betrachten und zu analysieren! Es geht nur darum, dass sie dies auf eine etwas andere Weise darstellen; und dass ich die falsche Bezeichnung verwendet habe.

Darüber hinaus ist der Unterschied zwischen Kleinkreisen und Tissot-Ellipsen überaus wichtig, wenn man die Verzerrungswerte einer Projektion berechnen will, wie es z.B. das Airy-Kavraiskiy-Kriterium macht, welches ich in den letzten Monaten wiederholt erwähnt habe. Allerdings sind meine Grafiken nicht für Berechnungen irgendeiner Art gedacht, sondern nur für eine Visualisierung von Verzerrungen. Dafür sind sie gut geeignet.

Und eigentlich ist das schon alles, was ich heute mitteilen wollte.
Aber nun bin ich ja mehr so der geschwätzige Typ, und falls du Interesse hast, lies weiter, um zu erfahren, was der genaue Unterschied zwischen Kleinkreisen und der echten tissotschen Indikatrix ist, und warum ich die letztgenante nicht auf meiner Website verwende.

Eine lange Erklärung

Teil 1: Der Unterschied

Was ist also der Unterschied zwischen Kleinkreisen und Tissot-Ellipsen? In dem Tissot-Artikel, den ich vor einigen Jahren geschrieben habe, habe ich zur Erklärung gesagt:

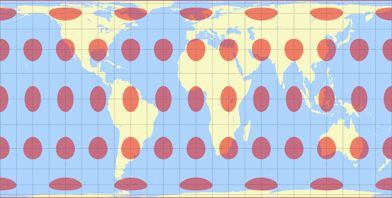
Man stelle sich vor, da kommt jemand mit einem großen Farbeimer daher (einem riesigen Farbeimer!) und malt in regelmäßigen Abständen gleich große Kreise auf die Erdoberfläche. Wenn er fertig ist, sieht die Erde aus dem All betrachtet in etwa so aus wie in der Grafik unten.

Tatsächlich ist dies eine Beschreibung der Kleinkreise, nicht der Tissot-Ellipsen!
Jeder der in der Grafik gezeigten Kreise hat einen Radius von etwa vier Längengrad, was 444 Kilometern entspricht. Es handelt sich also um riesige Kreise, die da jemand auf die Erde gemalt hat. Die Tissot-Ellipsen sind aber infinitesimal, »ins unendlich Kleine gehend«. Nun kann man infinitesimale Ellipsen natürlich nicht sehen, was ihre Sinn, nämlich Verzerrungen zu visualisieren, ein klein wenig torpediert, nicht wahr? Daher werden die Tissot-Ellipsen vergrößert, nachdem sie berechnet worden sind. Man könnte sagen, dass die Ellipsen und die Karte in verschiedenen Maßstäben dargestellt werden.
Kurz zusammengefasst, besteht der Unterschied also darin, dass die echte Tissot-Indikatrix die Verzerrungen an bestimmten, annähernd unendlich kleinen Punkten auf der Karte zeigt, während die Kleinkreise die Verzerrungen eines Gebietes auf der Erde darstellen, nämlich des gesamten Gebietes, welches von dem fraglichen Kreis begrenzt ist.

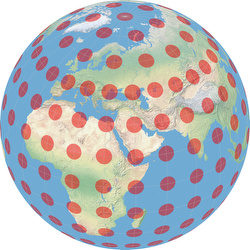
Kommen wir nun zu den sichtbaren Auswirkungen des Unterschiedes. Für viele Projektionen gilt, dass die Differenz extrem gering ist. Betrachte dieses Beispiel mit der Winkel-Tripel-Projektion, in dem die rot gefüllten Punkte die Kleinkreise sind, während die blauen Ellipsen-Umrisse die echte tissotsche Indikatrix darstellen:

Bei dieser Größe denkst Du wahrscheinlich sogar, dass sie absolut identisch sind. Aber betrachte diesen Ausschnitt der nordwestlichen »Ecke« der Karte:

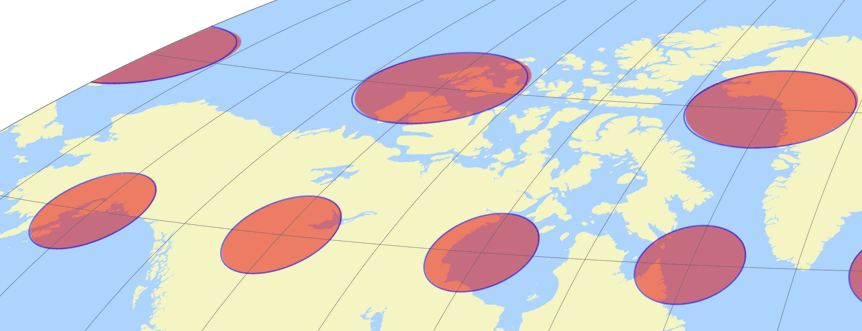
In der oberen Reihe, bei 75°N, kann man nun die Unterschiede erkennen. Und wenn Du genau hinsiehst, kannst Du auch die Unterschiede in der unteren Reihe ausmachen: Am nordöstlichen Rand jeder Ellipse liegt der blaue Umriss tatsächlich innerhalb des roten Punktes, während er sich am südöstlichen Rand außerhalb befindet.

Diese Abweichungen spielen eigentlich keine Rolle – jedenfalls nicht für die Grafiken auf meiner Website. Aber hier folgt ein weiteres Beispiel der Pseudo- und der echten Tissot-Indikatrix in der Hobo-Dyer-Projektion:

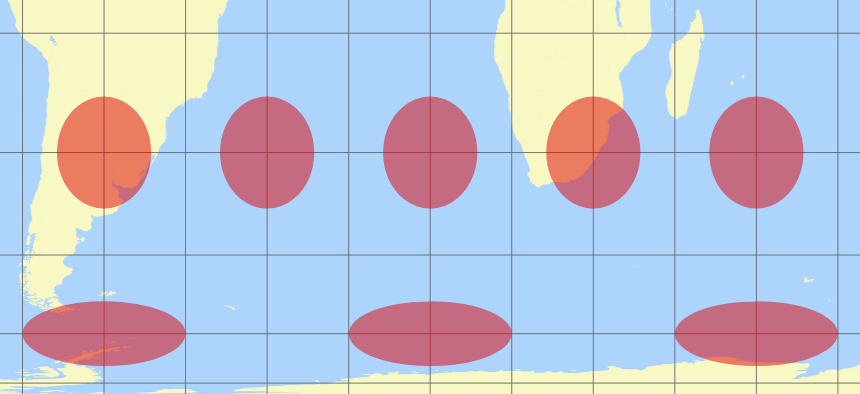
Ich denke, der Unterschied ist ziemlich deutlich – nichtsdestoweniger, hier ist ein Ausschnitt mit den Pseudo-Tissots nahe des Südpols:

Wie Du sehen kannst, sind die roten Punkte eigentlich keine Ellipsen mehr: Der nördliche Rand hat eine andere Krümmung als der südliche, wodurch die Punkte in der oberen Reihe sozusagen »Ei-förmig« werden, und in der unteren Reihe, ääähm… ich weiß nicht, wie man diese Form nennen soll. Die Winkelverzerrungen der Hobo-Dyer-Projektion nehmen rapide zu, während man sich den Polen nähert (da es sich um eine flächentreue Projektion handelt, treten keine Größenverzerrungen auf). Am nördlichen Scheitelpunkt des (deformierten) Kleinkreises im unteren Teil des obigen Bildes beträgt die Winkelverformung 30°, während sie am südlichen Scheitelpunkt etwa 77° erreicht hat. Bei einem solchen Unterschied innerhalb des Kreises ist es kaum verwunderlich, dass er sich zu einer Form krümmt, die keine Ellipse mehr ist. Im Gegensatz dazu lässt sich diese Art der Verformung mit der echten Tissot-Indikatrix nicht beobachten. Auch das ist keine Überraschung – da die echten Tissot-Ellipsen infinitesimal sind, gibt es keine Unterschiede bei den Winkelverformungen innerhalb einer bestimmten Ellipse:

Nun kennst du also den Unterschied zwischen der Pseudo- und der echten Tissot-Indikatrix. Bleibt noch eine Frage…

Teil 2: Warum verwende ich weiterhin die Pseudo-Tissot-Indikatrix?

Als ich die Arbeit an meiner Website vor etwa sechs Jahren angefangen habe, wusste ich nicht einmal, dass die Grafiken, die ich verwende, eine Pseudo-Tissot-Indikatrix zeigen. Aber nun, da ich es weiß (und wie ganz am Anfang gesagt, weiß ich es auch schon eine Weile), warum nutze ich sie dann weiter, anstatt sie durch echte Tissot-Darstellungen zu ersetzen? Ich verwende fünf verschiedene Anwendungen, um die Projektionsgrafiken für meine Website zu generieren: Geocart, G.Projector, Flex Projector, MapDesignerRaster und d3-geo-projection-Skripte.

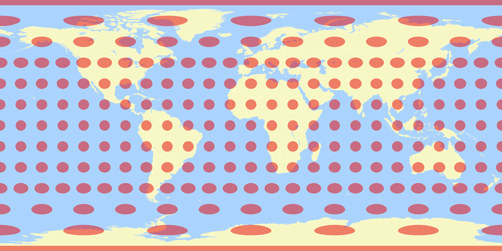
Alle fünf können eine Weltkarte, die in der rechteckigen Plattkarte (auch Plate-Carrée-Projektion genannt) vorliegt, in andere Entwürfe projizieren. Die Eingangskarte, die ich für die Tissot-Darstellug verwende, sieht so aus (das Gradnetz wird später von der jeweiligen Projectionssoftware hinzugefügt):

Wieder ist erkennbar, dass in der Nähe der Pole keine echten Ellipsen gezeigt werden, da es sich eigentlich um Kleinkreise handelt. Ich habe also schon ein falsches Eingangsbild verwendet. Aber es würde auch keinen Unterschied machen, wenn es sich hierbei um die echten Tissot-Ellipsen handeln würde: Ein Bild zu projizieren, wird niemals auf die echte Tissot-Indikatrix hinauslaufen, denn diese muss für jede Projektion extra berechnet werden.

Und warum tue ich das dann nicht?
Weil von den fünf genannten Programmen nur zwei dazu in der Lage sind: Geocart und Flex Projector. Bei Grafiken, die von Geocart erzeugt worden sind, wäre ein bisschen Nachbearbeitung nötig, um sie aussehen zu lassen wie die bisherigen Grafiken (rote Punkte, gelbe Kontinent usw). Für Exporte aus Flex Projector wäre es eine Menge Arbeit.
Und dann hätte ich immer noch keine echte Tissot-Indikatrix bei den Projektionen, die von den anderen drei Programmen gerendert worden sind.

Viel Arbeit, wenig Gewinn.
Denn – sagte ich das schon? – auch mit den Kleinkreisen lassen sich die Verzerrungsverhältnisse visuell gut beurteilen. Und deshalb werde ich sie weiterhin benutzen.

Und eins noch …

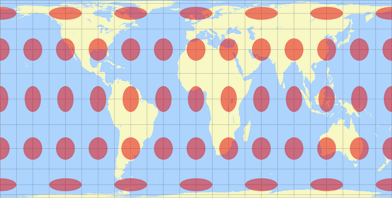
Vor fast vier Jahren habe ich angefangen, neue »Tissot«-Grafiken zu verwenden; allerdings nur für neu hinzugefügte Projektionen. Damals schrieb ich: »die bisherigen Tissot-Grafiken werden also nicht ersetzt«. Nun ratet mal – vor kurzem habe ich angefangen, sie doch noch zu ersetzen. Etwa 90 habe ich schon erledigt, genauso viele habe ich noch vor mir.

Ich werde das nach und nach erledigen (ohne weitere Mitteilung). Bis ich damit durch bin, wird es also noch eine Weile dauern.

Update 10.1.2022:
Zwei Hinweise. Erstens, Peter Denner ist wieder einmal der Retter in der Not! Er hat mir gezeigt, wie mit Hilfe der d3-Skripte mikrometergroße Tissot-Ellipsen gezeichnet werden, die unendlich kleinen Ellipsen so nahe kommen, wie es nur geht. Also könnte ich nun eigentlich auch für die mit d3 erstellen Projektionsgrafiken echte Tissot-Ellipsen zeigen. Aber sorry, das werde ich nicht tun, aus den o.g. Gründen. Zweitens, die alten Pseudo-Tissot-Darstellungen wurden nun endlich vollständig durch die neuen ersetzt. Es sind also immer noch unechte Tissots, aber wenigstens nun in einheitlicher grafischer Darstellung.

Permalink