Fr, 29.7.2022 Lee, Markley, CALM & Grieger
Aktualisiert: Mi, 4.6.2025
Heute habe ich meiner Projektions-Kollektion vier Entwürfe hinzugefügt.
Alle sind winkeltreu mit vergleichsweise geringen Flächenvergrößerungen auf den
Kontinenten, und drei davon zeigen die Erde in einer rechteckigen Karte.
Dies wird ein etwas längerer Blogpost, hier also eine kleine Vorschau,
bevor wir ins Detail gehen:
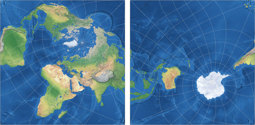
Lee’s winkeltreue tetraedrische Projektion
Zu Beginn möchte ich (mal wieder) John P. Snyder zitieren, aus Flattening the Earth, Seite 266:
The most extensive treatment of the subject of map projections as a mathematical challenge without necessarily a practical outcome was to devise conformal projections for hemispheres or world maps bounded by simple geometric figures (…)
Lee [showed] the world conformally on the faces of all five of the regular Platonic polyhedra (tetrahedron, cube, etc.).
Die umfangreichste Behandlung des Themas der Kartenprojektionen als mathematische Herausforderung, ohne notwendigerweise zu einem praxistauglichen Ergebnis zu kommen, war die Entwicklung winkeltreuer Projektionen für Hemisphären oder Weltkarten, die durch einfache geometrische Figuren begrenzt sind (…)
Lee [zeigte] die Welt winkeltreu auf den Seiten aller fünf platonischen Polyeder (Tetraeder, Würfel usw.).
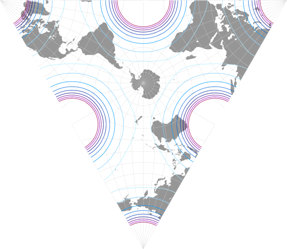
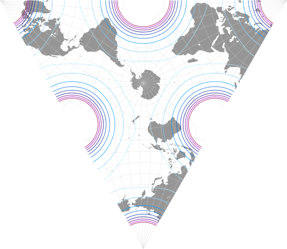
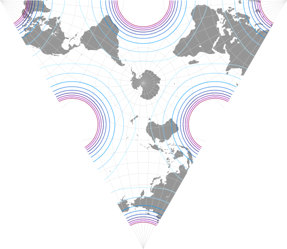
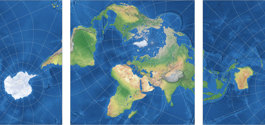
Und hier haben wir eine davon, die tetraedrische Version, 1965 vorgestellt.[1] Für die Grafik in meiner Projektions-Kollektion habe ich mich entschieden, zwei Ansichten zu zeigen, die nord- und die südpolare Lage (wie ich es schon bei anderen tetraedrischen Projektion gemacht habe, nämlich Snyders Tetraeder sowie die van Leeuwen Großkreis- und Kleinkreis-Varianten ). Laut Carlos Furutis hervorragender Website war Lee’s[2] Original auf den Südpol zentriert, leider hat er nicht Zentralmeridian genannt. Er zeige eine Grafik, die einem Zentrum auf 15°W entspricht, während Paul B. Anderson sich für 20°W entschied und Justin Kunimune eine Version mit 22.5°W in die Wikimedia Commons hochgeladen hat.
Welche Variante entspricht dem Original, welche ist die beste? – Ich weiß es nicht. Bei der Grafik für
meine Projektions-Kollektion habe ich mich für Kunimunes Zentrum entschieden. Hier kannst du die
Verteilung der Flächenvergrößerungen in den drei Varianten betrachten;
die Linien stehen für Werte von
1,2; 1,5; 2,0; 2,5; 3,0; 3,5; 4,0; 4,5; und 5,0:
Nebenbei: Der »Zentral«-Meridian ist gewissermaßen Ansichtssache. Zum Beispiel ist die oben gezeigte nordpolare Ansicht auf 150°O zentriert (die gerade Linien, die vom Nordpol zum oberen Scheitelpunkt des Dreiecks verläuft), es könnte aber genau so gut der antipodische Meridian 30°W sein, der zur Mitte der Basis des Dreiecks läuft. Und noch einige andere Längengrade, abhängig von der Ausrichtung des Dreiecks.
Mit einem gut gewählten Projektionszentrum sorgt Lee’s
winkeltreue tetraedrische Projektion also sehr gut dafür, dass die schlimmsten
Flächenvergrößerungen von den Kontinenten ferngehalten werden, aber was
ist mit dem »praxistauglichen Ergebnis«, von dem Snyder gesprochen hat?
Ich glaube kaum, dass irgendjemand eine derartige Weltkarte in einem Atlas
oder einem Bericht nutzen möchte. Ja, sie kann gekachelt werden –
sie den Furuti-Link oben oder
Kunimunes Darstellung –,
und du kannst sie ausdrucken, um einen tetraedrischen Pseudo-Globus zu falten
(Furuti
hat einige schöne Beispiele zum Download bereitgestellt).
Aber beide Anwendungen gehören eher in den Bereich der dekorativen Arbeiten.
Nun, ich nehme an, Lee’s Welt in einem Dreieck ist tatsächlich keine Projektion für praxistaugliche Ergebnisse.
Oder etwa doch?
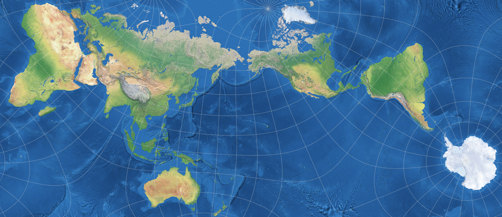
Markleys winkeltreue tetraedrische Karte
Nun, dies ist eine Projektion, die man für praktische Zwecke nutzen kann!
Falls Du anderer Meinung bist: Ich werde am Ende dieses Blogposts kurz auf die
Frage der »praktischen Zwecke« eingehen.
Sie ist winkeltreu, hat vergleichsweise niedrige Flächenvergrößerungen auf den Landflächen,
die Anordnung der Kontinente ist nicht allzu verwirrend, und hey, sie ist sogar rechteckig!
Die Leute lieben rechteckige Weltkarten!
Tja, aber die Sache ist: Dies ist Lee’s
winkeltreue tetraedrische Projektion!
In seiner Abhandlung von 2020[3] berichtet
F. Landis Markley, dass er (in Unkenntnis über Lee’s frühere Entwicklung)
die konforme Projektion auf ein Tetraeder 1982 erneut erfunden hat.
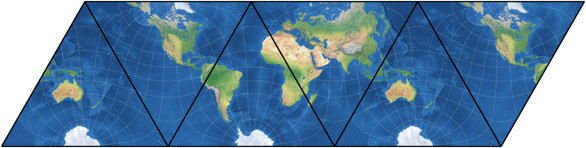
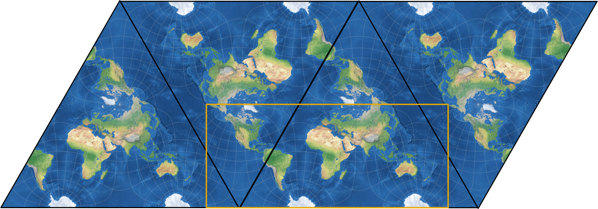
Er verwendete ein spezifisches Projektionszentrum (siehe unten) und arrangierte
die vier Seiten des Tetraeders (zwei davon erscheinen zweimal) folgendermaßen:
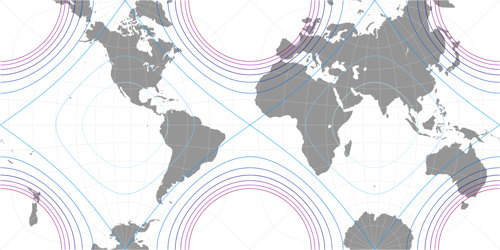
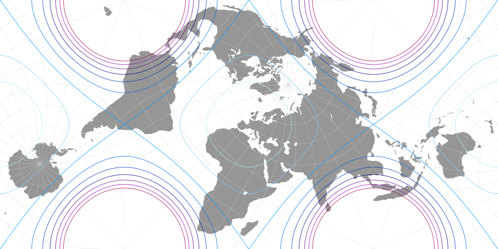
Anschließend muss man nur noch die nicht benötigten Teile am linken und rechten Rand abschneiden und man gelangt zur rechteckigen Karte. Markley entwickelte seine Konfiguration als Verbesserung der Guyou-Projektion, also ist es sinnvoll, die Verteilung der Flächenvergrößerungen bei diesen beiden zu vergleichen:
Beide sind nicht allzu verwirrend, d.h. dass die Anordnung der Landmassen
noch sehr vertraut wirkt, wenn man Weltkarte in der äquatorständigen Ansicht gewohnt ist,
welche auf oder nahe des Nullmeridians zentriert sind; obgleich die Kontinente
ein wenig zu »herum zu tänzeln« scheinen.
Überdies zeigen beide Projektionen die Pole jeweils zweimal.
Daher würde lautet meine persönliche Empfehlung, sie nur für Karten zu verwenden, bei denen das Gradnetz gezeigt wird.
Guyous Projektion gefällt mir immer noch sehr gut, aber in Bezug auf die
Verteilung der Vergrößerungen auf den kontinentalen Arealen kann ich
zustimmen, dass Markleys Arrangement eine Verbesserung darstellt.
Beide Projektion lassen sich kacheln, so dass man
auf einfache Weise mit eigenen Varianten aufwarten kann: Wenn dir z.B. das unterbrochene
Antarktika nicht gefällt, füge eine Erweiterung hinzu, um es komplett zu zeigen
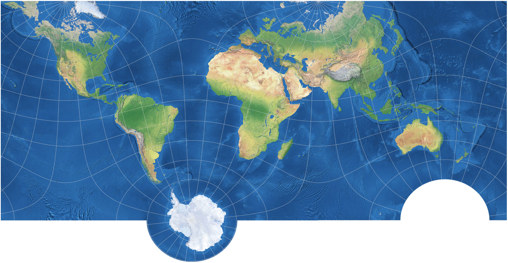
(in meiner Darstellung, am Beispiel von Markleys Karte, ohne Wiederholungen); oder erzeuge eine Pazifik-zentrierte
Version – hier ebenfalls mit einer Erweiterung, diesmal um Sibirien ununterbrochen
zu zeigen und mit Wiederholungen:
Kommen wir noch einmal auf das Projektionszentrum zurück:
Wie oben gesagt, hängt das davon ab, wie die verwendete Software mit Lee’s Projektion umgeht.
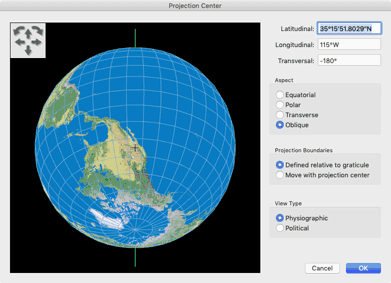
In Geocart
muss das Zentrum wie folgt festgelegt werden:
Latitidinal: 35°15′51.8029′N (oder 35.26438969)
Longitudinal: 115°W
Transversal: 180°
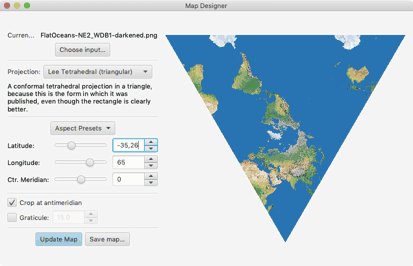
In Justin Kunimunes Kartenprojektions-Paket
lautet die Konfiguration hingegen:
Latitude: -35,26
Longitude: 65
Ctr. Meridian: 0
Die exakten Koordinaten für Geocart wurden von der u.g. d3-Implementation abgeleitet. Beachte, dass Kunimunes Software genau die antipodischen Werte verwendet – abgesehen davon, dass hier nur zwei Nachkommastellen erlaubt sind. Der Unterschied zu dem Längengrad in Geocart beträgt auf der Erdkugel aber nur rund 488 Meter, was bei einer Weltkarte natürlich zu vernachlässigen ist.
Da Kunimunes Programm nicht die einzelnen Seiten des Tetraeders, sondern eine komplette Weltkarte generiert, stellt sich das Arrangieren und Ausschneiden aus dem Zwischenergebnis etwas anders dar:
Und zu guter Letzt möchte ich auch noch auf die Implementation von Markleys Karte für d3-geo-projection hinweisen. Ohne diese Präsentation wäre mir Markleys Arbeit gar nicht bekannt, also herzlichen Dank!
Meiner Meinung nach ergibt Markleys Arrangement eine wunderbare winkeltreue Weltkarte. Und es beweist, dass Lee’s tetraedrische Projektion zu einem praxistauglichen Ergebnis führen kann.
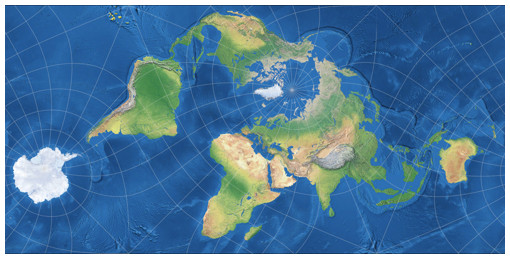
Habe ich gerade im Singular gesprochen?CALM – Conformal Authagraph-Like Map
In seinem 2019er blogpost “Tetrahedral projections” hat Farhan Adrian eine weitere Konfiguration von Lees Projektion vorgestellt, die ein Arrangement wie die Authagraph-Karte zeigt. Die Authagraph wurde vor ein paar Jahren ziemlich gehypt, obgleich dies zumindest teilweise wohl an einigen Missverständnissen und falschen Behauptungen lag (was ich mal kurz angesprochen habe). Wie auch immer, die Anordnung der Kontinente ist interessant, also ist es schön, eine winkeltreue Variante zu sehen.
In einer persönlichen E-Mail-Konversation hat mir Herr Adrian mitgeteilt, welches Projektionszentrum er benutzt hat
– vielen Dank, Farhan! 🙏 – und einen Namen für den Entwurf vorgeschlagen:
CALM für Conformal Authagraph-Like Map projection
(winkeltreue Authagraph-ähnliche Kartenprojektion).
Also, die CALM-Projektion wurde ursprünglich mit Kunimunes Software unter Verwendung folgender Konfiguration entwickelt:
Latitude: 77
Longitude: 143
Ctr. Meridian: -163
… was folgenden Werten in Geocart entspricht:
Latitidinal: 77°S
Longitudinal: 37°W
Transversal: 17°
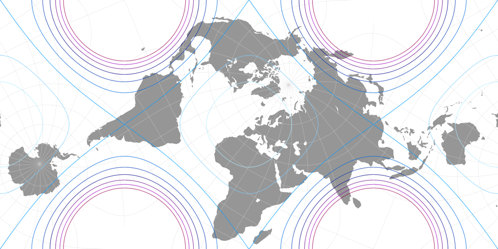
Die Konstruktion der CALM-Projektion ist identisch zu der oben gezeigten Vorgehensweise, also müssen wir das nicht noch einmal durchkauen. Betrachten wir aber die Flächenvergrößerungen im Vergleich zu Markleys Projektion:
Wie immer, wenn man das Projektionszentrum ändert (oder eine Rotation des Koordinatensystems durchführt, wie man auch sagen kann), gibt es gewisse Regionen, die davon profitieren, während andere benachteiligt werden. Insgesamt bevorzuge ich abermals Markleys Arrangement. Aber die CALM-Projektion ist wirklich nicht schlecht; obgleich die Vergrößerung von Brasiliens östlichster Spitze und Australiens Westküste schon etwas störend ist und das Aufblasen der Neusibirischen Inseln fast schon schmerzt[4]. Darüber hinaus wird der »Tanz der Kontinente« für meinen Geschmack hier doch ein bisschen zu wild. Als Vorteil können wir aber verbuchen, dass alle alle größeren Landmassen inkl. Antarktika ohne Unterbrechungen gezeigt werden.
Aber das Beste an der CALM-Projektion ist: Sie gefällt mir besser als die originale Authagraph-Karte und ihr »mutierter Nachkomme«, Kunimunes IMAGO. Und das kommt von mir, der ich üblicherweise sage: »Oh, mir gefällt diese Projektion, aber sie würde sich auch gut machen mit ein bisschen weniger Flächenvergrößerung« – was mehr oder weniger der Grund war, warum ich Projektionen wie Wagner BCW-A I, F13 Copycat und Guyou-Wagner vorgelegt habe. In diesem Falle aber sind die Nachteile der »beinahe, aber nicht ganz flächentreuen Darstellung« der Authagraph und ihrem Nachkommen, welche sich in deutlich sichtbar verzerrten Formen niederschlagen, doch zu prominent.
Aber glaubt mir das nicht einfach – seht und entscheidet selbst:
Vergleiche CALM- und IMAGO-Projektion!
Hinweis: Im Interesse einer besseren Vergleichbarkeit habe ich eine Atlantik-zentrierte Version in meine Projektions-Kollektion aufgenommen, aber natürlich kann man auch eine Pazifik-zentrierte Variante erzeugen (also so, wie der Authagraph-Karte überlicherweise gezeigt wird):
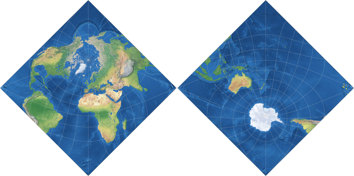
Griegers triptychiale Projektion
Und hier noch eine Neuanordnung einer klassischen winkeltreuen Projektion: 2019 präsentierte Björn Grieger[5] eine interessante schiefachsige Version des Peirce Quincuncx von 1879. Ein älterer schiefachsiger Aspekt von Peirces Projektion ist bekannt als Adams Hemisphären in einem Quadrat, und da der letztgenante die Welt so darstellt, wie ich es benötigte (nämlich in zwei separaten Hemisphären), verwendet ich diesen, um die triptychiale Karte zu erzeugen. Unter Verwendung von Geocart stellt sich die Konstruktion der Projektion wie folgt dar:
- Erzeuge zwei Karten mit Adams’ hemisphärischer Projektion. Setze das Projektionszentrum der einen auf 45°N, 0°O und der anderen auf 45°S, 180°O.
- Rotiere die fertige Karte der »nördlichen« Hemisphäre (d.h. die, die den Nordpol enthält) um 45° im Uhrzeigersinn, und die »südliche« um 45° gegen den Uhrzeigersinn.
- Exportiere die zwei Karten, z.B. als TIFF-Datei, und öffne sie in einem Grafikprogramm.
- Schneide die »südliche« Hemisphäre vertikal in zwei Hälften. Platziere die Hälfte, die den Südpol enthält, links der »nördlichen« Hemisphäre, die andere nach rechts. Füge die drei Teil-Karten nahtlos zusammen.
Die Anordnung der drei Kartenteile entspricht der eines Triptychons, daher der Name triptychiale Projektion. (Um ehrlich zu sein, bin ich nicht sicher, ob das Adjektiv »triptychial« überhaupt existiert, aber – wen kümmert’s? Jetzt existiert es!)
Das »Layout« der Kontinente erinnert an den Canters W23 – das überrascht nicht, denn das Ziel beider Entwürfe war es, alle größeren Landmassen ohne Unterbrechungen zu zeigen, und es gibt nicht viele Projektionszentren, die darauf hinauslaufen. Für Laien könnte diese Darstellungsweise ein wenig verwirrend sein. Das ist an sich nicht unbedingt etwas Schlechtes; es kann nie schaden, die Leute zum Denken anzuregen. Aber man sollte schon vorsichtig abwägen, für welche Art von Karten eine derartige Projektion geeignet ist.
Kommen wir zu den Verzerrungen! Abermals finden sich sichtbare Vergrößerungen – die entsprechende Grafik wird weiter unten gezeigt – in Afrika (wie bei Markley) und Südamerika (wie in CALM), aber diesmal sind andere Teile betroffen: Das südliche Afrika und die Westküste von Südamerika. Die malaiische Halbinsel und Sumatra sind noch stärker betroffen – aber die Galapagos-Inseln schießen den Vogel ab! Sie werden etwa vierzigfach vergrößert, in etwa so viel, wie die Neusibirischen Inseln bei der CALM-Projektion.
Ich wollte überprüfen, ob man nicht mit einer besseren Verteilung der Verzerrungen auf den
Kontinentalflächen aufwarten kann, also verlegte ich den zentralen Meridian von 0°
nach 10°W für die nördliche und 170°O für die südliche Hemisphäre.
Und tatsächlich wurde Africa ein bisschen besser, Südamerika wurde deutlich besser,
die malaiische Halbinsel & Sumatra wurden viel besser,
und die Galapagos-Inseln wurden verdammt viel besser.
Das bedeutet, dass sie näher an ihre tatsächliche Größe heran geschrumpft wurden.
Ob das nun wirklich »besser« ist, ist natürlich Ansichtssache…
Natürlich, wie oben schon gesagt, muss irgendjemand auch der Leidtragende sein, und in diesem Fall wären das Ostsibirien, Japan und (vermutlich am Auffälligsten) der indische Subkontinent. Trotzdem gefiel mir meine Konfiguration besser, also nahm ich Kontakt zu Björn Grieger auf und fragte, warum er sich für die von ihm vorgestellte Anordnung entschieden hat. Hier ist seine Antwort, zitiert mit freundlicher Genehmigung:
Ich hatte auch mit Variationen der Projektionsparameter experimentiert, um die exorbitante Vergrößerung der Galapagos-Inseln zu vermeiden. Es gibt ja einen kontinuierlichen Bereich im Parameterraum, der zu akzeptablen Projektionen führt, jede mit Vorteilen in manchen Gebieten und Nachteilen in anderen. Letztendlich habe ich mich einfach für die ganz glatten Zahlen entschieden, beide Rotationen um exakt 45°. Die Vergrößerung der Galapos-Inseln lenkt die Aufmerksamkeit auf sie, und das habe ich ihnen dann einfach zugestanden, man könnte sagen, wegen ihrer Bedeutung für die Entwicklung der Evolutionstheorie. Die »glatten« Winkel führen auch dazu, dass die Knoten eines 15°-Koordinatennetzwerks genau an den kritischen Punkten liegen, was hilft zu verstehen, was dort passiert.
Und es gibt, wie später merkte, noch einen Grund, der gegen mein Projektionszentrum spricht. Er wird dir wahrscheinlich auffallen, wenn wir uns jetzt endlich die Visualisierung der Verzerrungen ansehen, und zwar von Griegers Original-Zentrum und meinem Versuch:
Mein Projektionszentrum durchtrennt Neuseeland. Autsch!
Man könnte das Zentrum nun wieder leicht verschieben, um das zu vermeiden, aber damit rutschen
natürlich jene Gebiete, die ich verbessern wollte, zurück in die etwas ungünstigeren Bereiche.
Oder man verwendet eine Erweiterung, wie ich sie oben bei Markleys winkeltreuer tetraedrischer Karte gezeigt habe;
aber das wäre eine sehr kleine Erweiterung und ich bin der Meinung, dass diese immer ein wenig
plump aussehen.
Eine weitere Möglichkeit ist es, die südliche Hemisphäre nicht in zwei gleich große Hälften
zu zerschneiden, sondern einen Teil ein wenig größer zu machen, so dass Neuseeland
ohne Unterbrechungen bleibt. Hier ein Beispiel, diesmal mit einem 10°-Gradnetz:
Natürlich vermasselt das Griegers schönes symmetrisches Triptychon.
Zugegeben, die Asymmetrie ist kaum sichtbar, stellt in meinem Augen nichtsdestoweniger
ein kleines Ärgernis dar.
In meiner Version werden also bestimmte Bereiche verkleinert (sie nähern sich also ihrer tatsächlichen
Größe an), was natürlich dazu führt, dass andere vergrößert werden – und
die Symmetrie der Komposition wird aufgegeben.
Unterm Strich: Ich glaube nicht, dass meine Variante eine tatsächlich Verbesserung ist
– sie ist nur eine Alternative, die du wählen kannst, falls sie deinen Vorstellungen
besser entspricht. Was eigentlich immer der Fall ist, wenn man eine Rotation des Koordinatensystems
durchführt, also weiß ich nicht, warum ich es überhaupt (schon wieder) erwähne. 😉
Update 4.6.2025: Eine größere Version (1988 × 994 Pixel) dieser Karte kann nun
betrachtet und runtergeladen werden.
So viel zu den neuen Projektionen. Wie oben versprochen, möchte ich nun noch einmal auf eine bestimmte Frage zurückkommen…
»Praxistaugliche Ergebnisse«?
Kann man bei diesen Karten von »praxistauglichen Ergebnissen« sprechen? Die The Geocart Projection List führt die Guyou-Projektion als geeignet für »novelty maps«[6] auf, was nahelegt, dass eine einigermaßen ähnliche Karte wie Markleys eher in den Bereich der dekorativen Anwendungen fällt. Und ja, auch ich würde sie nicht unbedingt zur Verwendung in einem Atlas oder einen Bericht empfehlen (es sei denn, der Inhalt des Berichts würde nach einer winkeltreuen Karte verlangen, aber mir fällt keine Art von Bericht ein, bei der das der Fall wäre). Andererseits – stelle Dir eine allgemein-geografische Weltkarte vor, die du an deine Wand hängen willst, mit vielen Beschriftungen für Länder, Städte und physische Merkmale. Ihr Hauptzweck wäre also, Informationen zu vermitteln, aber es kann sicher nicht schaden, wenn sie darüber hinaus auch noch attraktiv aussieht, oder?
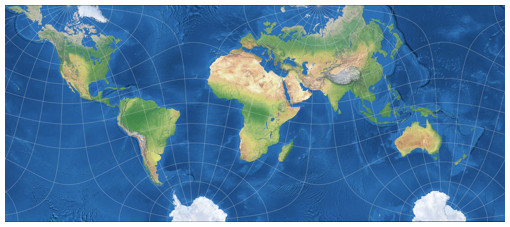
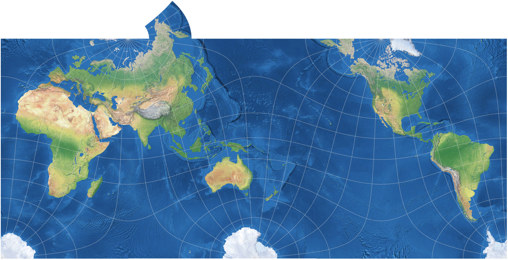
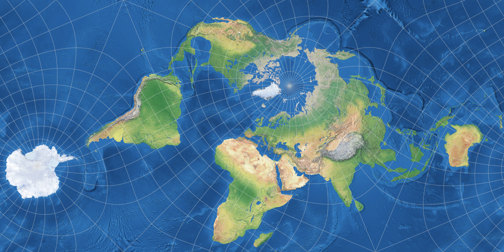
Um mir selbst einen Eindruck davon zu verschaffen, habe ich eine Weltkarte (in der Rektangularprojektion mit Schnittparallelen auf 35° N/S), die ich vor einigen Jahren angefertigt habe, umprojiziert in Markleys winkeltreuer tetraedrische Karte. Die Beschriftungen wurden dabei mit einbezogen, daher werden sie gebeugt und gebogen und zusammengedrückt und auseinander gezogen:
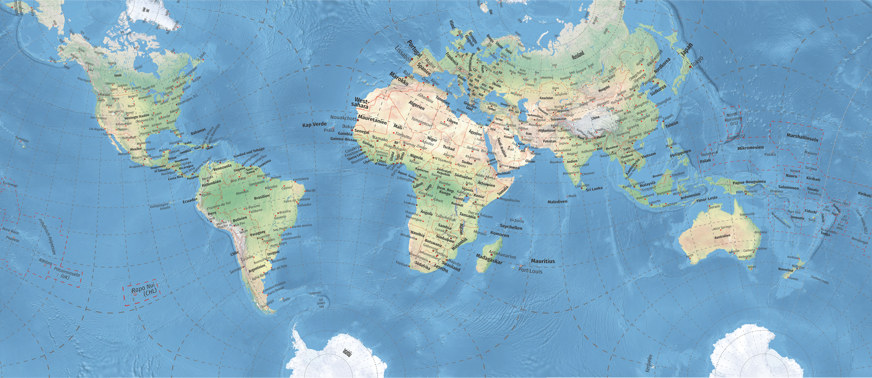
Umprojizierte Weltkarte, Markleys winkeltreue tetraedrische Projektion.
Öffne eine sehr große Version
(2765 × 1200) in einem neuen Browserfenster/-tab.
Nun, für mich geht das! Das heißt, es würde gehen, wenn es denn vernünftig gemacht würde. Zwar gefällt mir sogar, dass die Grundlinie der Beschriftungen entlang der Breitenkreise verläuft, die Verkleinerungen und Vergrößerungen der Schriften gefallen mir jedoch nicht. Wie auch immer, ich denke man kann eine Karte dieser Art als »praxistaugliches Ergebnis« bezeichnen.
Dies trifft eventuell in geringerem Maß für die CALM und besonders Griegers Projektion zu. Letztere kann ich mir dafür gut vorstellen für solche thematischen Karten, für die derzeit gerne mal die Dymaxion-Karte verwendet wird, die z.B. die Ausbreitung des Menschen zeigen. Die Eigenschaft der Winkeltreue ist sicherlich nicht notwendig für derartige Karten, stellt aber aufgrund der geringen Flächenvergrößerungen auch kein Problem dar. Und Lee’s originale Konfiguration – nun, ich habe testweise mal eine Klimakarte erzeugt. Und irgendwie gefällt mir die Verteilung der Klimazonen, wie es vom Zentrum zum Äquator wärmer wird und dann zu den Ecken des Dreiecks hin wieder kälter. Zugegebenermaßen finde ich das unübersichtlicher als die üblichen (meist zylindrischen oder pseudozylindrischen) Klimakarten, so dass der Haupt-Einsatzzwecke von Lee’s Variante tatsächlich im dekorativen Bereich verbleiben dürfte.
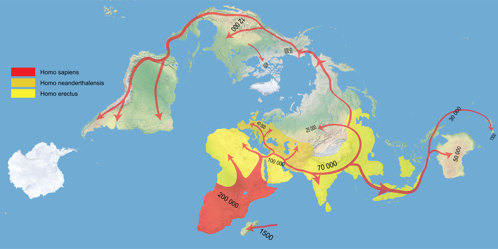
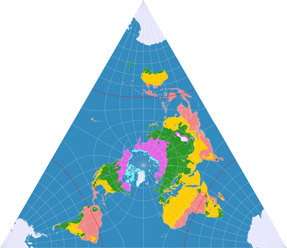
Auch hier habe ich die Beschriftungen mitprojiziert.
Auf einer echten Karte sollten die Beschriftungen natürlich nicht kopfüber stehen…
Aber ungeachtet der Frage, ob die hier vorgestellte Werke nun praxistauglich sind oder nicht: Es sind alle sehr schöne winkeltreue Weltkarten, welche die Vergrößerungen auf den Kontinenten gering halten. Und daher willkommene Neuzugänge!
Quellenangaben / Fußnoten
-
↑
L.P. Lee, 1965:
Some Conformal Projections Based on Elliptic Functions
doi.org/10.2307/212415 (bezahlter Zugang) -
↑
Apostrophen-Alarm! Ich weiß, dass der Genetiv von Lee im Deutschen Lees geschrieben wird
und nicht Lee’s – und bei den anderen Namen mache ich es ja auch richtig.
Bei diesem Namen aber fand ich einfach, dass es mit Apostroph besser aussieht, also habe ich
mal eine Ausnahme gemacht und die Regeln der Zeichensetzung bewusst missachtet.
Ha! Ich bin ein Revoluzzer! 😉 -
↑
F. Landis Markley, 2020:
Tetrahedral Map Projection - ↑ Aber die gigantischen Neusibirischen Inseln hatten auch ihr Gutes: Ich habe festgestellt, dass (nicht nur) sie auf dem Kartenbild, welches ich seit 2015 nutze, um die grünen und roten Silhouette-Karten zu erzeugen, fehlen! Ooops. Offensichtlich habe ich es damals mit der Generalisierung etwas übertrieben…
-
↑
Die Projektion wurde bereits 2010 entwickelt. Der Öffentlichkeit präsentiert in
B. Grieger, 2020: Optimized global map projections for specific applications: the triptychial projection and the Spilhaus projection, EGU General Assembly 2020, Online, 4–8 May 2020, EGU2020-9885, doi.org/10.5194/egusphere-egu2020-9885.
Auf jeden Fall den »Display File«-Button am Ende der Seite anklicken! - ↑ novelty im englischen Wiktionary: Meant primarily for display rather than functional use – Hauptsächlich zum dekorativen, nicht praktischem Einsatz gedacht.







 Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Kommentare
Sei der erste, der einen Kommentar hinterlässt!