Fr, 15.1.2021 Mehr Umbeziffern für d3-geo-projections
Hinweis: In der englischen Version dieser Seite spreche ich vom customizable Wagner.
Im Deutschen habe ihn meistens den anpassbaren Wagner genannt – aber ich fand auch schon immer,
dass das ein wenig holprig klingt. Aber was sollte ich sonst schreiben? »Individualisierbar«?
»Parametrisierbar«? Maßgeschneidert ist eher das Ergebnis des, ääähm, »maßschneiderbaren« Entwurfs…
Das gefiel mir alles nicht, also hab ich mich entschieden, ihn den flexiblen Wagner zu nennen.
Ist auch nicht viel besser, aber in meinen Augen und Ohren noch die angenehmste Variante.
Vielleicht fällt mir ja irgendwann noch etwas richtig Gutes ein…
Im Juni 2018 habe ich den anpassbaren Wagner VII in einer Implementation für
d3-geo-projections vorgestellt. Heute lege ich nach und
stelle anpassbare Varianten von Wagner I/II und einigen Projektionen mit gleichabständigen Breitenkreisen
(entlang des Zentralmeridians) vor, inkl. zwei unterschiedlichen Herangehensweisen für den Wagner III.
Das wäre mir nicht möglich gewesen ohne jede Menge Hilfe von Peter Denner.
Thanks a lot, Peter! 🙏
Es gibt allerdings ein paar Unterschiede zur Implementation des Wagner VII.
Dieser Blogpost befasst sich hauptsächlich mit dem Warum: Warum gibt es Unterschiede?
Warum gibt es (scheinbar) redundante Parameter?
Wenn Du daran weniger interessiert bist, sondern eher am Wie – Wie kann ich die Projektionen
an meine eigenen Wünsche anpassen? –, dann lies nur die folgende Kurzfassung und gehe dann zu
Flexible Wagner-Projektionen mit d3-geo – Seven Of Nine.
Beachte, dass ich hier neue Funktionen für d3-geo-projections vorschlage! Sie gehören nicht zur aktuellen Distribution, sie sind noch nicht vollständig getestet, sie mögen Fehler enthalten und könnten noch geändert werden!
Kurzfassung
Zum besseren Verständnis blicken wir noch einmal kurz zurück:
Die vorhandene Implementation des flexiblen Wagner VII/VIII erlaubt die Anpassung von vier Parametern: Die Länge der Pollinie,
die Krümmung der Breitenkreise, das Ausmaß der Flächenvergrößerung und das Längenverhältnis der Hauptachsen (Äquator zu Zentralmeridian).
Der entsprechende Quellcode sieht z.B. so aus:
d3.geoWagner()
.poleline(65)
.parallels(84)
.inflation(25)
.ratio(200)
Dabei akzeptiert
poleline() Werte von 0 (= Pollinie ist genauso lang wie der Äquator) bis 90 (= punktförmiger Pol);
parallels() Werte von 0 (= Breitenkreise sind gerade Linien) bis 180 (= starke Krümmung);
inflation() von 0 (= keine Flächenvergrößerung, also flächentreu) bis 99,999;
und ratio() beschreibt das Verhältnis der Achsen, nämlich die prozentuale Länge des Äquators im
Vergleich zum Zentralmeridian. Eigentlich ist hier jede Zahl größer als 0 und kleiner als 1000 erlaubt, aber der Bereich
sinnvoller Werte ist natürlich viel geringer.
Kommen wir nun zu den neu vorgeschlagenen Funktionen. Wie Du sehen wirst, gibt es da Gemeinsamkeiten und Unterschiede.
🌐
Beispiel des vorgeschlagenen flexiblen Wagner I/II:
d3.geoWagner2()
.poleline(0.5)
.inflation(20)
.ratio(200)
Bezüglich inflation() und ratio(): Siehe oben.
poleline() hingegen wird hier als Wert zwischen 0 (punktförmiger Pol) und 1 (Länge d. Pollinie = Länge d. Äquators) notiert.
Die Gründe dafür werden unten genannt.
🌐
Der vorgeschlagene flexible Wagner III:
d3.geoWagner3()
.poleline(0.5)
.ratio(200)
.phi0(40)
Dabei funktionieren poleline() und ratio() wie beim Wagner I/II –
zusätzlich können wir die Schnittparallele phi0() bestimmen, die eigentlich ebenfalls
das Seitenverhältnis beeinflusst. Gründe dafür: Siehe unten.
🌐
Und letztendlich der flexible Wagner ESP, der Projektionen mit gleichabständigen Breitenkreisen (engl.
Equally Spaced Parallels) erzeugt:
d3.geoWagnerEquallySpacedParallels()
.parentProjection(9)
.poleline(70)
.parallels(50)
.ratio(200)
.xfactor(100)
Alle Wagner-Projektionen sind jeweils von einer Mutter-Projektion abgeleitet. Während diese bei den anderen
hier vorgestellten Varianten feststeht, kann sie bei Wagner ESP aus mehreren Möglichkeiten ausgewählt werden.
Dafür ist der Parameter .parentProjection() zuständig.
.poleline().parallels().ratio()
– diese werden entsprechend dem o.g. Wagner VII/VIII notiert.
Und dann haben wir noch .xfactor(), der wie .ratio() das Seitenverhältnis der Karte ändert.
Den Grund dafür, Du ahnst es, wird unten erklärt.
🌐
Uuuund dann gibt’s noch den Apian II. Keine Parameter, schlicht und einfach
d3.geoApian2().
🌐
So weit die Kurzfassung. Wenn das genug Informationen für Dich sind – wie oben gesagt,
kannst Du nun Beispiele betrachten und ausprobieren.
Für nähere Informationen – weiterlesen!
Umbeziffern – was war das nochmal?
Ich habe an verschiedenen Stellen über das Umbeziffern geschrieben, zuletzt im o.g. Blogpost vom Juni 2018.
Fassen wir das aber noch einmal zusammen: Nimm einen Ausschnitt aus einer »Mutter-Projektion«,
der durch einen begrenzenden Breitenkreis und einen begrenzenden
Meridian definiert wird, projiziere die gesamte Erde auf diesen Ausschnitt, bringe ihn auf den Maßstab der originalen Projektion
und strecke ihn horizontal. Der Breitenkreis bestimmt die Länge der Pollinie,
der Meridian bestimmt die Krümmung der Breitenkreise in der neuen Projektion.
Wagner hat aber auch die Möglichkeit einer kontrollierten Flächenvergrößerung hinzugefügt.
Zum Beispiel ist der begrenzende Breitenkreis im
Wagner-Böhm I
auf 65° Nord/Süd gesetzt,
der begrenzende Meridian auf 84° Ost/West, die Flächenvergrößerung auf 25% (bei 60° N/S, ein Referenzbreitengrad,
der im Skript hartcodiert ist) und das Längenverhältnis der Achsen beträgt 200% (= der Äquator ist doppelt so lang
wie der Zentralmeridian).
Die Notation dieser Projektion sieht in den d3-Skripten dann so aus:
d3.geoWagner().poleline(65).parallels(84).inflation(25).ratio(200)
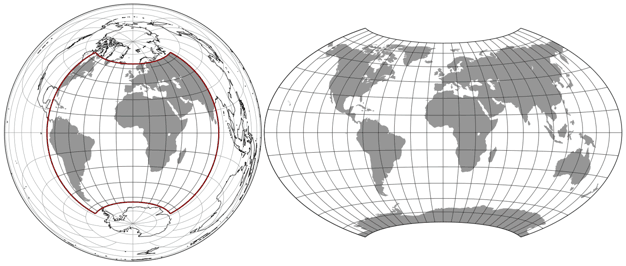
Lamberts flächentreue Azimutalprojektion mit den markiertem Grenzbreitenkreis und -meridian (links) und der resultierende Wagner-Böhm I
Im Falle des Wagner VII war die Mutter die äquatorständige flächentreue Azimutalprojektion von Lambert. Aber alle neun Projektionen, die nach Wagner benannt wurden, wurden durch den Einsatz des Umbezifferns entwickelt … wobei Wagner manchmal eine etwas andere Herangehensweise benutzt hat.
Sehen wir und das im einzelnen an.
Der flexible Wagner I/II
Genau wie Wagner VII und VIII lassen sich der Wagner I und II aus derselben Formel generieren, der einzige Unterschied besteht in der Flächenvergrößerung: Beim Wagner I ist sie auf Null gesetzt und erzeugt somit eine flächentreue Karte. Beim originalen Entwurf II entschied sich Wagner für eine Vergrößerung von 20% (auf 60° Nord/Süd wie oben genannt). Die Notation in meiner Implementation sieht folgendermaßen aus:
d3.geoWagner2().poleline(0.5).inflation(20).ratio(200)
Zunächst fällt der fehlende Parameter .parallels() auf:
Wagner I und II sind von der
Sinusoidal-Projektion
abgeleitet – einem pseudozylindrischen Entwurf mit den für diese
Gruppe typischen geraden Breitenkreisen. Diese Eigenschaft wird beibehalten, folglich gibt es keinen Parameter,
der die Krümmung der Breitenkreise festlegt.
Aber was ist mit .poleline(0.5)? Hier wird doch nicht etwa 0,5° Nord/Süd als begrenzender Breitengrad festgelegt?
Nein, natürlich nicht. Bei den Entwürfen, die heute als Wagner I bis VI bekannt sind, ging der Urheber anders vor:
Er definierte die Länge der Pollinie relativ zur Länge des Äquators. Er begann die Entwicklung der finalen Formel mit
der Variablen c = 0,5, welche eine Pollinie generiert, die halb so lang wie der Äquator ist.
Beachte, dass dies wirklich nur eine andere Ausdrucksweise ist, die Länge der Pollinie festzulegen
– Wagner vergaß auch nicht anzumerken, dass der
Wert von 0,5 einem Grenz-Breitenkreis von 66,42° entspricht. In den Formeln, die von den Eingangsparametern zur fertigen
Projektionsformel führen, arbeitete er aber mit dem o.g. Wert von c.[1]
Wenn ich also weiß, dass c einer bestimmten begrenzenden Breite entspricht, warum verwende ich dann nicht diese,
um die Notation konsistent zu halten?
Das Problem ist: Ich bin mies in Mathe.
Ich kann eine Formel transkribieren, zum Beispiel von C-Syntax nach JavaScript, was ich im Falle
der finalen Formel getan habe – im Falle des Wagner I/II war meine Vorlage Evendens C-Implementation
des Wagner I.[2] Die Umrechnung der Eingabe-Parameter in die Werte, welche der finalen Formel übergeben werden, habe
ich die Schritte umgesetzt, die Wagner selbst aufgezeigt hat.
Was ich nicht kann, ist es, Formeln umzuschreiben. Ich habe einfach nicht die mathematischen
Kenntnisse, um sagen zu können: »Oh, ich ersetze mal diese Variable c durch ein
vernünftiges ψ1 für die Grenzbreite…«
Es blieb mir also gar nichts anderes übrig, als die relative Länge der Pollinie beizubehalten.
Ich muss zugeben, dass mich das ein bisschen ärgert. Andererseits: Wenn sowohl Äquator, als auch
Pollinie als gerade Linien ausgeführt sind, ist es vielleicht sogar intuitiver, anstelle des eher abstrakten Grenzbreitenkreises
das Längenverhältnis dieser beiden Linien zu benutzen.
Jetzt fragst Du vielleicht: »Aber warum benutzt Du dann nicht wenigstens einen prozentuellen Wert, wie
Du es auch schon beim Längenverhältnis von Äquator zu Zentralmeridian machst?« – Gute Frage,
spielen wir das mal durch:
Dem .ratio() entsprechend, könnte man auch .poleline(200) schreiben, um festzulegen,
dass der der Äquator doppelt so lang wie die Pollinie ist. Aber was dann ist mit einem punktförmigen Pol?
In diesem Fall beträgt die Länge der Pollinie genau Null, und
200% oder 1,000% oder 78,435% von 0 sind immer noch 0. Das funktioniert also nicht.
Und andersrum, wenn man .poleline(50) schreibt, um festzulegen, dass die Pollinie halb so lang
ist wie der Äquator? Das ist natürlich genau das gleiche wie 0.5, es würde also funktionieren,
und wenigstens hätte man dann wieder einen prozentuellen Wert anstelle eines Multiplikators.
Ja – aber beim Wagner VII/VIII ergibt .poleline(80) eine sehr kurze Pollinie, während der gleiche Code
beim Wagner I/II für eine sehr lange Pollinie sorgen würde. Erhöht man diesen Wert, nähert sich die
Pollinie beim VII/VIII einem punktförmigen Pol an, während sie sich beim I/II der Länge des Äquators annähern
würde.
Ich fand das zu verwirrend.
Mit einem Wert für .poleline(), der beim Wagner I/II zwischen 0 und 1 liegt, sieht man
wenigstens auf den ersten Blick, dass da irgendetwas anders sein muss als beim Wagner VII/VIII.
Zugegeben: Es ist ein bisschen ärgerlich, dass sich die Notation unterscheidet.
Aber ich denke, unterm Strich ist dies die beste Lösung.
(Vielleicht wäre es eine gute Idee, diesem Parameter einen anderen Namen zu verpassen, aber mir
ist nichts eingefallen, was weniger verwirrend wäre. Ich bin offen für Vorschläge.)
Wenn Du die möglichen Resultate des flexiblen Wagner I/II sehen willst, hüpfe rüber zur interaktiven Demo. (Sorry, die gibt es derzeit nur in Englisch.)
Der flexible Wagner III
Die Mutter-Projektion des Wagner III ist der
Apian II,
eine pseudozylindrische Projektion mit gleichabständigen Breitenkreisen. Also können wir abermals auf
den Parameter .parallels() verzichten, da es keine Krümmung gibt
– aber auch das Ändern der Flächenvergrößerung via
.inflation() fällt weg: Diese Änderung würde zwangsläufig dazu führen, dass die Breitenkreise
nicht mehr im gleichen Abstand zueinander stehen.
Bisher bleiben also nur die Parameter .poleline().ratio() übrig – wobei ersterer
wie beim Wagner I/II als Wert zwischen 0 und 1 notiert wird.
Damit es nicht zu einfach wird 😉, fügen wir einen neuen, verwirrenden Parameter hinzu:
.phi0().
phi0 ist in den d3-Skripten der übliche Weg, φ0 zu schreiben, und das ist die
sog. Schnittparallele, die jenen Breitengrad kennzeichnet, der als maßstabsgerecht angesehen wird.
Als Effekt bewirkt die Änderung von .phi0(), dass sich die Seitenverhältnisse der Projektion
ändern.
Hä? Wie bitte? Aber dafür ist doch der .ratio() zuständig, oder?
Ja, eigentlich schon. Das muss ich ausführlicher erklären:
Wagner hat beide Methoden vorgesehen. Er verwendete die Variable p = 0,5,
um das Längenverhältnis der Achsen zu beschreiben, entwickelte damit die finale Formel
und fügte am Ende die Möglichkeit hinzu, eine Schnittparallele zu setzen. Ich habe das immer
als Alternative angesehen: Wenn man das Längenverhältnis ändern will, kann man entweder
p ändern oder es bei 0,5 belassen und stattdessen
eine Schnittparallele setzen. Und kürzlich bin ich über eine Abhandlung gestolpert, in der
beide Parameter geändert wurden.
Damit meine ich natürlich die Abhandlung von Nedjeljko Frančula, über die ich kürzlich schon berichtet habe. Ich möchte hier nur kurz wiederholen, dass Frančula die Verzerrungswerte verschiedener Projektion (darunter der Wagner III) optimiert hat. Dabei hat er beide Möglichkeiten zur Änderung der Seitenverhältnisse genutzt, weil dies in diesem Zusammenhang sinnvoll ist.
Nun ja, sieh Dir die interaktive Demo an!
Dort kannst Du z.B. sehen, dass
d3.geoWagner3().poleline(0.5).ratio(147).phi0(0)
und
d3.geoWagner3().poleline(0.5).ratio(200).phi0(40)
identisch sind (aber beachte den unterschiedlichen Scale [Maßstab] im Abschnitt »Customize Map«). Oder rufe
d3.geoWagner3().poleline(0.69).ratio(195).phi0(44)
auf, um eine von Frančulas optimierten Varianten zu sehen.
Der flexible Wagner ESP – Umbeziffern mit gleichabständigen Breitenkreisen
Vor drei Jahren habe ich den WVG-9 präsentiert, ein quick&dirty-hack des flexiblen Wagner IX.
Ich wollte immer mal eine aufgeräumte Version erstellen, hab es aber nie gemacht. Bis Mr. Peter Denner
mich kürzlich darauf hingewiesen hat, dass es da einen Fehler gab. Ich habe versucht, ihn zu beseitigen, bin
aber gescheitert. Also ist Peter eingesprungen und hat nicht nur den Fehler behoben, sondern mir auch noch
aufgezeigt, wie man die Funktion sehr einfach dafür verwenden kann, das Umbeziffern auf andere Projektionen
mit gleichabständigen Breitenkreisen, die schon Bestandteil der d3-geo-projections-Distribution sind,
anzuwenden. (Daher die Bezeichnung ESP = equally spaced parallels = gleichabständige Breitenkreise.)
Während die Funktion also auf meinen Original-Code für den WVG-9 basiert, stammt der Großteil der Arbeit von Peter.
Zunächst einmal haben wir also nun einen neuen Parameter, der die »Mutter-Projektion« festlegt:
.parentProjection()
Unglücklicherweise muss auch hier eine Zahl übergeben werden – schöner wäre es, den Namen der
Mutter-Projektion zu verwenden, aber das geht leider nicht.[3] Hier ist also die
aktuelle Liste der möglichen Mutter-Projektionen, der existierenden Wagner-Projektionen, die von
ihnen abgeleitet sind,
und der Zahlen, die Du übergeben musst, um sie zu nutzen.
Wie Du sehen kannst, taucht dort noch einmal der Wagner III auf, den wir oben schon abgekaspert haben
– darauf komme ich später noch einmal zurück.
| Mutter-Projektion | Variante von | Aufrufen mit |
|---|---|---|
| Sinusoidal | Wagner III | .parentProjection(3) |
| Apian II | Wagner VI | .parentProjection(6) |
| mittabstandstr. Azimutal | Wagner IX | .parentProjection(9) |
| van der Grinten IV | — | .parentProjection(10) |
| American Polyconic | — | .parentProjection(11) |
| Nicolosi »telophasisch« | — | .parentProjection(12) |
| Rectangular Polyconic | — | .parentProjection(13) |
Für die drei Wagner-Projektionen habe ich einfach die römische Ziffer in die entsprechende
arabische »übersetzt«, und bei den anderen habe ich dann einfach bei 10 weitergezählt…
Ich bin von dieser Herangehensweise wirklich nicht begeistert, hatte aber keine Idee,
wie ich das besser lösen kann.
.poleline() und .parallels() verwenden, wie beim eingangs gezeigten Wagner VII,
wieder die Grenz-Breitenkreise und -Meridiane der Mutter-Projektion. .ratio() funktioniert
wie bei allen Beispielen. Aber abermals füge ich einen weiteren Parameter an, der zunächst redundant
erscheint:
.xfactor() – was soll das nun wieder?
.xfactor() (den ich so genannt habe, weil mir nichts anderes einfiel) reduziert oder
erhöht die Breite der Karte. Der notierte Wert ist eine prozentuale Angabe der Breite, welche
sich aus .ratio() ergibt. Die Gründe für die Verwendung dieses Parameters entsprechen
denen, die wir oben schon hatten: Wagner hat es so gemacht. Und aus guten Grund, jedenfalls aus damaliger Sicht:
Er entwickelte die Formel mit der Variablen p = 2 (entspricht .ratio(200) im unserer Implementation),
kam bei der finalen Formel an und sagte am Ende, dass man die Verteilung von Verzerrungen verbessern kann, indem
man »die x noch mit einem Faktor a < 1 [versieht]«, und führte ein Beispiel mit a = 0,88 auf,
was auf eine Projektion ähnlich des Winkel Tripel Bartholomew hinausläuft.[4]
Das war deshalb sinnvoll, weil es damals keine elektronischen Rechenhelfer gab.
Wenn Du also eine Tabelle mit den kartesischen Koordinaten hast – und Wagner hat diese in
seinem Buch zur Verfügung gestellt –, musst Du einfach nur alle x-Werte mit dem Faktor
versehen, den Du wünschst, und fertig.
Das ist viel weniger Arbeit, als die komplette Tabelle mit einem anderen Wert von p erneut durchzurechnen.
Aber heutzutage haben wir elektronische Rechenhelfer, und angesichts der Tatsache, dass
.poleline(70).parallels(50).ratio(200).xfactor(88) die gleiche Karte rendert wie
.poleline(70).parallels(50).ratio(176).xfactor(100) (auch hier: abgesehen vom nominellen Maßstab)
hatte ich mich eigentlich schon entschlossen, .xfactor() fallen zu lassen und die Bestimmung
der Breite allein mit .ratio() zu bestimmen.
Aber – vielleicht ahnst Du es schon – Frančula verwendet mal wieder beide Parameter, und
im Bestreben, seine Varianten inklusive ihrer berechneten Verzerrungswerte so genau wie möglich reproduzieren zu
können, musste ich den Parameter beibehalten.
Abermals lade ich Dich herzlich ein, das (englische)
interaktive Beispiel
zu besuchen:
Dort kannst Du sehr schön sehen, dass die Änderung von .ratio() eine Karte horizontal streckt und
gleichzeitig vertikal staucht (oder umgekehrt) – es handelt sich um eine flächenbewahrende Änderung
(eine sog. affine Abbildung), das Ausmaß der Flächenvergrößerung ändert sich also nicht.
Bei .xfactor() hingegen dehnt oder staucht sich die Karte nur in horizontaler Richtung,
was auf eine Änderung der nominellen Flächenverhältnisse hinausläuft.
Beachte, dass es nicht erforderlich ist, beide Werte zu benutzen: Es ist möglich, nur einen zu notieren,
beim jeweils anderen wird dann die Default-Einstellung übernehmen.
Außer der interaktiven Demo kannst Du auch den WVG-9 benutzen, der mittlerweile
WVG-ESP heißt.
Im interaktiven Beispiel kannst Du ein paar Schieberegler hin- und herziehen und
die Projektion »on-the-fly« geändert, während der WVG-ESP jedesmal die Seite neu lädt, wenn Du
andere Parameter setzt. Andererseits erlaubt der WVG-ESP bis zu drei Nachkommastellen bei jedem Wert,
während das interaktive Beispiel auf halbzahlige Werte beschränkt ist. Darüber hinaus
bietet der WVG-ESP noch ein paar weitere Optionen.
… und nebenbei: Apian II
Wie oben gesagt, greift der Wagner ESP auf die Formeln von Mutter-Projektionen zurück,
die schon Bestandteil von d3-geo-projection waren. Der Wagner VI war bisher nicht enthalten,
also hat Peter die entsprechende Formel geschrieben.
Apian II hat selbst keine Parameter, man ruft ihn also einfach auf mit: d3.geoApian2().
Resümee
Ich habe drei Varianten von flexiblen Projektionen für die Verwendung mit d3-geo-projections vorgeschlagen
(zusätzlich zu einer bereits exitierenden),
die Wagners Transformationsmethode des Umbezifferns nutzen.
Manche haben von den anderen Varianten abweichende Parameter, aber das liegt in der Natur der Sache.
Ärgerlicher ist, dass die Notation der Parameter in einigen Fällen abweicht, obwohl sie eigentlich
die gleiche Auswirkung haben. Das könnte wahrscheinlich behoben werden – von jemandem, der mehr von der
Mathematik versteht als ich.
Manche Parameter sind redundant, man könnte sie weglassen, sofern man nicht gerade auf minimale Verzerrungen
nach einer bestimmten Metrik aus ist. Andererseits können sowohl die unterschiedlichen Notationen,
als auch die Redundanzen hilfreich sein, bestimmte existierende Projektionen genau nach Spezifikation
des Urhebers zu rendern.
Meiner Meinung nach ist der flexible Wagner I/II nicht besonders interessant, denn sinusoidale Meridiane scheinen nicht sehr beliebt zu sein, und es gibt ohnehin schon jede Menge pseudozylindrischer Projektionen… Bestenfalls könnte die Möglichkeit, das Ausmaß der Flächenvergrößerung frei bestimmen zu können, einen gewissen Nutzen erweisen.
Der flexible Wagner III ist hilfreich, wenn man eine Projektion mit gleichabständigen Breitenkreisen braucht, die der mathematischen Beschreibung nach Frančula folgt. Er ist aber gewissermaßen überflüssig, da er (mit einer anderen Beschreibung) im Wagner ESP enthalten ist.
Der Wagner ESP hingegen ist sehr interessant, hauptsächlich dank von Peter Denner, der mit gezeigt hat, wie man die Transformationsmethode auf andere Projektionen ausweiten kann. Das gefällt mir wirklich sehr gut!
Das einzige, was mir noch besser gefallen würde, wäre es, die Transformation des Wagner VII/VIII auf andere Projektionen anzuwenden, denn dort hat man die Möglichkeit, die Flächenvergrößerung frei zu bestimmen… Das sollte theoretisch möglich sein, aber leider werde ich das nicht hinbekommen.
Beispiele von möglichen Projektionen, die von den vorgeschlagen Funktionen gerendert werden,
sowie den Quellcode zur Integration in d3-geo-projections, gibt es unter
Flexible Wagner-Projektionen mit d3-geo – Seven Of Nine.
Nachtrag
Ich hatte diesen Blogpost schon fast fertiggeschrieben, als Peter Denner mir noch etwas geschickt hat:
Eine Funktion, um Canters’ Optimierung des Wagner IX zu erstellen. Ich habe sie dem
Quelltext hinzugefügt, weil das für manche Leute (z.B. mich) sicher interessant ist; aber wahrscheinlich
ist es nicht nötig, sie in d3-geo-projection aufzunehmen: Canters’ Projektion kann natürlich
mit dem Wager ESP berechnet werden, wenn man die korrekten Werte kennt.
Da Canters aber mathematisch eine etwas Herangehensweise gewählt hat, habe ich es nie geschafft,
sie zu finden; also habe ich im WVG-9 immer nur Annäherungen gezeigt.
Mit Peters Funktion war ich nun in der Lage, die richtigen Werte zu bestimmen. 😁
Hier sind sie:
d3.geoWagnerEquallySpacedParallels()
.parentProjection(9)
.poleline(67.131)
.parallels(86.562)
.ratio(206.7978)
.xfactor(80.7486)
Hier verwende ich bis zu vier Nachkommastellen, um so nah wie möglich an das Original heranzukommen.
Beachte: Wenn Du Canters Optimierung im interaktiven Beispiel
aufrufst, bekommst Du weiterhin eine Annäherungen, da dieses Beispiel auf die Verwendung von halbzahligen Werten beschränkt ist.
Der WVG-ESP hingegen
verwendet die o.g. Nachkommastellen. Ich denke, somit kommt man nah genug dran, um von der echten
Projektion zu sprechen, nicht nur einer »Approximation«.
Fußnoten
- ↑ Wagner, Karlheinz: Kartographische Netzentwürfe. Leipzig 1949/Mannheim 1962, S. 180 – 181
- ↑ Gerald I. Evenden, libproj4, cartographic projection library.
- ↑ Nedjeljko Frančula: Die vorteilhaftesten Abbildungen in der Atlaskartographie. Bonn 1971. Online verfügbar auf researchgate.net
-
↑
In den d3-Skripten gibt es eine Funktion namens
mutate(), mit der man gewisse Parameter einer Projektion ändern kann. Da sie hauptsächlich für Schnittparallelen u.ä. gedacht ist, akzeptiert sie nur numerische Werte. Möglicherweise lässt sich das Ganze auch anders realisieren, aber momentan weiß ich nicht, wie… - ↑ Wagner 1949/1962: S. 214 – 217

 Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Kommentare
Sei der erste, der einen Kommentar hinterlässt!