Neues bei den Wagner-Variationen

Fr, 8.6.2018 Neues bei den Wagner-Variationen

Aktualisiert: Fr, 6.3.2020

Bei diesem Update dreht sich alles um die Projektions-Variationen, die sich durch Wagners Transformationsmethode des Umbezifferns erzeugen lassen. Solltest Du nicht wissen, wovon ich Rede: Darüber habe ich mich in dem Artikel Das Umbeziffern ausführlich ausgelassen.

Ich beginne mit einem Hinweis, der mit meiner Site eigentlich gar nichts zu tun hat…

Geocart 3.2

Die professionelle Kartenprojektions-Software Geocart liegt seit kurzem in der Version 3.2 vor. Diesen Update enthält – neben vielen anderen neuen Projektionen – auch den generalized Wagner, mit dem sich unter der Verwendung von Wagners Methode maßgeschneiderte Karten erstellen lassen.

Dies erscheint mir erstens erwähnenswert, weil ich hier auf kartenprojektionen.de so viel über die Wagner-Variationen geschrieben habe. Zweitens, und finde ich noch wichtiger: Als Wagner 1941 den Kartennetzentwurf vorgestellt hat, den wir heute Wagner VII nennen – hat er im Grunde genommen gar keinen Kartennetzentwurf vorgestellt. Er hat ein Verfahren vorgestellt, mit dem sich aus einer Mutter-Projektion etliche andere Projektionen erzeugen lassen.
Nun wird dieses Verfahren – 77 Jahre nach seiner Vorstellung und 33 Jahren nach Wagners Tod – meines Wissens erstmals konsequent in einer Software umgesetzt. Endlich bekommen wir die Wagner-Projektionen in einer Form, wie Wagner sie beabsichtigt hatte!

Und ja, natürlich habe ich auch an anderer Stelle, z.B. im Blogpost über die Sinucyli-Projektion schon von »der kommenden Geocart-Version« gesprochen… nun ist sie verfügbar!

Neues beim WVG-7

Im Wagner-Variationen-Generator (WVG-7 und WVG-9) habe ich eine kleine Neuheit eingeführt:
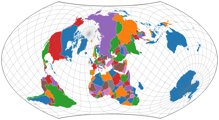
Man kann nun auch das Projektionszentrum sowie die Achsenneigung festlegen. Dies ermöglicht Ergebnisse wie z.B. diese hier:

Eine Implementation für d3

Im WVG benutze ich die Skripte von d3js.org, um die Projektionen zu rendern.
Aber als ich ihn vor etwas mehr als einem Jahr fertiggestellt habe, habe ich einen quick&dirty-Ansatz gewählt: Die benötigten Werte wurden per PHP errechnet und in das JavaScript eingesetzt.
Igitt!

Nun habe ich mich endlich an eine sauberere Lösung herangewagt, bei der alle Berechnungen in JavaScript durchgeführt werden (wie üblich bei den d3-Skripten). Aber:
Auch diese Lösung ist vorläufig, eher ein »proof of concept«. Ich habe bisher nicht überprüft, ob sie den d3-Code-Konventionen entspricht! Seit November 2018 ist meine Implementation Bestandteil von d3-geo-projections – nun, nachdem Philippe Rivière meinen Quellcode aufgeräumt und verbessert hat. Besten Dank, Philippe! :-)

Aber bevor ich auf die eigentliche Implementation zu sprechen komme, möchte ich noch einmal kurz auf Wagners Methode des Umbezifferns eingehen, so dass Du die verwendeten Parameter nachvollziehen kannst, ohne die ausführlicheren Beschreibungen zu lesen.

Wagners 1941 vorgestellte Idee besteht darin, eine vorhandene »Mutter-Projektion« zu nehmen – nämlich, im Falle von Wagner VII/VIII, den flächentreuen querachsigen Azimutalentwurf.
Dann …

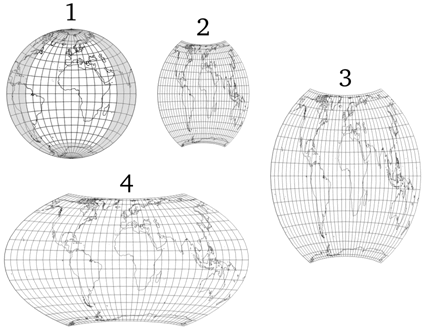
wird ein Teil der Mutter-Projektion bestimmt, definiert durch einen oberen und unteren Breitenkreis sowie einen linken und einen rechten Meridian (65° N/S; 60°O/W beim Wagner VII);
die gesamte Erdoberfläche wird auf diesen Ausschnitt projiziert;
die neue Karte wird auf den ursprünglichen Maßstab der Mutterprojektion zurückgebracht;
und horizontal unter Beibehaltung der Flächentreue bis zum gewünschten Längenverhältnis der Achsen gestreckt.

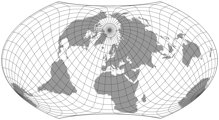
Die folgende Illustration visualisiert diese vier Schritte für die Projektion, die wir heute Wagner VII (oder Hammer-Wagner) nennen:

1949 hat Wagner diese Grundidee erweitert, indem er die Möglichkeit einer vorgeschriebenen Flächenverzerrung hinzugefügt hat, und zwar durch Angabe der gewünschten Größe der Flächenverzerrung. Als Beispiel führte er eine Flächenvergrößerung von 1,2 bei 60° Nord/Süd an, welches in der als Wagner VIII bekannten Projektion resultiert:

Nun kann man also durch die Wahl der begrenzenden Breitenkreise und Meridiane, das Längenverhältnis der Achsen und – sofern man keine flächentreue Projektion benötigt – das Ausmaß der Flächenvergrößerung eine Reihe von Karten ganz nach eigenen Wünschen erzeugen.
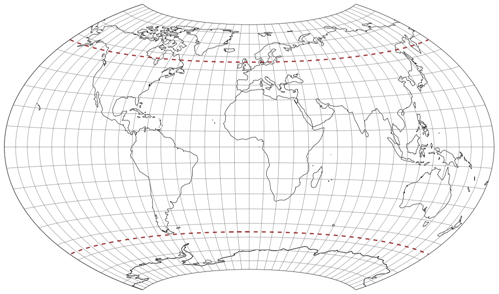
Zum Beispiel hat Dr. Rolf Böhm 2006 eine Variante vorgestellt, in welcher er die begrenzenden Breitenkreise auf 65° und die begrenzenden Meridiane auf 84° gelegt, die Flächenvergrößerung bei 60° auf 1,25 erhöht hat, während die Achsen weiterhin im Verhältnis 1:2 stehen. Das Ergebnis zeigt im Vergleich zum Wagner VIII somit eine kürzere Pollinie, stärker gekrümmte Parallelkreise und eine leicht erhöhte Flächenvergrößerung zu den Polen hin.
(Auf meiner Website habe ich diese Variante Wagner-Böhm I getauft.)

Darüber hinaus hat Dr. Böhm eine Notation vorgeschlagen, mit der sich jede mögliche Wagner-Variation eindeutig identifizieren lässt (und jetzt kriechen wir langsam auf meine d3-Implementation zu), indem er die oben hervorgehobenen Werte hintereinander geschrieben hat. Für das Ausmaß der Flächenvergrößerung sowie das Längenverhältnis der Achsen entschied er sich für prozentuale Werte, so dass seine o.g. Variante folgendermaßen geschrieben wird: 65-84-60-25-200.

Diese Parameter werden von Wagner selbst und Böhm als
ψ₁, λ̅₁, φ₁, S₁ und p bezeichnet (in der vorgenannten Reihenfolge).

ψ₁ ist der begrenzende Breitenkreis und bestimmt die Länge der Pollinie: 90 steht für einen punktförmigen Pol, gegen Null nähert sich die Pollinie der Breite des Äquators an;
λ̅₁ bestimmt als begrenzender Meridian die Krümmung der Breitenkreise: Bei Null werden sie als gerade Linien (wie bei einem Pseudozylinder) ausgeführt; der Maximalwert mit der stärksten Krümmung liegt bei 180;
φ₁ ist der Referenz-Breitenkreis für das folgende Ausmaß der Flächenvergrößerung;
S₁ bestimmt das Ausmaß der Flächenvergrößerung beim Parallelkreis φ₁. Wie gesagt, hat sich Dr. Böhm hier für einen prozentualen Wert entschieden, ein Wert von 25 steht also für eine Flächenvergrößerung mit dem Faktor 1,25. Der Mindestwert ist 0 (= flächentreue Projektion), der Maximalwert ist < 100 (in meiner Implementation: 99,999).
p schließlich bestimmt das Längenverhältnis der Hauptachsen und wird abermals prozentual notiert: Der Wert von 200 erzeugt einen Äquator, der doppelt so lang ist wie der Zentralmeridian.
p muss größer 0 sein, einen Maximalwert gibt technisch gesehen nicht. Halbweg sinnvolle Werte liegen aber irgendwo zwischen 50 und 500.

Falls es mir nicht gelungen ist, die Parameter verständlich zu erklären… warte noch ein wenig, es kommt noch etwas, was alle Unklarheiten beseitigen sollte!

In der d3-Implementation werden vier dieser fünf Werte verwendet.
Nur vier? Was ist mit dem fünften?
Ich habe mich entschlossen, den Parameter φ₁ wegzulassen, denn man kann jede gewünschte Flächenvergrößerung auch als Wert für 60° N/S schreiben: Eine Vergrößerung von 1,6 (oder 60 in der Böhm-Notation) auf 70° entspricht 1,32 (oder 32) auf 60°.
Aus Gründen der Einfachheit habe ich mich entschieden, die Angabe der Vergrößerung im Skript immer auf 60° N/S zu beziehen.
Eigentlich war es Faulheit, denn dieser Weg macht die Validierung der Eingabewerte viel einfacher…

Und nun komme ich auch endlich zum eigentlichen Punkt: Unter Verwendung meiner Implementation kannst Du jede mögliche Variation des Wagner VII (ob flächentreu oder nicht) auf einfache Weise erzeugen. Hier folgt der Codeschnippsel für den oben gezeigten Wagner-Böhm I – auf Fils Anregung hin wurden die Variablennamen geändert, damit sie etwas beschreibender sind:

d3.geoWagner()
  .poleline(65)
  .parallels(84)
  .inflation(25)
  .ratio(200)

Während Wagner tatsächlich mit diesen Eingangs-Parametern gearbeitet hat, sehen die Werte in der endgültigen Projektions-Formel anders aus. Diese Werte habe ich im bereits erwähnten Artikel C_x, C_y, m₁, m₂ und n genannt (nach der Implementation von Gerald I. Evenden in libproj4, 2005, libproj4.maptools.org/).
(Du wirst auch gleich noch sehen, warum ich das erwähne.)

Kommen wir nun also endlich zur eigentlich d3-Implementation des Customizable Wagner:

Ich habe Beispiele mit dem kompletten Sourcecode bereitgestellt.
Siehe https://kartenprojektionen.de/d3-customizable-wagner/.
Die statischen Beispiele 1 - 4 zeigen den Sourcecode, der für die d3-Skripte benötigt wird, im interaktiven Beispiel kannst Du die Möglichkeiten von Wagners Methode erforschen, indem Du ein paar Schieberegler hin- und herschiebst. Wenn es noch unklar ist, wie sich die Eingabeparameter auf die fertige Projektion auswirken – dieses Beispiel sollte beim Verständnis helfen! Dieses Beispiel zeigt auch die Werte, welche für die Übergabe an die endgültige Formel errechnet werden, und ändert sie on-the-fly.

Sorry, die Beispiele sind derzeit nur in englischer Sprache verfügbar. Ich nehme aber an, dass Du ein wenig Englisch beherrscht, sofern Du Dich schon mit den d3-Skripten beschäftigt hast, denn schließlich liegt deren gesamte Dokumentation auch nur in Englisch vor…

Viel Spaß!

Permalink