Neue Projektionen

Di, 28.8.2018 Neue Projektionen

Aktualisiert: Mo, 10.9.2018

Heute habe ich der Liste auf meiner Website ein paar neue Projektionen hinzugefügt. Einige sind Varianten von Entwürfen, die schon zuvor gelistet wurden, andere sind komplett neu.

Unterbrochene Varianten von McBryde / McBryde-Thomas

Die Projektionen von McBryde und McBryde-Thomas habe ich schon eine ganze Weile gelistet – von einigen aber fehlte noch die jeweilige unterbrochene Variante, die ich hiermit nachreiche: McBryde P3, McBryde Q3, McBryde-Thomas Flat-Pole Parabolic und McBryde-Thomas Flat-Pole Sinusoidal.

Update 10.9.2018: Arrggghh! Beim Update der Datenbank habe ich nicht aufgepasst, und daher wurden die vier oben gezeigten Projektion auf der Website nicht aufgelistet. Das ist nun behoben.

Zwei weitere Projektionen von Frank Canters

2002 hat Frank Canters eine Reihe von low-error-Projektionen vorgestellt.^[1] Seine Methode bestand darin, Streckenverzerrungen zu optimieren; basierend auf der Theorie, dass sich die Reduktion von Streckenverzerrungen auch vorteilhaft auf Winkel- und Größenverzerrungen auswirkt.
Aus dieser Reihe sind 10 Entwürfe schon seit längerer Zeit auf meiner Website vorhanden, bei allen bis auf einen handelt es sich dabei um vermittelnde Projektionen.

Allerdings hat Canters auch flächentreue Varianten vorgelegt, von denen ich nun zwei hinzugefügt habe. Ihre kompletten Bezeichnung lautet:
Low-error equal-area transformation of the sinusoidal projection with twofold symmetry, equally divided, straight parallels and a correct ratio of the axes
… und der eine Entwurf trägt den Zusatz not including Antarctica in the optimisation und der andere (wie Du vielleicht schon vermutest) including Antarctica in the optimisation.

Übersetzung: Flächentreue low-error Transformation der Sinusoidal-Projektion mit doppelter Symmetrie, gleichabständig geteilten geraden Breitenkreisen und einen korrekten Verhältnis der Achsen;
mit und ohne Berücksichtung von Antarktika in der Optimierung.
low-error heißt »mit geringer Fehlerquote«, m.W. wird aber auch in der deutschen Kartographie der englische Begriff benutzt.

Aus naheliegenden Gründen bevorzuge ich die Notation, die Dr. Böhm vorgeschlagen hat, und nenne sie Canters W33 und Canters W34.

Als Abkömmlinge der der Sinusoidal-Projektion handelt es sich bei beiden um Projektionen mit punktförmigen Pol (d.h. die Meridiane laufen an den Polen zusammen), allerdings sehen beide (besonders W33) eher so aus, als hätten sie eine Pol-Linie – eine Folge der von Canters eingesetzten Optimierung. In dieser Hinsicht merkte er an: »This can be interpreted as the ultimate justification for the introduction of a pole line« (»Dies kann als ultimative Begründung für die Einführung einer Pollinie interpretiert werden«), vergaß aber auch nicht, darauf hinzuweisen, dass der W33 auch die Nachteile der flächentreuen pseudozylindrischen Projektionen mit Pollinie zeigt, nämlich die Streckung der äquatornahen Gebiete in Nord-Süd-Richtung bei gleichzeitiger Ost-West-Streckung der hohen Breitengrade.

Nun, ästhetisch gesehen, ziehe ich ohnehin den W34 vor – der übrigens dem Hufnagel 3 nicht unähnlich sieht (Vergleiche Canters W34 mit Hufnagel 3); und wie groß die Ähnlichkeit des W33 zu Projektionen mit echter Pollinie ist, sieht man gut im Vergleich zum Eckert IV – und noch besser im Vergleich zum Hufnagel 10.

Die Ähnlichkeit zu den Hufnagel-Projektionen ist aber auch nicht überraschend, denn sowohl Canters, als auch Hufnagel haben bei in ihren jeweiligen Projektions-Reihen bemüht, Verzerrungen zu reduzieren. Es erscheint also nur logisch, dass ihre Ergebnisse bei flächentreuen Pseudozylindern nicht allzu stark voneinander abweichen.

Zwei weitere Gringorten-Varianten

1972 stellte der Klimatologe Irving I. Gringorten einen flächentreuen Netzentwurf vor, der für die Verwendung in Artikeln und Berichten gedacht war. ^[2] Er entschied sich für einen quadratischen Entwurf, der den zur Verfügung stehenden Raum in Druckerzeugnissen effizient ausnutzt. Der Original-Entwurf ist schon lange auf meiner Website zu finden, aber es gibt auch alternative Arrangements – zum Beispiel kann man jede Hemisphäre in einem Quadrat platzieren. Somit ergibt sich eine rechteckige flächentreue Karte, deren Verteilung von Winkelverzerrungen sich komplett unterscheidet von jenen, die wir von zylindrischen Projektionen kennen.

Wie ich schon an anderer Stelle angemerkt habe, bin ich nicht sehr überzeugt von dem Versuch, einen flächentreuen Netzentwurf in eine rechteckige Karte zu zwingen, aber wenn Du meinst, dass das unbedingt notwendig ist – nun, der Gringorten sieht auf jeden Fall ungewöhnlich aus, aber beachte, dass seine Verzerrungen eigentlich nicht schlimmer ausfallen als in zylindrischen Projektionen wie z.B. dem Smyth equal-surface (der das gleiche Seitenverhältnis hat wie das alternative Arrangement des Gringorten). Unglücklicherweise lässt sich kein Arrangement finden, welches Landmassen in die Bereiche mit den geringsten Verzerrungen platziert, ohne dass es zu massiven Unterbrechungen oder inakzeptablen Verzerrungen anderer Teile der Erde kommt (unten folgt ein Beispiel).

Ich habe mich für zwei Konfigurationen entschieden: Eine äquatorständige, auf 20°W zentriert, die (wie angekündigt) etwas seltsam, aber nicht völlig abwegig aussieht. Die andere sieht nun wirklich seltsam aus… aber irgendwie gefällt sie mir. Sie wirkt äußerst dynamisch und kann als echter »Eye-Catcher« fungieren.

Kramer VII

Der Entwurf Kramer VII wurde 2016 von Leo Murphy ^[3] geschaffen, mit Hilfe der Software Flex Projector. Außer der Auflistung in der Flex-Projector-Galerie wurde (meines Wissens) noch nie irgendwo irgendetwas über diese Projektion geschrieben, das hier ist also sozusagen eine Premiere… :-)

Der Kramer VII wurde für möglichst niedrige Streckenverzerrung optimiert, und tatsächlich zeigt er die niedrigste Durchschnittswerte unter allen Projektionen, die innerhalb des Programms Flex Programms verfügbar sind.

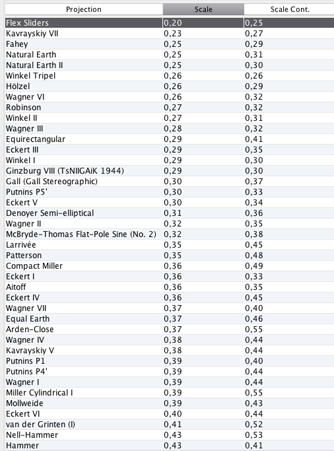Diese Grafik zeigt die Verzerrungstabelle von Flex Projector (nicht alle von FP angebotenen Projektionen haben Platz in diesem Screenshot gefunden). Die Spalte Scale zeigt die Durchschnitts-Streckenverzerrung für den gesamten Globus, die Spalte Scale Cont. berücksichtigt nur kontinentale Bereiche bei der Berechnung des Durchschnitts. Kramer VII hat den niedrigsten Wert in beiden Kategorien.

Die Grafik zeigt nicht alle Projektionen, die Flex Projektionen auflistet, aber hinter dem letzten gezeigten Eintrag (der Hammer-Projektion) folgen nur noch Entwürfe, die einen hoch höheren Wert tragen.

Okay, nun kennen wir eine wichtige Eigenschaft des Kramer VII – können wir ihn jetzt endlich mal sehen?

Zuerst springt mir die ungewöhnliche äußere Form des Entwurfs ins Auge – die einzige mit bekannte Projektion, die in dieser Hinsicht eine entfernte Ähnlichkeit zeigt, ist der Canters W16. Die Zunahme der Flächenvergrößerung zu den Polen hin ist schon beträchtlich, andererseits aber durchaus vergleichbar zu Projektionen wie Eckert III oder Wagner IX und deutlich unter der Vergrößerung von oft genutzten Entwürfen wie Miller Cylindrical oder Gall Stereographic, man kann also sagen, dass die Flächenverzerrung »innerhalb akzeptabler Parameter« liegt, wie Data wohl sagen würde.

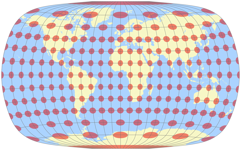
Und da wir gerade von Verzerrungen reden: Hier ist eine Darstellung der Isolinien von Flächen- und maximaler Winkelverzerrung (exportiert von Flex Projector) und natürlich die tissotsche Indikatrix:

Das einzig auffällige Merkmal ist der seltsame Weg, den die Isolinie der Flächenverzerrung von 10° nimmt. Davon abgesehen, sieht eigentlich alles so aus, wie man es von einer Projektion dieser Art erwarten würde. Und um noch einmal auf rechteckige Karten zu kommen: Die äußere Form liegt sehr nahe an der rechteckigen Form, wenn Dir das also wichtig ist, hast Du hier einen guten Kandidaten.

Zusammenfassend kann ich sagen, dass der Kramer VII attraktive ungewöhnliche, aber nicht absolut fremd wirkende Projektion mit niedriger Streckenverzerrung ist. Meiner Meinung nach durchaus benutzbar, also nichts abwegiges.

Bleibt nur noch eine Sache, die angesprochen werden sollte – der Name.
Warum heißt der Entwurf Kramer VII, wenn er von Mr. Murphy geschaffen wurde? Nun, ich habe ihn einfach gefragt, und seine Antwort lautete:

The name was my father’s idea (I let him choose it), and Kramer was the name of our family dog (…)
As for the VII, I’m not sure why my dad picked that. Perhaps because he just liked the number 7? Regardless, there aren’t any Kramers I - VI at the moment. Maybe I’ll have to make them all someday…

Der Name war die Idee meines Vaters (ich habe ihn den Namen wählen lassen), und Kramer lautete der Name unseres Familienhundes (…)
Was die VII angeht, bin ich nicht sicher, warum mein Vater sie gewählt hat. Vielleicht gefiel ihm einfach die Nummer 7? Auf jeden Fall gibt es derzeit keine Kramers I - VI. Eventuell werde ich sie eines Tages erstellen…

Dann wollte ich noch wissen, ob er vielleicht noch eigene Worte zu meiner Vorstellung des Kramer VII hinzufügen möchte, und er hat mich drum gebeten, eine einzige Zeile aufzunehmen (und ich denke, die muss ich nicht übersetzen):

„For my dad.“

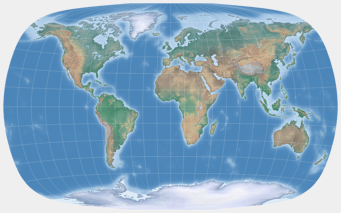
Equal Earth

Und die letzte für heute ist brandneu: Sie wurde erst diesen Monat (August 2018) vorgestellt. ^[4]
Und sie wirkt nicht ungewöhnlich. Im Gegenteil, das erklärte Ziel der Urheber war es, einen Entwurf zu schaffen, welcher der beliebten Robinson-Projektion ähnlich sieht, dabei aber die relative Größe von Flächen beibehält. Es handelt sich also um einen flächentreuen Entwurf, der den prägnanten Namen Equal Earth bekommen hat.

Zugegeben, mein erster Gedanke war: »Was? Warum noch eine pseudozylindrische flächentreue Projektion? Davon haben wir doch schon mehr, als irgendjemand essen kann!«
– aber nachdem ich die Abhandlung der Autoren Šavrič, Patterson & Jenny gelesen hatte, fiel mir auf: So schlecht ist die Idee gar nicht mal.

Ich werde irgendwann demnächst mal näher darauf eingehen.
Für den Moment genießt einfach mal diese ausgewogene Projektion – oder noch besser, lest die (englische) Abhandlung der Urheber, wenn Ihr schon jetzt mehr wissen wollt.

Bis die Tage!

Quellenangaben

↑ Canters, Frank:
Small-scale Map Projection Design.
London & New York 2002.
↑ Ein bisschen mehr über Gringortens Projektion ist zu lesen auf progonos.com (englisch).
↑ Informationen über den Kramer VII entstammen persönlicher Kommunikation mit dem Urheber Leo Murphy.
↑ Šavrič, Bojan & Patterson, Tom & Jenny, Bernhard. (2018):
The Equal Earth map projection. International Journal of Geographical Information Science. 1-12. 10.1080/13658816.2018.1504949. verfügbar auf researchgate.net (Englisch)