Mo, 6.8.2018 Die flächentreuen Strebe-Projektionen von 1992
1992 entwickelte Daniel »daan« Strebe eine Serie von sechs flächentreuen Entwürfen,
indem er bestehende Projektionen modifizierte. Zwei davon sind schon seit längerer Zeit
auf kartenprojektionen.de zu finden, die anderen vier wurden nun hinzugefügt.
Aus diesem Anlass sehen wir uns die komplette Serie einmal etwas genauer an, wobei
ich das Hauptaugenmerk auf die vier neu aufgenommenen Varianten lege.
Soweit ich weiß, ist Strebes eigene Kartenprojektions-Software Geocart das einzige Programm, welches die Projektionen erzeugen kann.
Die Verfahrensweise
Eine detaillierte Beschreibung seiner Verfahrensweise ist verfügbar in Strebes Abhandlung A bevy of area-preserving transforms for map projection designers [1], daher werde ich diesen Punkt möglichst kurz und knapp umreißen.
Wie Strebe in seiner Abhandlung ausführt, kann man die Bonne-Projektion auffassen als eine flächentreue Transformation der Sinusoidal-Projektion, bei der die ursprünglich geraden Parallelkreise unter Beibehaltung ihrer Länge zu Kreisbögen gekrümmt werden. Der Radius der einzelnen Kreise wird beeinflusst durch die Wahl einer Schnittparallele φ1.
Die Bonne-Transformation (nicht zu verwechseln mit der Bonne-Projektion, welche das Resultat der Transformation, angewendet auf die Sinusoidale, darstellt), ist ein Schritt, den Strebe auf bestehende Projektion angewendet hat, um die Serie neuer Projektionen zu erstellen. Bei den »Mutter-Projektionen« handelt es sich um Mollweide, Hammer, Kavraiskiy V, die bereits erwähnte Sinusoidal-Projektion sowie Snyder’s Minimum-Error-Projektionen Pointed Pole und Flat Pole. Abgesehen von der letztgenannten handelt es sich um Projektionen mit punktförmigen Pol – darauf werden wir später noch zu sprechen kommen. Sehen wir uns aber zunächst sein Verfahren im Einzelschritten an, am Beispiel der Mollweide-Projektion.
Zunächst verwendet er eine affine Transformation, um das Projektionszentrum ohne Winkelverzerrungen darzustellen.
Wenn Du nicht weißt, was eine affine Transformation ist, lies Strebes Abhandlung oder schlage es
in der Wikipedia nach.
Im Falle von Kartenprojektionen ist wichtig, dass hierbei eine flächentreue Projektion ihre
Eigenschaft der Flächentreue beibehält.
Die Projektion wird entlang des Äquators unterbrochen, in dem die Bonne-Transformation separat auf die nördliche und die südliche Hemisphäre angewandt wird, was Verzerrungen deutlich verringert. In diesem Schritt wird ein »Krümmungs-Breitengrad« (latitude of curvature) verwendet – dieser entspricht dem Bonne φ1, hier allerdings ohne die Bedeutung einer Schnittparallele in der resultierenden Projektion.
Schließlich werden directional path offsets (was das ist, musst Du bei Strebe nachlesen – ich hab doch versprochen, ich fasse mich kurz) eingesetzt, um die Lücke zu schließen, die durch die Unterbrechung entlang des Äquators entstanden ist. Damit sind wir beim Endergebnis angekommen, welches die Eigenschaft der Flächentreue von der Mutterprojektion übernommen hat.
Die Resultate
Sehen wir uns also erstmal die komplette Serie an: Strebe-Mollweide hatten wir gerade zwar schon, wird hier aus aber noch einmal gelistet, zusammen mit Strebe-Hammer, Strebe-Kavraiskiy-V, Strebe-Sinusoidal, Strebe-Snyder Flat-Pole und Strebe-Snyder Pointed-Pole. Alle gerenderet mit dem Bonne φ1, welches ihnen per Default in Geocart zugewiesen wird:
… und eine persönliche Vorliebe
Und jetzt, hurra! Ich springe auf meine Steckenpferd!
Ich habe schon zwei eigene Experimente gemacht mit Projektionen, die entweder flächentreu sind
oder sich zumindest nicht allzu sehr von der Flächentreue entfernen, und in denen sowohl Afrika,
als auch Grönland eine vernünftige Form zeigen.
Ich rede von dem Versuch, den ich Wagner-Denoyer getauft habe,
und von einer speziellen Konfiguration des Wagner VII/VIII.
(Und wenn Du wissen willst, was ich mit einer »vernünftigen Form« meine, lies den Wagner-Denoyer-Artikel, oder begnüge Dich
mit der Zusammenfassung, dass eine vernünftige Form genau die ist, die mir gut gefällt.)
Nun, dieses Ziel wird von diversen Entwürfen mit punktförmigen Polen ganz leicht erreicht,
z.B. dem Quartic Authalic oder
Crasters Parabolischen Entwurf, aber
ich wollte auch, dass sich die äußeren Meridiane nicht zu sehr krümmen, so dass z.B. Nordamerika
(bei Zentrierung auf den Nullmeridian) nicht so schrecklich verzerrt wird.
Das wiederum schreit nach einer Projektion mit Pol-Linie – aber diese tendieren dazu, Grönland horizontal zu strecken.
Meine Experimente liefen also darauf hinaus, eine vergleichsweise kurze Pollinie zu verwenden,
und den Punkt zu finden, an dem die Verzerrungen einen in meinen Augen tragbaren Kompromiss ausbalancieren.
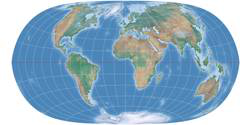
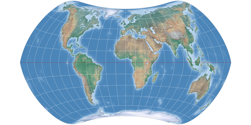
Nun sieh Dir noch einmal Strebes Serie an: Fünf Projektionen weisen punktförmige Pole auf, aber wenigstens drei
von ihnen wirken optisch – in der oben gezeigten Konfiguration – eher wie Entwürfe mit Pollinie, nämlich
Strebe-Mollweide, Strebe-Kavraiskiy-V und Strebe-Snyder Pointed-Pole.
(Bei den beiden letztgenannten ist diese Eigenschaft noch stärker ausgeprägt als beim Strebe-Mollweide.)
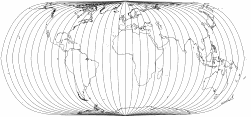
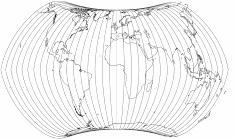
Beachte die folgenden Grafiken:
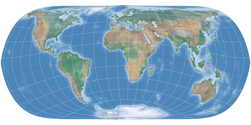
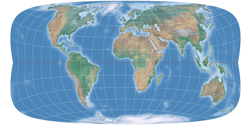
Hier habe ich die äußere Begrenzungslinie der Projektion und die Breitenkreise entfernt, so dass man deutlich sehen
kann, dass die »Pollinie« (die eigentlich keine ist) nur von den Meridianen, die an den Polen zusammenlaufen,
geformt wird. Im Gegensatz dazu ein Entwurf mit echter Pollinie, nämlich der Wagner VII.
Der Unterschied ist deutlich.
Jetzt rufst Du vielleicht: »Ha! In Deinem Wagner-Denoyer sagst Du eindeutig, dass Du eine Pollinie wolltest,
also sind diese Entwürfe aus dem Rennen!«
Tja, nun. Ääähm.
Ich muss zugeben: Als ich den Artikel schrieb, kam es mir einfach nicht in den Sinn, dass es Projektionen
geben könnte, die scheinbar eine Pollinie haben könnten. Und nun muss ich sagen:
Für mich ist das ausreichend!
Strebe-Mollweide, Strebe-Kavraiskiy-V und Strebe-Snyder Pointed-Pole werden also in meine persönliche Liste
der Projektionen, welche in Bezug auf die o.g. Ziele vorteilhaft sind, aufgenommen – besonders die beiden
letztgenannten. Ich kann mich nicht entscheiden, wer von diesen beiden mein Favorit ist, sie haben beide ihre
Vor- und Nachteile.
So.
Nach Behandlung dieser persönlichen Vorliebe kommen wir nun zu Dingen von allgemeinerem Interesse.
Ein paar allgemeine Betrachtungen
Einige Betrachtungen und Anmerkungen zu Strebes Projektionen, in beliebiger Reihenfolge…
– Auffällig sind die Knicke in den Meridianen am Äquator, die alle sechs Projektionen zeigen, ein Resultat des Schließen der Lücke, wie oben gezeigt. Strebe selbst beschreibt sie als unerwünscht, ich selbst muss allerdings sagen, dass ich sie nicht als störend empfinde. Nichtsdestoweniger beeinflussen sie die Verteilung der Verzerrungen (siehe unten).
– Als ich diese Projektionen zum ersten Mal gesehen habe, fand ich, dass ungewöhnlich aussehen.
Mittlerweile habe ich meine Meinung geändert: Ich interessiere mich für Kartenprojektionen (genauso wie
wahrscheinlich Du, denn immerhin liest Du das hier noch). Also bin ich es gewohnt, Projektionen zu betrachten,
ihre Eigenheiten aufzudecken, Unterschiede auszumachen usw.
Aber mal ehrlich, die meisten Leute interessieren sich nicht für dieses Thema oder wissen nicht einmal,
dass es so etwas wie Kartenprojektionen überhaupt gibt. Ich wette, für die meisten dieser Leute sehen zumindest
Strebe-Mollweide, Strebe-Hammer und Strebe-Kavraiskiy-V vollkommen normal aus – so, wie eine Weltkarte eben
auszusehen hat. Vielleicht gilt das sogar für die beiden Strebe-Snyder-Entwürfe.
Nur Strebe-Sinusoidal hat ein wirklich auffälliges Aussehen.
– Fasst man den Strebe-Snyder Pointed Pole in ein Rechteck ein, so hat dieses Rechteck Seitenverhältnisse,
die nahezu denen des Winkel Tripel (originale Version von Oswald Winkel) entsprechen. Wenn Du also mal eine flächentreue Alternative zum Winkel Tripel
suchst: Hier hast Du eine.
(Genauso ähneln die Seitenverhältnisse des umgebenden Rechtecks beim Wagner VII denen von Bartholomews Version
des Winkel Tripel. Das überrascht nicht wirklich, denn Wagner hat seine Projektion explizit als flächentreue Alternative
zum Winkel Tripel entworfen.)
– Da wir gerade vom Strebe-Snyder Pointed Pole sprechen: Diese Projektion ist Strebe’s 1995er Entwurf nicht unähnlich,
was die äußere Form und die Verteilung der Verzerrungen angeht. Man könnte fast vermuten, dass Strebe seine Abwandlung
der Snyder-Projektion so gut gefiel, dass er sich bemüht hat, einen ähnlichen Entwurf zu schaffen, der aber ohne
den Makel der geknickten Meridiane auskommt. Offensichtlich mit Erfolg.
Es ist mir zuvor noch nie aufgefallen, aber auch der Strebe 1995 hat Seitenverhältnisse,
die dem Winkel Tripel sehr nahe kommen.
– Und noch etwas zum Strebe-Snyder Pointed Pole: Mit gefällt die Variante mit Bonne φ1 = 16°N auch sehr gut. Das Seitenverhältnis nähert sich 1:2 an, die Knicke werden abgeschwächt und insgesamt ist sie dem Wagner VII, den ich sehr schätze, nicht unähnlich.
– Um zu zeigen, wie sich der Krümmungs-Breitengrad auf die Projektion auswirkt, zeige ich hier den Strebe-Kavraiskiy-V mit einem Bonne φ1 von 10, 15, 20, 25 und 29 Grad Nord; sowohl in zusammengefügter, als auch unterbrochener Form:
– Eine weitere interessante Konfiguration des Strebe-Kavraiskiy-V zeigt Strebe im Geocart-Handbuch: Zentriert auf 11° Süd und 11° Ost. Mein armes Grönland rutscht dadurch zwar wieder in einen Bereich stärkerer Verzerrungen, dafür werden sämtliche größere Landmassen der Erde inklusive Antarktika unterbrechungsfrei dargestellt.
Das ist natürlich keine besondere Eigenschaft des Strebe-Kavraiskiy-V, sondern kann in gleicher Weise mit allen zylindrischen, pseudozylindrischen und lentikulären Projektionen gemacht werden. Aber da ich gerade dabei war, dachte ich, ich zeige diese Konfiguration mal hier…
Etwas über Rechtecke
Viele Leute scheinen rechteckige Karten zu bevorzugen – schließlich ist das Papier, auf dem sie gedruckt wird, ja auch rechteckig, und man möchte ungern Platz verschwenden. Gerade bei flächentreuen Karten halte ich den Wunsch nach einer rechteckigen Form für äußerst ungünstig. Kurz gesagt: Die Wahl der Projektion sollte meiner Meinung nach durch das, was innerhalb der Karte liegt, bestimmt werden, nicht durch den freien Raum drumherum.
Die rechteckige Form passt nicht gut zu einer flächentreuen Weltkarte. Dennoch verstehe ich den Wunsch, keinen Platz zu verschwenden, also wäre vielleicht eine annähernd rechteckige Karte die richtige Lösung?
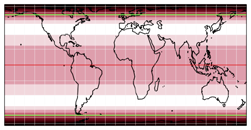
Der Strebe-Kavraiskiy-V in der oben gezeigten Variante ist schon sehr gut in dieser Hinsicht: Meinen Messungen zufolge belegt die eigentliche Karte etwa 89% ihren umgebenden Rechtecks. Vergleiche wir sie mit einer flächentreuen Projektion, die tatsächlich rechteckig ist – der zylindrischen Smyth equal-surface (auch als Craster equal-area bekannt), die ähnliche Seitenverhältnisse zeigt.
Während beim Smyth größere Bereiche der Karte unterhalb von einer Winkelverzerrung von 40° bleiben (gekennzeichnet durch die grüne Line), führt die andersartige Verteilung der Verzerrungen im Strebe-Kavraiskiy-V meiner Meinung nach zu deutlich »natürlicher« wirkenden Formen der Kontinente. Wenn die geplante Verwendung nicht unbedingt nach einer rechteckigen Form schreit, würde ich gerne 11% des zur Verfügung stehenden Raumes opfern, um diese verbesserte Darstellung zu ermöglichen.
Natürlich bin ich mir bewusst, dass man sich in vielen Fällen aus anderen Gründen für einen zylindrischen Entwurf entscheidet, nicht wegen der »Platzverschwendung«, z.B. wegen des rechtwinkligen Gradnetzes. Allerdings haben viele Leute, welche die AuthaGraph-Weltkarte bejubeln, die Tatsache gelobt, dass sie rechteckig ist, was mich vermuten lässt, dass das irgendwie wichtig zu sein scheint…
Southern Comfort
Bisher habe ich alle Konfiguration mit einem Bonne φ1 in der nördlichen Hemisphäre gezeigt, man kann allerdings auch einen Breitenkreis in der südlichen Hemisphäre festlegen. Die entsprechend Resultate sehen m.E. tatsächlich ungewöhnlich aus, aber einige davon nutzen noch mehr als 89% des umgebenden Rechtecks. Andere hingegen sehen einfach interessant aus und mögen das Richtige sein, wenn Du eine Projektion brauchst, die ins Auge springt.
Die Knicke der Meridiane sind natürlich immer noch vorhanden, aber hier biegen sie sich nach innen, was die Projektionen ein wenig so aussehen lässt, als sei der Äquator ein Gürtel… ;-)
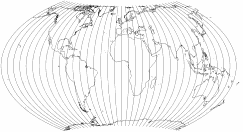
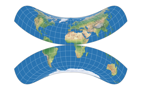
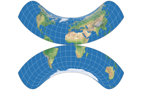
Der Strebe-Sinusoidal mit Bonne φ1 = 26°S zeigt sich »diamantförmig« und eignet sich wohl hauptsächlich für dekorative Zwecke. In dieser Funktion springt er aber sicherlich ins Auge!
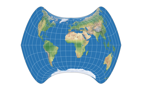
Strebe-Mollweide mit Bonne φ1 = 24°S nähert sich einer rechteckigen Form an, was – siehe oben – ja manchmal hilfreich/gewünscht sein kann. Während das oben gezeigte Beispiel eine »Flächenausnutzung« von ungefähr 89% hatte, sind wir hier schon bei etwa 93% angelangt.
Und dieses Beispiel rückt den Wert sogar auf stolze 97% hoch: Strebe-Hammer, Bonne φ1 = 29°S. Diese Konfiguration hat beinahe die gleichen Seitenverhältnisse wie Gall-Peters, und abermals muss ich sagen, dass in meinen Augen wenig für die zylindrische Projektion spricht.
Und zum letzten Mal (versprochen!) ein kleiner Vergleich zu zylindrischen Projektionen: Strebe-Snyder Flat Pole mit Bonne φ1 = 20°S hat Seitenverhältnisse, die sehr nahe am Behrmann liegen. Okay, zugegeben, es ist sicher nicht die beste Projektion, die ich je gesehen habe, aber ich wollte sie trotzdem in einer »südlichen Variante« zeigen…
Ohne viel weiteres Rumgequatsche, meine beiden Favoriten unter den Konfigurationen mit südlichem Bonne φ1: Mal wieder der Strebe-Kavraiskiy-V, auf 24°S gesetzt…
… und der Strebe-Snyder Pointed Pole, 20°S.
Und zum Abschluss noch ein Vertreter der eher ungewöhnlichen Projektionen:
Strebe-Snyder Pointed Pole mit 35°S.
Es gibt übrigens eine Projektion, die dieser Variante (abgesehen von dessen üblichen Knicken)
nicht ganz unähnlich ist – sowohl, was die äußere Form, als auch was die Verteilung von Verzerrungen
angeht: Die Rede ist von Frank Canters’ W30 (oder auch
Low-error equal-area transformation of Hammer-Wagner [Wagner VII] with twofold symmetry
and a correct ratio of the axes), den ich hier leider nicht zeigen kann
in einem anderen Blogpost zeige.
Wenn Du Canters’ Buch Small-Scale Map Projection Design besitzt, sieh Dir
Figure 5.7 an (S. 215).
Zusammenfassung
Strebes 1992er Serie bietet sechs flächentreue Projektionen, die konfigurierbar sind und sich somit
an viele Anwendungsgebiete (oder persönliche Wünsche) anpassen lassen. Die geknickten Meridiane
sind sicherlich ein gewisses Manko, in der richtigen Konfiguration fallen sie aber kaum auf –
oder lassen sich sogar gewinnbringend einsetzen, sofern man eine auffallende Projektion benötigt.
Verschiedene Konfigurationen nähern sich eine rechteckigen Form an, was manchmal empfehlenswert sein kann.
Natürlich braucht man die Software Geocart, um die Projektionen überhaupt nutzen zu können, was für die meisten Leute wohl ein »Dealbreaker« sein dürfte…
Quellenangaben
-
↑
Strebe, Daniel (2018):
A bevy of area-preserving transforms for map projection designers.
verfügbar auf researchgate.net



























 Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Kommentare
Sei der erste, der einen Kommentar hinterlässt!