Do, 15.4.2021 Die Canters-Projektionen (Teil 2)
Hier ist der zweite Teil meines Schnelldurchlaufs der 2002 vorgestellten Canters-Projektonen.[1] Allgemeine Informationen gab es schon im ersten Teil, also können wir uns ohne großes Rumgequatsche direkt auf die Projektonen stürzen.
Nur zur Erinnerung:
– Alle Canters-Projektionen sind für eine vorteilhafte Darstellung
der Kontinente optimiert, die Ozeane werden dabei nicht berücksichtigt.
Wenn nicht anders angegeben, wird auch Antarktika von der Optimierung ausgeschlossen.
– Ich verwende nicht Canters’ originale Projektionsnamen, sondern die Bezeichnungen, die
Dr. Böhm vorgeschlagen hat.
Pseudozylindrische Projektionen mit Pol-Linie
Was kann ich über sie sagen? Sie sind, ääähmmm…
Sie sind Pseudozylinder. 😉
Der erste, Canters W15, wurde durch Optimierung mit nur einer Einschränkung,
nämlich doppelter Symmetrie, geschaffen. (Abgesehen natürlich von der Einschränkung,
dass das Resultat pseudozylindrisch sein sollte.)
Wie beim polykonischen W12 ist eine Nord-Süd-Streckung der äquatorialen Bereiche
und eine Ost-West-Streckung der hohen Breiten deutlich erkennbar.
Letzteres wird, wie Canters sagt, »leicht verbessert« beim W16, der eine
kürzere Pollinie (halb so lang wie der Äquator) aufweist, die Nord-Süd-Streckung
bleibt jedoch. Sein auffälligstes Merkmal ist, dass die Meridiane zwischen
40° Nord und Süd fast gerade ausgeführt sind, was zu einer charakteristischen
Außenform führt.
Umgekehrt verbessert der W17 (der ein korrektes Längenverhältnis der Achsen zeigt) die äquatorialen Gebiete und erhöht die Streckung der polaren Regionen. Darüber hinaus hat er deutliche geringere Werte an Flächenvergrößerung über die gesamte Karte.
Wie in Teil 1 sehen wir uns am Ende jedes Abschnitts die Tissotsche Indikatrix sowie die K1-Werte an:
| Projektion | K1 |
|---|---|
| Canters W15 | 1,143 |
| Canters W16 | 1,1453 |
| Canters W17 | 1,1458 |
Projektionen mit punktförmigen Polen
»Weltkarten-Projektionen mit einer Pol-Linie von begrenzter Länge zeigen
ausgeglichenere Verzerrungseigenschaften als Projektionen mit punktförmigen Polen«.[2]
It is known. 😉
Aber manchmal werden auch »punktpolige«[3] Projektionen benötigt oder gewünscht
– z.B. für eine realistischere Darstellung; schließlich sind die Pole Punkte auf dem Globus –,
aber die meisten Entwürfe dieser Art wie die
Aitoff-Projektion
zeigen eine starke Kompression der polaren Regionen. Dies wird beim Canters W18
vermieden, und zwar durch die Verwendung einer »apfelschnittförmigen« oder »telophasischen« (wie ich sie mittlerweile nenne)
Projektion nach der Art des
van der Grinten IV,
aber mit deutlich verringerter Flächenvergrößerung.
Ich muss aber sagen, dass mir die Darstellung der Formen und Flächen in den nord-westlichen und nord-östlichen
Bereichen der Karten immer noch ein wenig Bauchschmerzen bereiten…
Daher gefällt mir der Canters W19 besser – obwohl ich, wie Du vielleicht schon gemerkt hast, eher zurückhaltend bin, was das Lob für Pseudozylinder angeht. Die polare Kompression macht sich hier wieder stärker bemerkbar, bleibt aber in erträglichem Rahmen. Er hat die geringste Flächenvergrößerung von allen nicht-flächentreuen Canters-Projektionen: Im Vergleich zum Wert in der Mitte erreicht kein Punkt auf der Karte den Wert von 1,5-facher Vergrößerung.
| Projektion | K1 |
|---|---|
| Canters W18 | 1,1861 |
| Canters W19 | 1,2151 |
Schiefachsige Projektionen
Das Projektionszentrum zu verlegen, ist eine leichte und bekannte Methode, die Verzerrungen auf den Landmassen zu verringern. Entwürfe wie Briesemeister, Philbrick Sinu-Mollweide und Bertin-Rivière nutzen die Möglichkeit, die Kontinenten einfach mal eben in Kartenbereiche zu verlegen, in denen vorteilhafte Verzerrungseigenschaften herrschen. Und hier sind Canters’ Variationen des Themas.
Mit dem Canters W20, zentriert auf 61°N, 24°O, bekommen wir eine weitere Projektion von eher »akademischem« Wert:[4]
Although the re-orientation of the graticule leads to an overall distortion that is much lower than for normal aspect optimisations, the southern part of Africa is split up. The split is caused by the high concentration of land in the Northern Hemisphere, which has more weight in the calculation of the overall distortion value, and therefore strongly influences the position of the centre of the projection.
Obwohl die Neuorientierung des Gradnetzes zu einer Gesamtverzerrung führt, die viel geringer ist als Optimierungen in querachsiger Lage, wird der südliche Teil Afrikas aufgespalten. Die Aufspaltung wird durch die hohe Konzentration der Landmassen auf der Nordhalbkugel verursacht, die bei der Berechnung des Gesamtverzerrungswertes mehr Gewicht hat und daher die Lage des Projektionszentrums stark beeinflusst.
Er schließt, dass der Optimierungsprozess manchmal weiter Anpassungen benötigt, um nützliche Lösungen zu produzieren, setzt das Projektionszentrum auf 45°N, 20°O und optimiert erneut, was im Canters W21 resultiert. Im Vergleich zum W20 zeigt er leicht erhöhte Verzerrungswerte, aber sie bleiben deutlich geringer als für alle seiner Projektionen in querachsiger Lage (abgesehen vom »akademischen« W10).
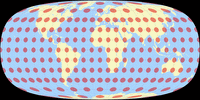
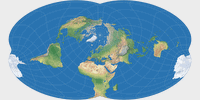
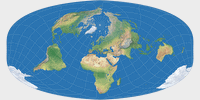
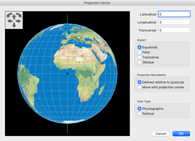
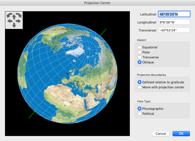
Um alle Kontinente inklusive Antarktika ohne Unterbrechungen zu zeigen, reicht es nicht aus, das Projektionszentrum zu ändern, man muss eine weitere Rotation des Globus vor der Projektion vornehmen. Der Canters W23 wurde definiert mit einem Meta-Pol auf 30°N, 140°W und dem geografischen Nordpol auf einem Meta-Längengrad von 30°O. Dummerweise erlaubt die Projektionssoftware, die ich benutze, keine Angaben wie diese. Stattdessen habe ich das Projektionszentrum auf 48°35′24″ Nord und 9°6′36″ West gesetzt, bei einer Rotation von 40°53′24″ im Uhrzeigersinn. Diese Werte – gefunden von Peter Denner, also abermals herzlichen Dank! – führen beinahe zu den von Canters genannten Angaben zum Meta-Pol usw. Soweit ich das sagen kann, weichen sie weitaus weniger als eine Bogenminute ab.
Um den Prozess zu visualisieren, folgt hier eine Serie von Bildschrimfotos aus Geocart (obgleich das nicht die Software ist, mit der ich die Bilder der Canters-Projektionen erzeugt habe):
Obwohl ich denke, dass dies in jeder praktischen Hinsicht präzise genug ist (und definitiv präzise genug für die Grafiken auf dieser Website), habe ich meine Darstellung des Canters W23 als »Approximation« markiert – nur um sicher zu sein.
Beachte, dass der Entwurf Antarktika zwar ohne Unterbrechungen darstellt, aber nicht mit in die Optimierung der Verzerrungseigenschaften einschließt! Die verbleibenden Kontinente aber werden mit äußerst geringen Verzerrungen dargestellt: Die maximale Winkeldeformation bleibt unter 40° und der Vergrößerungfaktor für beinahe die gesamte Landflächen unter 2,0 – nur das südliche Afrika überschreitet diesen Wert. In meinen Augen verbleibt nur ein kleiner Wermutstropfen: Wie Du vermutlich weißt, nehmen die Landflächen nur knapp 30% der Erdoberfläche ein. Im W23 aber sinkt dieser Wert auf etwa 20% ab. Dies ist natürlich eine direkte Folge davon, dass die unvermeidbaren Verzerrungen so weit wie möglich in die Ozeane verlegt werden – nur so kann die vorteilhafte Darstellung der Landflächen gewährleistet werden. Nichtsdestoweniger ist es in meinen Augen etwas problematisch, wenn eine Projektion, die auf dieses Ziel ausgerichtet ist, die Meere derart aufpumpt.
| Projektion | K1 |
|---|---|
| Canters W20 | 1,0583 |
| Canters W21 | 1,0737 |
| Canters W23 | 1,0506 |
Aber Moment mal – wo ist der W22 geblieben?
Canters zeigt weder eine Grafik, noch listet er die notwendigen Koeffizienten, um ihn zu berechnen,
er erwähnt ihn aber im Text: Es handelte sich um eine Projektion, die dem W23
sehr ähnlich ist und bei den Verzerrungswerten sogar den W10 geschlagen hat.
Leider wurde hier Antarktika leicht unterbrochen – das gewünschte Ziel war also
verfehlt, und Canters hat sie zu Gunsten des W23 verworfen.
Wir haben noch fünf Projektionen übrig – nichtsdestoweniger haben wir hier einen Endpunkt erreicht. Canters hat seine eigenen Projektionen mit einer einigermaßen »exzentrisch« Karte begonnen, die durch uneingeschränkte Optimierung erstellt wurde. Dann hat er verschiedene Einschränkungen hinzugefügt, um praxistauglichere Karten zu gewinnen oder bestimmte Anforderungen zu erfüllen; und beendet die Reihe mit einer sehr speziellen Karte mit beinahe so vorteilhaften Verzerrungseigenschaften, wie sie die erste zeigt.
Flächentreue Transformationen
Für die letzten fünf Entwürfe kehrte Canters zurück zur Optimierung vorhandener Projektionen, aber unter Verwendung einer anderen Vorgehensweise und mit einem leicht veränderten Ziel. Wahrscheinlich, um diese Ausgangssituation widerzuspiegeln, übersprang Dr. Böhm die Bezeichnungen W24 bis W29 und bezeichnete sie als W30 bis W34.
Wenn man minimale Gesamtverzerrungen erreichen will, wird man niemals bei einer flächentreuen Projektion landen: Flächentreue hat immer den Preis von vergleichsweise starken Verzerrungen der Formen. Nichtsdestoweniger ist die Äquivalenz eine nützliche Eigenschaft für viele thematische Karten, für politische Karten, wenn man der Theorie zustimmt, dass political correctness eine Frage der Größe ist – und ja, vielleicht auch für allgemein-geografische Übersichtskarten (und irgendwann werde ich diese Idee weiter ausführen, aber wahrscheinlich nicht in näherer Zukunft).
Aber natürlich kann man sich bemühen, minimale Winkelverzerrungen innerhalb der Klasse der flächentreuen Projektionen zu erreichen – was Canters hier tut. Meiner Meinung nach ist dies die interessanteste Serie der in diesem Blogpost besprochenen Projektionen, deshalb widme ich ihnen ein bisschen mehr Raum.
Vielleicht erinnerst Du Dich an die
Liste der K1-Werte in Teil 1,
in welcher der flächentreue Canters W07 einen sehr guten Wert erreicht hat –
er platzierte sich noch vor verschiedenen vermittelnden Projektionen wie Canters W13 und W14
sowie dem Winkel Tripel Bartholomew. Wie passt das zu meiner Behauptung, dass
dass flächentreue Projektionen keine geringen Gesamtverzerrungen aufweisen können?
Zugegeben: Eigentlich gar nicht.
😳
Für den Moment aber sehe ich den W07 als eine sehr spezielle Ausnahme, die sich
vermutlich durch die Kombination des Messverfahrens und der eigentümlichen
Form des Entwurfs erklären lässt…
Canters Vorgehensweise bei W30 bis W34 unterscheidet sich von den Projektionen, die wir bisher besprochenen haben: Bei den anderen wird die Karte direkt vom Globus projiziert. Hier aber wird der Globus zunächst mittels einer »Elternprojektion« auf die Karte projiziert, welche dann in eine andere Karte transformiert wird. Der Nachteil ist, wie Dr. Böhm anmerkt[5], eine leichte numerische Instabilität. Der Vorteil ist ein höherer Grad der Freiheit in der Gestaltung des Entwurfs: Bei der Verwendung des Umbezifferns (wie bei Canters Wagner-Optimierungen W01 bis W09) kann man der grundlegenden Charakteristik der Elternprojektion nicht entkommen. Diese Einschränkung kann bei der »Post-Transformation« umgangen werden. Die Eigenschaft der Flächentreue allerdings wird in Canters Beispielen beibehalten.
Der Canters W30 ist eine Post-Transformation des Wagner VII – und ein sehr gutes Beispiel für den Unterschied der Vorgehensweisen: Ein Gradnetz wie dieses lässt sich durch Umbeziffern des Wagner VII definitiv nicht einmal annähernd generieren.
Er hat eine markante, ungewöhnliche Außenform
– die einzige mir bekannte Projektion mit einer ähnliches Form
und vergleichbaren Verteilung von Verzerrungen ist der
Strebe-Snyder Pointed Pole, Bonne φ1 = 35°S,
eins meiner eigenen Experimente, das ich vor einigen Jahren vorgestellt habe[6] –, dennoch bin ich der Meinung, dass er, im Gegensatz zum W07, tatsächlich
für die Atlaskartographie oder als Übersichtskarte geeignet ist.
Vielleicht, weil sich seine Form einem Rechteck annähert:
Viele Leute scheinen rechteckige Weltkarten zu mögen, und da Karten
fast immer in einer rechteckigen Fläche gedruckt (oder gezeigt) werden,
verschwendet man nicht viel Platz. Zwar denke ich, dass es
für eine Weltkarte wichtigere Eigenschaften gibt als »geringe Platzverschwendung«,
aber es kann sicher auch nicht schaden, wenn sie über diese Eigenschaft
verfügt, solange sie zusätzlich andere nützliche Merkmale zeigt.
Als flächentreue Projektion mit niedrigen Winkelverzerrungen erfüllt
der Canters W30 diese Bedingung –
mit einem K1-Wert von 1,151 ist er die zweitbeste äquivalente Canters-Projektion nach dem etwas »schwierigem« W07.
Es gibt zwar beachtliche Verzerrungen in der Nähe der Pole und besonders an den äußeren Meridianen, aber die meisten werden von den Kontinentalflächen ferngehalten. Die Streckung in Nord-Süd-Richtung, ein typisches Problem von flächentreuen Entwürfen mit einer Pollinie, ist deutlich verringert. Als Nachteil vermerkt Canters starke Längenverzerrungen entlang des Äquators. Sehen wir uns an, was er dagegen tut…
🌐
Der Canters W31 (ebenfalls eine Wagner-VII-Transformation)
reduziert die Längenverzerrungen entlang des Äquators –
und kehrt zurück zu der typischen Nord-Süd-Streckung. Im Gegensatz zum W30
sieht er überhaupt nicht ungewöhnlich aus. Tatsächlich lässt ihn seine
milde Krümmung der Breitenkreise beinahe wie einen Pseudozylinder aussehen,
z.B. den bekannten Eckert IV:
Canters W31 vs. Eckert IV
Er hat einen höheren (= schlechteren) K1-Wert als der W30, aber nur knapp (1,1588). Welcher von den beiden die bessere Wahl ist, hängt also hauptsächlich von der Frage ab, ob Du eine ungewöhnliche oder eine gewöhnlich aussehende Projektion vorziehst.
🌐
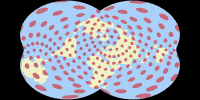
Der Canters W32 ist eine Transformation der Hammer-Projektion und verfügt daher über einen punktförmigen Pol, wobei sich seine Anmutung den Pollinien-Projektionen annähert. Die vom Zentralmeridian entfernten Bereiche werden deutlich weniger stark gekrümmt als bei den bekannten Entwürfen mit punktförmigen Pol. Er gehört zu den wenigen von Canters Entwürfen, die Antarktika beim Optimierungsprozess einschließen.
Mit einem K1-Wert von 1,151 spielt er schon in der Liga von »traditionellen« flächentreuen Projektionen,
allerdings schneidet er für einen punktförmigen Entwurf auch nicht schlecht an.
Wenn Du, aus welchen Gründen auch immer, punktförmige bevorzugst, ist er eine
gute Wahl. Und nebenbei bemerkt – schon wieder haben wir eine Ähnlichkeit
zu Strebes flächentreuen Projektionen von 1992;
er sieht aus wie ein horizontal gestauchter Strebe-Mollweide ohne die
Knicke am Äquator:
Canters W31 vs. Strebe-Mollweide
🌐
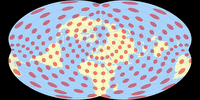
Zum Abschluss präsentiert Canters zwei Transformationen der Sinusoidal-Projektion. Die erste, Canters W33 (K1 = 1,1676) – bei dem Antarktika wieder von der Optimierung ausgenommen wird –, hat eine große Ähnlichkeit zum bekannten Eckert IV und eine noch größere (besonders in Bezug auf die Verteilung der Verzerrungen) zum weniger bekannten Hufnagel 10. Aber interessanterweise verfügt der W33 nicht über eine Pollinie, obwohl es den Anschein hat. Canters merkt an:[7]
Indeed, since the optimisation process start with the sinusoidal projection all meridians in the optimised graticule do meet in one point, only the shape of the meridians has been modified in such a way that it seems as if the graticule really has a pole line. This can be interpreted as the ultimate justification for the introduction of a pole line, as was done by many developers of pseudocylindrical map projections in the last century.
Da der Optimierungsprozess mit der Sinusoidal-Projektion beginnt, treffen sich in der Tat alle Meridiane im optimierten Gradnetz in einem Punkt, nur die Form der Meridiane wurde so verändert, dass es den Anschein hat, als ob das Netz wirklich eine Pollinie hat. Dies kann als ultimative Rechtfertigung für die Einführung einer Pollinie interpretiert werden, wie sie von vielen Entwicklern pseudozylindrischer Kartenprojektionen im letzten Jahrhundert vorgenommen wurde.
Natürlich entgeht es Canters nicht, dass der W33 aufgrund dieser Ähnlichkeit auch die typischen Nachteile der flächentreuen pseudozylindrischen Entwürfe mit Pollinie mit sich bringt, nämlich die Nord-Süd-Streckung äquatorialer und Ost-West-Streckung polarer Regionen. Und so …
🌐
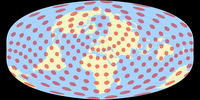
Canters schließt seine Reihe ab mit einem Entwurf, bei dem Antarktika erneut in den Prozess der Optimierung eingeschlossen wird: Der Canters W34. Das hat zur Folge, das er im Vergleich zum W33 eher wie eine der bekannten punktpoligen Projektionen aussieht, auf den ersten flüchtigen Blick scheint aber auch er eine kurze Pollinie zu haben. Es überrascht nicht, dass die Nord-Süd-Streckung weniger aufdringlich ausfällt und die polaren Gebiete weniger verzerrt werden, während die vier »Ecken« benachteiligt werden.
Der W34 hat den schlechtesten Wert an Gesamtverzerrungen von allen Canters-Projektionen. Dies ist leicht damit zu erklären, dass er unter verdammt vielen Einschränkungen erzeugt wurde: Es handelt sich um eine äquatorständige flächentreue pseudozylindrische Projektion mit punktförmigen Polen, bei der Antarktika in die Optimierung eingeschlossen wurde. Wenn man dies berücksichtigt, ist der K1-Wert gar nicht einmal soo schlecht.
Diesmal ist die Tabelle nicht nach den Namen der Projektionen sortiert, sondern nach den K1-Werten, vom besten zum schlechtesten. Sie enthält auch die Elternprojektionen und, zu Vergleichszwecken, den Eckert IV.
| Projektion | K1 |
|---|---|
| Canters W30 ∗ | 1,151 |
| Canters W31 ∗ | 1,1588 |
| Wagner VII ∗ | 1,164 |
| Eckert IV ∗ | 1,167 |
| Canters W33 ∗ | 1,1676 |
| Canters W32 ∗ | 1,2071 |
| Hammer ∗ | 1,214 |
| Canters W34 ∗ | 1,225 |
| Sinusoidal ∗ | 1,263 |
|
∗ flächentreu |
|
Weitere Visualisierungen der Verzerrungen
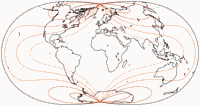
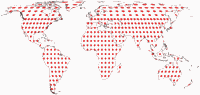
Isolinien der Winkelverzerrungen
Wieder einmal folgen hier Visualisierungen der Verzerrungen, zur Verfügung
gestellt von Peter Denner.
Die Linien werden gezeigt für eine max. Winkelverzerrung von:
10°,
20°,
30°,
40°,
50°,
und 60°.
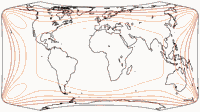
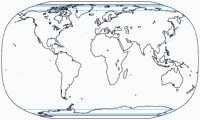
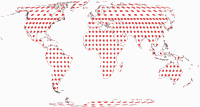
Isolinien der Flächenvergrößerungen
Die flächentreuen Projektionen W30 bis W34 werden hier natürlich
weggelassen. Außerdem fehlt der W19, der so geringe Verzerrungen
hat, dass in der hier verwendeten Konfiguration gar keine Isolinien angezeigt würden
(d.h. alle Punkte auf der Karte bleiben unterhalb einer 1,5-fachen Vergrößerung).
Die Linien werden gezeigt für eine Flächenvergrößerung von:
1,5;
2,0;
2,5;
3,0;
und 3,5.
Bitte beachte, dass sie im Verhältnis zum Wert in der Mitte der Karte gezeigt werden!
Meistens werden sie im Verhältnis zum nominellen Maßstab der Karte gezeigt.
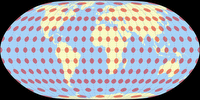
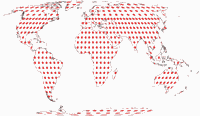
Tissot’sche Indikatrix, nur auf Landmassen
Und die Tissot’schen Indikatrix, begrenzt auf die Kontinentalflächen. Antarktika wird nur gezeigt, wenn es in die Optimierung eingeschlossen war, und beim W23, weil es die Grundidee dieser Projektion war, Antarktika unterbrechungsfrei zu zeigen.
Fazit
So, wir haben uns durch 24 Weltkarten-Projektionen gearbeitet.
Manche von ihnen sind eher akademische Entwürfe mit geringem Praxiswert;
manche sehen etwas ungewohnt aus, aber auch nicht allzu fremdartig;
manche von ihnen verbessern die Verzerrungswerte bekannter Projektionen,
unterscheiden sich optisch aber nicht allzu sehr von bekannten Netzen;
und manche sind auffällige Projektionen von hohem praktischen Wert.
Meine persönlichen Favoriten sind W09, W13 und W14 – naja, wahrscheinlich
würde mir ein W09 mit einer etwas weniger ausgeprägten horizontalen Kompression
besser gefallen, oder ein Entwurf, der zwischen W13 und W14 liegt;
selbst wenn diese etwas schlechtere Verzerrungseigenschaften aufweisen.
Ich bin auch sehr angetan von W30 und W31, sie stellen interessante
Variationen des flächentreuen Themas dar.
Aber alle »nicht-akademischen« Canters-Projektionen sind durchaus ernstzunehmende Alternativen mit geringen Verzerrungswerten.
Inwieweit Canters Bewertungsschema praxistauglich ist, kann und möchte ich nicht beurteilen. Die resultierende Rangfolge finde ich in weiten Teilen nachvollziehbar, manche Platzierungen aber verwundern mich. Seine Entscheidung, nur die Kontinentalflächen (größtenteils unter Ausschluss Antarktikas) in die Bewertung einfließen zu lassen, halte ich für viele Einsatzzwecke für richtig, aber eben nicht für alle. Man muss auf jeden Fall bedenken, dass die Werte nur für den untersuchten Aspekt gelten, und das ist in fast allen Fällen die äquatorständige Ansicht, zentriert auf den Greenwich-Meridian. Schon eine Zentrierung auf 10° Ost, um die Unterbrechung von Ostsibirien zu vermeiden, würde die Rangfolge wahrscheinlich geringfügig ändern – eine Darstellung mit dem Pazifik im Zentrum, wie sie in vielen Ländern der Welt nicht unüblich ist, würde die Liste vermutlich total durcheinander würfeln.
Soweit mir bekannt ist, hat niemand außer Canters selbst jemals den mean finite scale factor K1 zur Bewertung von Kartenprojektionen benutzt. Es ist natürlich möglich, dass mir das nur entgangen ist; nichtsdestoweniger sollte man die Ergebnisliste mit Vorsicht genießen und am besten mit Ergebnissen aus anderen Bewertungsschemata vergleichen.
Liste der K1-Werte
Hier noch einmal eine Liste der K1-Werte, diesmal für alle Canters-Projektionen und den 23 von Canters untersuchten bekannten Projektionen; sortiert vom besten bis zum schlechtesten Wert. Ein Klick auf den Namen zeigt eine Grafik der fraglichen Projektion.
| Projektion | K1 |
|---|---|
| Canters W10 | 1,0465 |
| Canters W23 | 1,0506 |
| Canters W20 | 1,0583 |
| Canters W21 | 1,0737 |
| Canters W11 | 1,1083 |
| Canters W12 | 1,1178 |
| Canters W08 | 1,119 |
| Canters W07 ∗ | 1,121 |
| Canters W13 | 1,1315 |
| Canters W09 | 1,135 |
| Winkel Tripel Bartholomew | 1,142 |
| Canters W15 | 1,143 |
| Canters W16 | 1,1453 |
| Canters W14 | 1,1454 |
| Canters W17 | 1,1458 |
| Canters W06 | 1,146 |
| Wagner IX.i | 1,149 |
| Wagner VIII | 1,149 |
| Canters W30 ∗ | 1,151 |
| Kavrayskiy VII | 1,152 |
| Robinson | 1,154 |
| Canters W31 ∗ | 1,1588 |
| Canters W02 | 1,161 |
| Wagner VII ∗ | 1,164 |
| Wagner II | 1,165 |
| Eckert IV ∗ | 1,167 |
| Canters W33 ∗ | 1,1676 |
| Canters W01 ∗ | 1,169 |
| Wagner VI | 1,177 |
| Wagner I ∗ | 1,179 |
| Wagner IV ∗ | 1,179 |
| Eckert VI | 1,181 |
| Rektangularprojektion φ0 = 30° | 1,181 |
| Canters W18 | 1,1861 |
| Mollweide ∗ | 1,199 |
| Aitoff | 1,201 |
| Flächentreuer Zylinder φ0 = 30° ∗ | 1,203 |
| Canters W32 ∗ | 1,2071 |
| Hammer ∗ | 1,214 |
| Canters W19 | 1,2151 |
| Rektangularprojektion φ0 = 0° | 1,217 |
| Canters W34 ∗ | 1,225 |
| Miller II | 1,228 |
| Miller I | 1,246 |
| Sinusoidal ∗ | 1,263 |
| Flächentreuer Zylinder φ0 = 0° ∗ | 1,272 |
| Mercator | 1,312 |
|
∗ flächentreu |
|
Quellenangaben
-
↑
Frank Canters:
Small-scale Map Projection Design.
London & New York 2002. - ↑ Canters 2002, S. 203.
- ↑ Ich glaube nicht, dass irgendjemand außer Dr. Böhm und mir jemals das Wort »punktpolig« benutzt hat. Es ist aber hilfreich, wenn man nicht ständig die Umschreibung »mit punktförmigen Polen« benutzten möchte… 😉
- ↑ Canters 2002, S. 209.
- ↑ Dr. Rolf Böhm: Canters Low-error Projections I
- ↑ Siehe Blogpost Die flächentreuen Strebe-Projektionen von 1992
- ↑ Canters 2002, S. 218.

































 Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Kommentare
Sei der erste, der einen Kommentar hinterlässt!