Di, 23.2.2021 Die Canters-Projektionen (Teil 1)
Seitdem kartenprojektionen.de ins Netz gestellt wurde, enthielt die Site
eine Reihe von Projektionen von Frank Canters, die 1989 und 2002 vorgestellt worden
sind.[1][2]
Ich hatte immer vor, etwas über sie zu schreiben, aber das habe ich nie getan. 😳
Da ich jetzt sechs weitere Canters-Projektionen hinzugefügt habe, möchte ich
die Gelegenheit beim Schopfe packen und dies nachholen.
Eins möchte ich noch vorausschicken: Ich benutze hier nicht die Namen für die Projektionen, die Canters selbst verwendet hat, sondern die von Dr. Böhm vorgeschlagenen Bezeichnungen.[3] Die Gründe dafür habe ich im Artikel Benennung der Canters-Entwürfe dargestellt.
Die Idee hinter den Canters-Projektionen
Wie ich
kürzlich erwähnt habe,
ist es schwierig, einen einzelnen Wert zu bestimmen, mit dem sowohl
die Flation, als auch die Winkelverformung ausgedrückt werden kann,
weil man versucht, zwei unterschiedliche Arten von Verzerrungen
auf einen gemeinsamen Nenner zu bringen.
Daher wendet Canters eine andere Herangehensweise an:[4]
(…) the general idea (…) is that all types of distortion that occur on maps can be considered the result of a scale distortion that changes continuously with location and direction. Hence global measures that quantify the distortion of finite distances will provide a good overall idea of the extent to which the plane map differs from the surface that is projected.
Die grundlegende Idee ist, dass alle Arten von Verzerrungen, die auf Karten auftreten, als das Ergebnis einer Maßstabsverzerrung betrachtet werden können, die sich kontinuierlich mit Ort und Richtung ändert. Daher liefern globale Maße, die die Verzerrung endlicher Abstände messen, eine gute Gesamtvorstellung davon, inwieweit sich die flache Karte von der projizierten Oberfläche unterscheidet.
Kurz zusammenfasst besteht Canters Vorgehen darin, 5000 zufällig ausgewählte Strecken zu vermessen, deren Start- und Endpunkte auf den Landmassen exklusive Antarktika liegen; sie mit den entsprechenden Strecke auf dem Globus zu vergleichen; die durchschnittliche Verzerrung der Distanzen zu bestimmen und davon den mean finite scale factor (gemittelten finiten Maßstabsfaktor) K1 abzuleiten.
Canters ermittelte den K1-Wert für 23 bekannte Entwürfe.
Was aber hier noch interessanter ist:
Wenn Du einen Wert hast, um die Verzerrungen von Projektionen zu bewerten,
kannst Du auch neue Projektionen entwickeln, die gemäß dieses Wertes
besonders niedrige Verzerrungen aufweisen.
Und ratet mal – genau das hat Canters getan!
Er entwarf verschiedene Projektionen mit niedrigen Verzerrungen auf – und dies ist wichtig, also
wiederhole ich es noch einmal – den kontinentalen Bereichen exklusive der Antarktis.
Bevor wir uns Canters Ergebnisse ansehen, möchte ich versuchen, ein Gefühl für K1 zu vermitteln. Hier ist eine Liste einiger der o.g. bekannten Projektionen und ihrer Werte. Die komplette Liste ist am Ende dieses Blogposts zu finden; für den Moment reicht es aber, die führenden vier, die besten zwei flächentreuen Entwürfe und die beiden letzten (die also die stärksten Verzerrungen aufweisen) aufzuführen.
| Projektion | K1 |
|---|---|
| Winkel Tripel Bartholomew | 1,142 |
| Wagner IX.i | 1,149 |
| Wagner VIII | 1,149 |
| Kavrayskiy VII | 1,152 |
| Wagner VII ∗ | 1,164 |
| Eckert IV ∗ | 1,167 |
| Flächentreuer Zylinder φ0 = 0° ∗ | 1,272 |
| Mercator | 1,312 |
|
∗ flächentreu
Kleinere Werte von K1 sind besser Hinweis: Es ist kein Tippfehler, dass Wagner IX.i und VIII den gleichen Wert aufweisen, das entspricht Canters Angaben. |
|
Die optimierten Wagner-Projektionen
Wie ich in mehreren Artikeln erwähnt habe, hat Karlheinz Wagner eine Methode (das Umbeziffern) entwickelt, seine Projektionen in verschiedenen Hinsichten zu verändern. Canters hat diese Methode genutzt, um jene Variationen der Wagner-Projektionen zu finden, die den niedrigst möglichen Wert von K1 aufweisen (jedenfalls innerhalb der Grenzen des Umbezifferns).
Wir sehen sie uns in zwei Blöcken an.
Zunächst Canters W01, W02 und W06, die Optimierungen der pseudozylindrischen
Wagner I, II und VI (in dieser Reihenfolge):
Was kann ich über sie sagen? Sie sind, ääähmmm…
Sie sind Pseudozylinder.
Hier gibt es nichts Besonderes oder Überraschendes.
Das einzig Bemerkenswerte, das mir einfällt ist, dass sich der
Canters W06 und Frančulas Optimierung des Wagner VI sehr ähnlich sind,
obwohl sie verschiedene Metriken benutzen. Gegenüber den originalen Wagner-Projektionen
verändern sich die Canters-Varianten aber erheblich.
Vergleiche Wagner I und Canters W01
Vergleiche Wagner II und Canters W02
Vergleiche Wagner VI und Canters W06
Vergleiche Frančula XI und Canters W06
Und hier die sind die Darstellungen der Tissotschen Indikatrix sowie die K1-Werte der Originale und ihrer Optimierungen:
| Projektion | K1 |
|---|---|
| Canters W01 ∗ | 1,169 |
| Wagner I ∗ | 1,179 |
| Canters W02 | 1,161 |
| Wagner II | 1,165 |
| Canters W06 | 1,146 |
| Wagner VI | 1,177 |
|
∗ flächentreu |
|
🌐
Weiter mit dem zweiten Block: Die Reihe der lentikulären (oder polykonischen – Canters zieht diesen Begriff vor) ist meiner Meinung nach interessanter. Canters W07, W08 und W09 sind Optimierungen von Wagner VII, VIII und IX. Bei letzterem geht Canters von der Variante aus, die ich Wagner IX.i getauft habe.
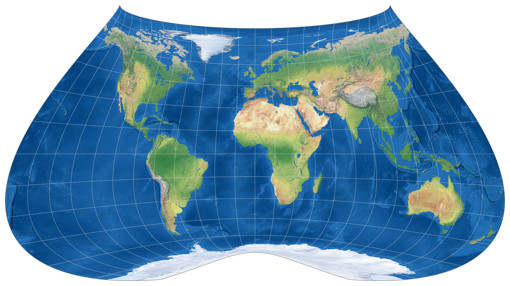
Canters W07 und W08 sehen ungewöhnlich aus – betrachtet man aber nur die kontinentalen Bereiche,
so stellt man fest, dass die Winkelverzerrungen wirklich recht gut aussehen für eine flächentreue Projektion
bzw. eine mit sehr geringen Flächenvergrößerungen. Ihre Form mit der stark gekrümmten
Pollinie schränkt ihre Praxistauglichkeit allerdings ein.
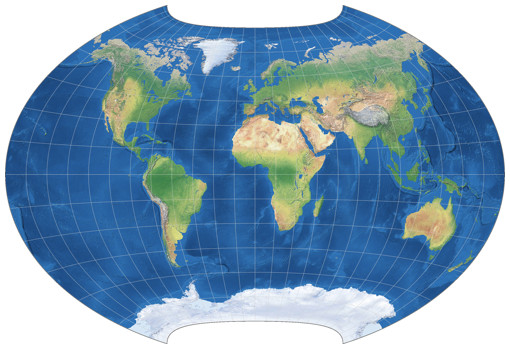
Der W09 hingegen ist m.E. eine gute Wahl für die Atlaskartographie oder allgemein-geografische Weltkarten,
obwohl die Flächenvergrößerungen nahe der Pole doch schon beachtlich wird.
Aber das denke ich eigentlich bei allen Projektionen mit gleichabständigen Breitenkreisen
(entlang des Zentralmeridians).
Hier wieder einige Links, um die Canters-Projektionen zu vergleichen
– mit den Originalen von Wagner und den Optimierungen von Frančula. Hier kommen
Canters und Frančula einmal zu einem ähnlichen Ergebnis, die anderen
drei unterscheiden sich doch deutlich.
Danach dann wieder die tissotsche Indikatrix und die Tabelle mit den K1-Werten.
Canters W07 vs. Wagner VII
Canters W08 vs. Wagner VIII
Canters W09 vs. Wagner IX.i
Canters W07 vs. Frančula V
Canters W07 vs. Frančula XIV
Canters W09 vs. Frančula IV
Canters W09 vs. Frančula XIII
| Projektion | K1 |
|---|---|
| Canters W07 ∗ | 1,121 |
| Wagner VII ∗ | 1,164 |
| Canters W08 | 1,119 |
| Wagner VIII | 1,149 |
| Canters W09 | 1,135 |
| Wagner IX.i | 1,149 |
|
∗ flächentreu |
|
Die polykonischen Low-Error-Projektionen
Bei den bisherigen Beispielen hat Canters existierende Projektionen innerhalb der Möglichkeiten des Umbezifferns für niedrige Verzerrungswerte optimiert. Auf diesem Wege kann man aber den grundlegenden Eigenschaften der Eltern-Projektion nicht entkommen kann und wird daher in den Möglichkeiten der Optimierung beschränkt. Im folgenden Block beginnt er mit einer neuen Projektion, die das Ergebnis einer unbeschränkten Optimierung darstellt, was in einem höchst ungleichmäßigen Entwurf mit niedrigst möglichen Verzerrungswerten resultiert. Dann fügt er nach und nach gewisse Einschränkungen hinzu. Dadurch erhöhen sich die Verzerrungen, aber die Entwürfe bekommen ein konventionelleres Aussehen.
Hier ist also das erste Resultat, der Canters W10. Keine Einschränkungen! Optimier mal los!
Kümmere Dich nicht darum, ob die Karte einsatzfähig sein wird oder nicht!
Habe ich schon erwähnt, dass Canters nur die Kontinentalflächen exklusive Antarktika optimiert? 😉
Dies erklärt die Asymmetrie des Entwurfs:
Die nördliche Hemisphäre enthält etwas mehr
als zwei Drittel der Landmassen der Erde. Daher wird sie in der Kalkulation der
Gesamtverzerrungswerte stärker gewichtet und wird sichtbar besser dargestellt
als die südliche Hemisphere.
Ebenfalls fällt sofort auf, dass Antarktika von der
Optimierung ausgeschlossen wird.
Westliche und östliche Hemisphäre werden ebenfalls asymmetrisch dargestellt,
obwohl dies weniger augenfällig ist.
Der K1-Wert ist 1,0465 –
und wir werden bei den folgenden 17 Projektionen keinen besseren mehr sehen!
Natürlich merkt auch Canters selbst an, dass diese Projektion kaum für eine
fertige Karte geeignet ist. Also fing er an, dem Optimierungsprozess
Einschränkungen hinzuzufügen.
🌐
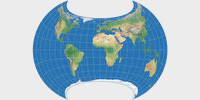
Beim Canters W11 sind die Einschränkungen, dass östliche und westliche
Hemisphäre symmetrisch ausgeführt werden, der Äquator gerade ist und gleichabständig
von den Meridianen geteilt wird.
Das Resultat sieht aus wie… äääähhh… es erinnert mich an… ööhhmmm…
Lassen wir das.
Das Resultat sieht immer noch ungewöhnlich aus, aber in deutlich geringerem Ausmaß als der W10.
Es ist vermutlich nicht geeignet, in einen Atlas aufgenommen zu werden,
aber könnte vielleicht für eine allgemein-geografische Wandkarte genutzt werden –
wenn Du eine Karte willst, die außergewöhnlich aussieht,
geringe Verzerrungswerte aufweist
(K1 = 1,1083),
gleichzeitig aber das Layout der Kontinente beibehält, das man von konventionellen Weltkarten gewohnt ist.
🌐
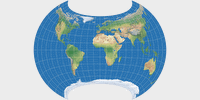
Canters W12: Die nächste Einschränkung ist
die doppelte Symmetrie. Und nun murmele ich »Almost there«
wie der Kerl in Star Wars Ep. IV, denn das sieht schon
sehr wie Weltkarten, die wir gewohnt sind, aus. Canters selber
bemängelt »die erhebliche Verzerrung der Formen in den hohen Breiten
(Ost-West-Streckung) und nahe des Äquators (Nord-Süd-Streckung)«,
aber andererseits ist die äquatornahe Streckung im oft benutzten
Winkel Tripel (Originalversion) fast identisch.
Ich bin nicht besonders begeistert von dieser Projektion, aber
schlecht ist sie sicher nicht.
K1 = 1,1178
🌐
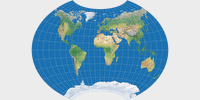
Canters W13: Um die o.g. Mängel des W12 zu beheben, führt Canters eine weitere Einschränkung ein, nämlich gleichabständige Breitenkreise. Projektionen dieser Art, so führt er an, »bieten ein gutes Gleichgewicht zwischen den Verzerrungen von Winkeln und Flächen und haben aufgrund der fehlenden Maßstabsvariation entlang des Mittelmeridians eine angenehme Wirkung auf die Gesamtdarstellung der Kontinente«.
Das Resultat hat, abgesehen von der Pollinie,
eine gewisse Ähnlichkeit mit dem originalen Winkel Tripel:
Canters W13 vs. Winkel Tripel
Den K1-Wert listet Canters leider nur für den Winkel Tripel Bartholomew auf,
er entspricht 1,142 und bleibt hinter dem W13 mit K1 = 1,1315 zurück.
🌐
Canters W14:
Letztendlich wird die Länge der Achsen angepasst, so dass der Äquator
und der Zentralmeridian im korrekten Verhältnis von 2:1 zueinander stehen.
Im Vergleich zu dem W13 verbessert das sie Formen in äquatornahen Gebieten,
allerdings auf Kosten einer stärkeren Ost-West-Dehnung der hohen Breiten,
und Canters schließt:
»Welcher der beiden Entwürfe vorzuziehen ist, wird vom persönlichen Urteil
des Kartenmachers abhängen.«
Der W14 (K1 = 1,1454)
wurde in verschiedenen belgischen Publikationen genutzt, und wenn
Du irgendwo einen Verweise auf die Canters-Projektion findest,
dann ist damit der Canters W14 gemeint.
Für mich sind sowohl der W13, als auch der W14 großartige Entwürfe, die eine gute Wahl für Atlaskartographie und allgemein-geografische Weltkarten darstellen. Es erstaunt mich, dass ihre K1-Werte hinter denen von W07 und W08 zurückfallen. Natürlich, der W08 hat geringere Größenverzerrungen als W13 und W14, und der W07 zeigt gar keine Vergrößerungen – trotzdem hätte ich hier ein anderes Ergebnis erwartet. Wie auch immer, das außergewöhnliche Erscheinungsbild von W07 & W08 steht der Verwendung in den genannten Einsatzgebieten wohl im Wege.
Weitere Visualisierungen der Verzerrungen
Wenn man über Projektionen mit niedrigen Verzerrungswerten spricht, ist es hilfreich, die Verzerrungen auch zu visualisieren. Eine Variante haben wir oben schon gesehen, die Tissot’sche Indikatrix. Aber hier folgen noch weitere!
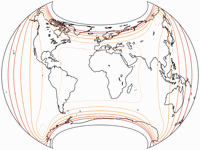
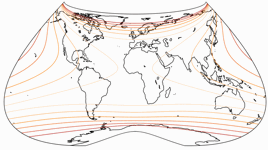
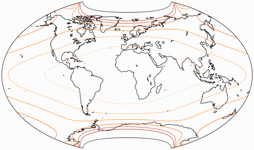
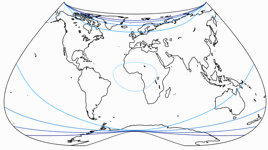
Isolinien der Winkelverzerrungen
Leider habe ich nicht die notwendigen Tools, mit denen ich
Grafiken, welche die Isolinien der Verzerrungen zeigen, erzeigen kann.
(Jedenfalls nicht für die meisten der Projektionen, die in diesem
Blogpost besprochen werden.)
Peter Denner ist eingesprungen und hat mir die Grafiken für
Canters W07 bis W14 (minus dem W10) zugeschickt.
Also abermals: Thank you, Peter! 🙏
Die Isolinien werden gezeigt für eine maximale Winkelverzerrung von:
10°,
20°,
30°,
40°,
50°,
und 60°.
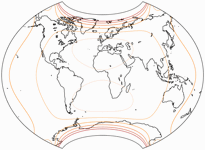
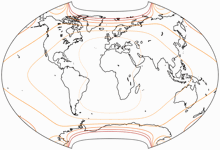
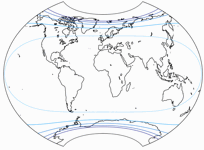
Isolinien der Flächenvergrößerungen
Abermals stammen die folgenden Grafiken von Peter.
Da der Canters W07 flächentreu ist, können wir ihn hier weglassen.
Die Linien werden gezeigt für eine Flächenvergrößerung von:
1,5;
2,0;
2,5;
3,0;
und 3,5.
Bitte beachte, dass sie im Verhältnis zum Wert in der Mitte der Karte gezeigt werden!
Meistens werden sie im Verhältnis zum nominellen Maßstab der Karte gezeigt.
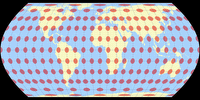
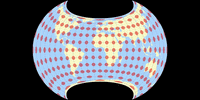
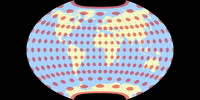
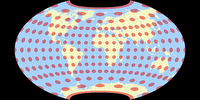
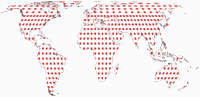
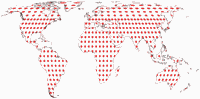
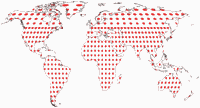
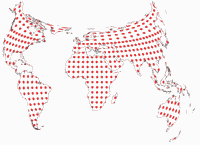
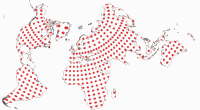
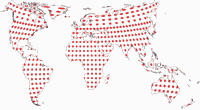
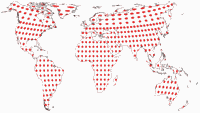
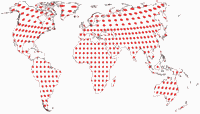
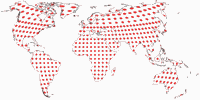
Tissot’sche Indikatrix, nur auf Landmassen
Und noch eine Darstellung der Tissot’schen Indikatrix:
Da Canters nur auf Landmassen exklusive Antarktika optimiert hat (das habe ich erwähnt, oder?),
halte ich es für hilfreich, die Tissot-Ellipsen auch nur in den optimierten Bereichen zu zeigen.
Keine Ablenkung durch die Verzerrungen in den Ozeanen oder die exzentrische Außenform der Karte.
Hier ist die komplette Reihe aller Projektionen, die wir in diesem Blogpost besprochen haben:
Liste der K1-Werte
Wie oben versprochen, folgt zum Abschluss die Liste der Werte von K1, die Canters für 23 bekannte Projektionen ermittelt hat, plus den Werten der bisher genannten Canters-Projektionen; sortiert vom besten bis zum schlechtesten Wert:
| Projektion | K1 |
|---|---|
| Canters W10 | 1,0465 |
| Canters W11 | 1,1083 |
| Canters W12 | 1,1178 |
| Canters W08 | 1,119 |
| Canters W07 ∗ | 1,121 |
| Canters W13 | 1,1315 |
| Canters W09 | 1,135 |
| Winkel Tripel Bartholomew | 1,142 |
| Canters W14 | 1,1454 |
| Canters W06 | 1,146 |
| Wagner IX.i | 1,149 |
| Wagner VIII | 1,149 |
| Kavrayskiy VII | 1,152 |
| Robinson | 1,154 |
| Canters W02 | 1,161 |
| Wagner VII ∗ | 1,164 |
| Wagner II | 1,165 |
| Eckert IV ∗ | 1,167 |
| Canters W01 ∗ | 1,169 |
| Wagner VI | 1,177 |
| Wagner I ∗ | 1,179 |
| Wagner IV ∗ | 1,179 |
| Eckert VI | 1,181 |
| Rektangularprojektion φ0 = 30° | 1,181 |
| Mollweide ∗ | 1,199 |
| Aitoff | 1,201 |
| Flächentreuer Zylinder φ0 = 30° ∗ | 1,203 |
| Hammer ∗ | 1,214 |
| Rektangularprojektion φ0 = 0° | 1,217 |
| Miller II | 1,228 |
| Miller I | 1,246 |
| Sinusoidal ∗ | 1,263 |
| Flächentreuer Zylinder φ0 = 0° ∗ | 1,272 |
| Mercator | 1,312 |
|
∗ flächentreu |
|
Irgendwann demnächst …
In Teil 2 werden wir die Projektion W15 bis W21, W23 und W30 bis W34 besprechen.
Bis dann!
Quellenangaben
-
↑
Frank Canters:
New Projections for World Maps, a Quantitative Perceptive Approach.
Cartographica, 26, 53 - 71, 1989.
doi.org/10.3138/6212-46V4-655U-766K (Paywall) -
↑
Frank Canters:
Small-scale Map Projection Design.
London & New York 2002. - ↑ Dr. Rolf Böhm: The Canters Index
- ↑ Canters 2002, S.92.

















 Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Kommentare
Sei der erste, der einen Kommentar hinterlässt!