Fr, 1.1.2021 14 Projektionen für 2021 (Intro)
Jedes Jahr mache ich mir einen kleinen Kartenprojektions-Kalender – ausführlich
habe ich davon schon letztes Jahr geschrieben.
Dieses Jahr hatte ich ein gewisses Problem, was ich vor einem Jahr schon angesprochen habe.
Ich zitiere:
(…) ich bemühe mich, einen interessanten Mix aus unterschiedlichen Entwürfen zusammenzustellen. Optisch unterschiedlich, aber auch aus unterschiedlichen Gruppen und mit unterschiedlichen Eigenschaften. Und ich versuche, mich nicht allzu sehr zu wiederholen. Ich wähle also keine Projektionen aus, die ich schon in den Vorjahren gezeigt habe – es sei denn, ich zeige ein anderen Aspekt oder eine andere Konfiguration.
Das macht es mittlerweile natürlich etwas schwierig, noch 12 zu finden. Sicher, es gibt hunderte von Projektionen, aber ich muss z.B. auch wirklich nicht alle pseudozylindrischen Entwürfe durchhecheln.
Was die Auswahl weiter einschränkt, ist dass ich nur Entwürfe nehmen möchte, die mir optisch gefallen oder wenigstens auf irgendeine Weise interessant sind. Dieses Jahr dachte ich mir, dass es nun wirklich nicht mehr ohne Wiederholungen geht – dass ich nun doch die eine oder andere Projektion zeigen müsste, die ich vor ein paar Jahren schon einmal hatte. Wenigstens wollte ich die aus dem letzten Jahr vermeiden; und die wiederholten mit einem anderen Kartenbild als damals zeigen.
Und dann dachte ich: Wenn es schon Wiederholungen geben muss, dann lass es wenigstens einen guten Grund dafür geben! So kam ich auf die Idee, Projektionen zu zeigen, die besonders niedrige Verzerrungswerte aufzeigen. Und nun fühle ich mich genötigt, noch etwas zu schreiben:
Eine kurze Einleitung über Verzerrungen und ihre Messverfahren
Alle Kartenprojektionen haben Verzerrungen. Die einen verzerren Größenverhältnisse, andere die Formen, viele verzerren beides. Das Ausmaß der Verzerrungen ändert sich über die Karte hinweg: Irgendwo auf der Karte gibt es einen Punkt, der keine oder nur geringe Verzerrungen hat – und je weiter man sich von diesem Punkt hinweg bewegt, desto größer werden die Verzerrungen. Die Variation im relativen Flächenmaß (die Flation) lässt sich gut messen; sowohl für einen einzelnen Punkt auf der Erdoberfläche, als auch in Gestalt eines Durchschnittswerts für die ganze Karte. Gleiches gilt für die Abweichungen von den Formen, die sog. Winkelverformung.
Gerne hätte man einen einzigen Wert, in den Flation und Winkelverzerrungen einfließen, so dass man von dieser oder jener Projektion sagen kann: Diese Projektion die niedrigsten Gesamtverzerrungen von allen. Aber das ist nicht einfach: Wie bringt man zwei unterschiedliche Arten der Verzerrung auf einen gemeinsamen Nenner? Das geht nur, indem man willkürliche Entscheidungen fällt, wie sie gegeneinander aufzuwiegen sind. Und so wurden verschiedenartige Metriken (Messverfahren) entwickelt. Jede davon hat seine Vor- und Nachteile. Jede stuft die Gesamtverzerrung diverser Projektionen anders ein. Ein Kartenschöpfer kann eine bestehende oder eine neu geschaffene Projektion dahingehend modifizieren, dass sie nach einer dieser Metriken besonders niedrige Verzerrungswerte aufweist, eine sog. Optimierung. Wendet man ein anderes Messverfahren an, kann der gleiche Entwurf höhere Werte zeigen.
Alle Karten dieses Kalenders haben niedrige Verzerrungswerte nach dem einen oder anderen Messverfahren, manche sind Optimierungen. Und weil verschieden gemessen wird, sehen auch die resultierenden Projektionen höchst unterschiedlich aus.
Nun, das war eine sehr kurze Einführung in die Thematik der Verzerrungen.
Wenn Du mehr wissen willst, gehe zu daan Strebes exzellentem Posting
On distortion and optimal projections
und lies mindestens bis zum Satz:
“Nevertheless, we really seem to want answers about which projection is better, so we keep trying.“
(Leider nur in Englisch verfügbar. Gegebenenfalls empfehle ich, das Posting häppchenweise in den Online-Übersetzer
DeepL einzukopieren – das Ergebnis ist nicht perfekt, aber gut
genug, um es zu verstehen.)
Auf jeden Fall habe ich nun einen guten Grund für die wiederholten Kandidaten:
Sie dürfen in einer Auflistung von Projektionen mit niedrigen Verzerrungswerten
einfach nicht fehlen.
Problem gelöst! 😉
Das Titelbild des 2021er Kalenders
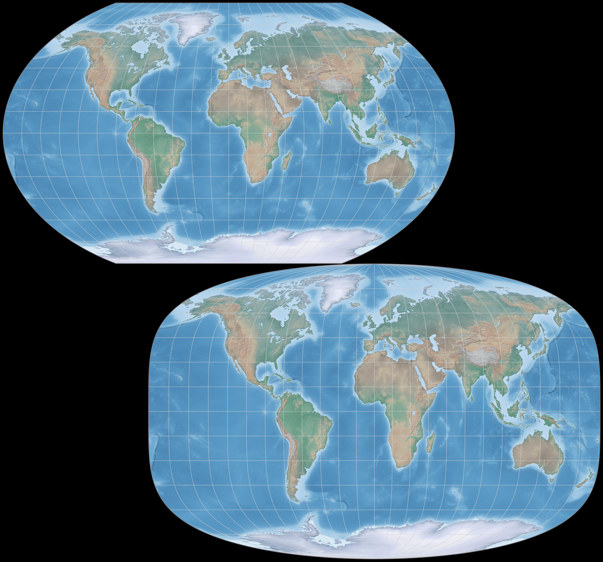
Nachdem ich mich für das Thema des Kalender entschieden hatte, begann ich, passende Projektionen auszuwählen, und schon bald hatte ich 18 ausgewählt. Also habe ich einige aussortiert und als ich dann die endgültigen zwölf hatte, fiel mir auf, dass es 11 lentikuläre Projektionen und eine aus der Gruppe der »Verschiedenen« war. Ich dachte mir, dass ich wenigstens eine oder zwei pseudozylindrische aufnehmen sollte – und um zu vermeiden, noch einmal in den Entscheidungsprozess gehen zu müssen, habe ich es mir einfach gemacht und sie einfach aufs eingangs gezeigte Titelbild gesetzt.
Es zeigt einen Klassiker – den Kavraiskiy VII, 1939 entworfen von Vladimir V. Kavraiskiy –
und einen modernen Entwurf, den the Györffy A (János Györffy, 2018).
Beide haben gleichabständige Breitenkreise, aber während der Kavraiskiy VII
mit Pollinie ausgeführt wird, verfügt der Györffy A über punktförmige Pole.
Da Kavraiskiys Projektion schon vor 80 Jahren vorgestellt wurde, überrascht es nicht, dass sie schon
nach diversen Messverfahren untersucht worden ist:
- Sie erreichte im Jahr 2001 Platz 6 in einer Liste von 100 Projektionen, sortiert nach Richard Capeks Verzerrungswert Q; [1]
- Platz 4 in einer Liste von 23 bekannten Projektionen, sortiert nach dem »mean finite scale factor« K1; [2]
- Platz 3 unter den von Goldberg & Gott (2007) aufgeführten sechs »Projektionen mit dem niedrigsten Wert von ∑ε« (einem Beispiel, wie man Verzerrungseigenschaften in einem einzigen Wert zusammenfassen kann, wobei deutlich auf die Probleme bei dieser Vorgehensweise hingewiesen wird); [3]
- ebenfalls Platz 3 in sowohl Frančulas (1971) Liste von 10 oft benutzten Entwürfen, sortiert nach dem Airy-Kavraiskiy-Kriterium EAK; [4]
- als auch in Györffys Liste mit dem verwandten EK-Wert von 18 bekannten Projektionen. [5]
Györffys Projektion wurde erst in der letztgenannten Abhandlung von 2018 vorgestellt, daher gibt es (soweit ich weiß) bisher nur den Verzerrungswert, den Györffy selbst genannt hat: Györffy A erreichte EK = 0.36756, womit er den Kavraiskiy VII mit EK = 0.3693 knapp überholt hat (niedrige Werte sind hier besser).
Man kann also beruhigt feststellen, dass beide Projektionen die Anforderung der niedrigen Verzerrungswerte erfüllen.
Die Projektion für Januar wird ein weiterer Klassiker sein.
Bis bald!
Quellenangaben
-
↑
Richard Capek, 2001:
Which is the Best Projection for the World Map?
icaci.org/files/documents/ICC_proceedings/ICC2001/icc2001/file/f24014.pdf -
↑
Frank Canters:
Small-scale Map Projection Design.
London & New York 2002. -
↑
Goldberg & Gott, 2007:
Flexion and Skewness in Map Projections of the Earth
physics.drexel.edu/~goldberg/projections/goldberg_gott.pdf - ↑ Nedjeljko Frančula, 1971: Die vorteilhaftesten Abbildungen in der Atlaskartographie
-
↑
János Györffy, 2018: Minimum distortion pointed-polar projections for world maps by applying graticule transformation
doi.org/10.1080/23729333.2018.1455263
Mein Kartenprojektions-Kalender 2021
Um einen anderen Teil der Serie meines 2021er Kartenprojektions-Kalenders zu lesen, wähle den gewünschten Monat aus.













 Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Kommentare
Sei der erste, der einen Kommentar hinterlässt!