14 Projektionen für 2021 (Teil 3)

Mo, 1.3.2021 14 Projektionen für 2021 (Teil 3)

Wenn Du Dich wunderst, worum es hier überhaupt geht, hast Du das Vorwort wahrscheinlich nicht gelesen.

März: Winkel Tripel Bartholomew

Winkel Tripel Bartholomew
Urheber	Oswald Winkel (1921)
Gruppe	Lentikulär
Eigenschaft	Vermittelnd
Andere Namen	Winkel Tripel Times Atlas Winkel Tripel φ₀ = 40°
Anmerkungen	Diese Version wurde von John Bartholomew ca. 1955 entworfen, sie verwendet 40° Nord/Süd als Schnittparallele (anstelle der 50°28´ in Winkels Originalentwurf).

Diesen Monat haben wir einen echten Klassiker: Den Winkel Tripel (in der Bartholomew-Variante), der in Atlanten, auf Wandkarten oder thematischen Karten in Nachrichtenmagazinen usw. regelmäßig zum Einsatz kommt.
Darüber hinaus – und das ist wichtiger in Bezug auf das Thema dieses Kalenders – gehört er stets zu den besten Projektionen gemäß mehrerer der Messverfahren, die ich in der Einleitung erwähnt habe. Und meistens wird er sogar als der beste Entwurf unter den »bekannten« Projektionen gelistet (womit normalerweise diejenigen gemeint sind, die entwickelt wurden, bevor man mit Hilfe von Computern Low-Error-Projektionen berechnen lassen konnte). Die gilt sowohl für den originalen Winkel Tripel, als auch für die Bartholomew-Variante.
Vergleiche Winkel Tripel Original und Winkel Tripel Bartholomew

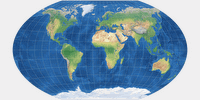
Normalerweise werden beide Varianten in ihrer »schüsselförmigen« Form gezeigt; aber oben sieht man eine rechteckige Form: Ich habe hier eine Darstellung gewählt, die man oft (wie ich im Februar 2020 erwähnt habe) beim van der Grinten I zu sehen bekommt: Die Projektion wird über ihre üblichen Begrenzungen hinaus erweitert, indem bestimmte Teile der Welt im Osten und Westen wiederholt werden, bis ein Rechteck vollflächig ausgefüllt wird.

Ich muss sagen, dass ich von dieser Herangehensweise nicht allzu begeistert bin – allerdings hatte ich beide Winkel-Tripel-Varianten schon in vorhergehenden Kalendern, also wollte ich diesmal wenigstens eine andere Darstellungsweise zeigen.
Ich denke, ich müsste nicht einmal erwähnen, dass die vorteilhaften Merkmale der Verzerrungen nur innerhalb der üblichen schüsselförmigen Begrenzungen zu beobachten sind, während in den wiederholten Teilen erhebliche Verzerrungen auftreten.

Das wär’s für diesen Monat… Warte mal, hatte ich nicht versprochen, dass der Blogpost dieses Monats deutlich länger sein würde?
Hatte ich. Aber ich habe es mir anders überlegt und entschieden, dass es doch besser ist, die anderen Sachen, die ich noch sagen wollte, in einem eigenen Blogpost zu veröffentlichen. Ich habe die Arbeit daran schon angefangen, also wird er hoffentlich sehr bald verfügbar sein.

Nächsten Monat sehen wir dann eine der o.g. Low-Error-Projektionen, die mit Hilfe des Computers erstellt worden sind.

Quellenangaben

↑ János Györffy, 2018: Minimum distortion pointed-polar projections for world maps by applying graticule transformation
doi.org/10.1080/23729333.2018.1455263