Cupola-Projektion und der Asymmetrische Wagner VII.b

Di, 14.12.2021 Cupola-Projektion und der Asymmetrische Wagner VII.b

Die Landmassen der Erde sind nicht gleichmäßig über den Globus verteilt – so enthält die nördliche Hemisphäre rund zwei Drittel der gesamten Landfläche. Noch wichtiger: Nutzt man eine Projektion in der üblichen äquatorständigen Ansicht, ist es in der nördlichen Hemisphäre unmöglich, alle Kontinentalflächen von den Rändern der Karte fernzuhalten, wo meistens die stärksten Verzerrungen zu finden sind. Es gibt drei Methoden, mit diesem Problem umzugehen:

Man kann eine unterbrochene Projektion verwenden, bei der die Unterbrechungen so gesetzt sind, dass Verzerrungen möglichst gut von den Landflächen ferngehalten werden. Das bekannteste Beispiel dieser Art dürfte Goodes Homolosine sein (die natürlich Grönland durchschneidet, weshalb sie manchmal mit einer kleinen Erweiterung versehen wird, um dieses Problem zu umgehen – wie es Mr. Furuti früher auf seiner schmerzlich vermissten Website gezeigt hat).
Man kann sich für ein anderes Kartenzentrum entscheiden, um sich von der üblichen äquatorständigen Ansicht zu verabschieden und die Landflächen somit in Kartenbereichen mit niedrigeren Verzerrungswerten zu platzieren, wie es z.B. in der Briesemeister-Projektion getan wurde.
Oder man entscheidet sich für eine asymmetrische Projektion, mit der man der nördlichen und der südlichen Halbkugel eine unterschiedliche Form und somit eine unterschiedliche Verteilung der Verzerrungen verpasst – womit wir beim Thema wären. Am Vergleich des symmetrischen Strebe 1995 mit seinem asymmetrischen Bruder von 2011 lässt sich sehr gut erkennen, wie die Asymmetrie dazu führt, beide Hemisphären mit einer vorteilhaften Verteilung von Verzerrungen zu versehen:

Man kann die o.g. Methoden natürlich auch kombinieren: Der Bertin-Rivière verwendet Asymmetrie und ein anderes Kartenzentrum, Cahill-Concialdi kombiniert Asymmetrie mit Unterbrechungen, und Danseiji IV benutzt sogar alle drei Methoden. Die beiden Projektionen, die wir uns ansehen, verwenden allerdings Asymmetrie als einzige Methode – sie sind nicht unterbrochen und zeigen die gewohnte äquatorständige Ansicht.

Cupola-Projektion

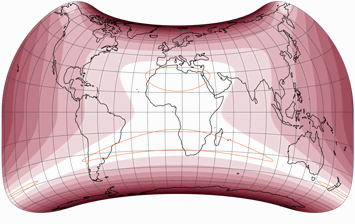
Bei den meisten flächentreuen Projektion verläuft die Verteilung der Winkelverzerrungen so: Die geringste Menge an Verzerrungen findet man bei oder in der Nähe von der Kartenmitte, sie erhöht sich dann langsam zum Rand der Karte hin – wie man oben am Strebe-Beispiel sehen kann. Die Cupola-Projektion, vorgestellt im März 2021 von Weia Reinboud^[1]^[2] (und seit heute auch auf meiner Website zu finden) verwendet aber eine andere Herangehensweise.

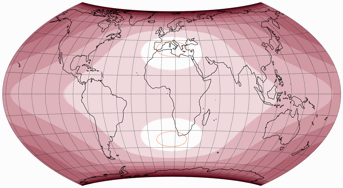
Sie zielt nicht darauf ab, so viel Landfläche wie möglich mit so geringen Verzerrungen wie möglich abzubilden. Stattdessen bemüht sie sich, die Verzerrungen auf den Kontinentalflächen (mit Ausnahme von Antarktika) am Rand der Karte zu reduzieren – also genau dort, wo die Winkelverzerrungen normalerweise am stärksten ausfallen. Unglücklicherweise ist die einzige Art der Verzerrungs-Visualisierung, die ich für diese Projektion erzeigen kann, die oben gezeigte Tissot’sche Indikatrix. Die Grafiken auf der Website von Frau Reinboud zeigen viel besser, wie gut das geplante Ziel in Vergleich zu anderen Projektionen erreicht wird. Ich kann nur wärmstens empfehlen, diese gründlich zu studieren!

Der begrenzende Meridian der Cupola-Projektion wurde auf 168°58′37″ West festgesetzt (dort liegt auch ein Teil der Datumsgrenze), um keine größeren Landflächen (außer Antarktika) zu durchschneiden. Der Zentralmeridian liegt daher auf 11°01′23″ Ost.
Beachte, dass die Projektion für niedrige Verzerrungen mit diesem Projektionszentrum optimiert wurde – das Zentrum auf z.B. den Greenwich-Meridian zu verlegen, würde die vorteilhaften Verzerrungswerte zu einem gewissen Grad zunichte machen.

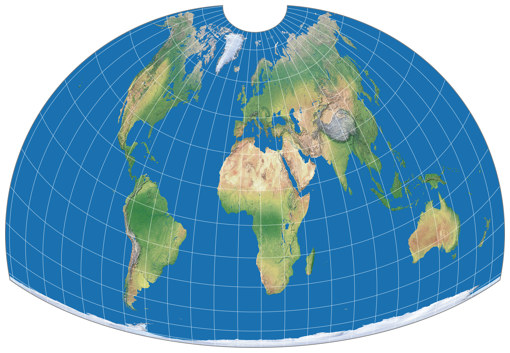
Die Cupola-Projektion ist, soweit ich weiß, die erste Projektion überhaupt, welche auf die Reduzierung von Verzerrungen nahe der Ränder der Karte abzielt. Das Ergebnis sieht ungewöhnlich, aber meiner Meinung nach auch sehr ansprechend aus. Die kompakten Seitenverhältnisse – grob 1:1,46 – bieten sich an für thematische Karten (sofern diese flächentreu sein sollten); aber auch als dekorative Wandkarte kann sie punkten.

Wagner VII.b Asymmetrisch

In meinem Happy Birthday, Wagner VII Blogpost habe ich den Asymmetrischen Wagner VII.b präsentiert und versprochen, noch einmal etwas ausführlicher auf diese Projektion einzugehen.
Dieses Versprechen möchte ich nun einlösen.

Ich habe schon im Mai-Artikel meines 2020er Kartenprojektionen-Kalenders einen Entwurf namens Asymmetrischer Wagner VII gezeigt. Diesen habe ich aber nun noch einmal etwas modifiziert. Zunächst möchte ich noch einmal kurz wiederholen, was ich letztes Jahr schon sagte:

– 1941 stellte Karlheinz Wagner die Projektion vor, die wir heute Wagner VII nennen. Ein flächentreuer Entwurf, der (wie ich schon mehrfach erzählt habe) anpassbar ist, nämlich in Bezug auf die Länge der Pol-Linie, die Krümmung der Breitenkreise und das Längenverhältnis der Hauptachsen.

– 2019 entwarf John J. G. Savard eine asymmetrische Wagner-Variante unter Verwendung der von Wagner gebotenen Konfigurations-Parameter, allerdings mit unterschiedlichen Einstellungen für die nördliche und die südliche Hemisphäre. Er zeigte sein Resultat auf seiner eigenen Website (englisch; fast am Ende der verlinkte Seite) und im (ebenfalls englischen) Mapthematics Forum. Gerendert wurden diese Grafiken von seiner selbst geschriebenen und nur privat benutzten Kartenprojektions-Software.
John erklärte, er sei vom oben erwähnten Strebe 2011 inspiriert.

– Und 2020 habe ich dann eine Approximation von Johns Entwurf in meinen Kalender aufgenommen.

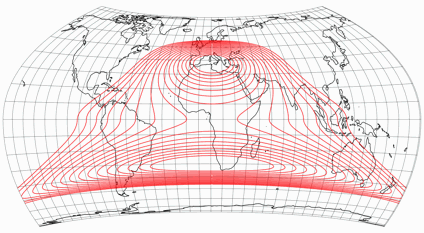
Im Laufe der Zeit gefiel mir diese Variante aber nicht mehr so gut. Erstens war sie mir ein bisschen zu breit, und zweitens habe ich etwas festgestellt: Während die Kartenbilder von Nord- und Südhalbkugel perfekt zusammengepasst haben, zeigen sich am Äquator Diskontinuitäten im Verlauf der Verzerrungen. Hier eine Darstellung der Isolinien der max. Winkelverzerrungen von 5 bis 20°:

Also fing ich wieder von vorne an. Diesmal wählte ich eine von Wagners originalen 1941er-Varianten^[3]^[4] für die nördliche Hemisphäre, oder in der Böhm-Notation: vii@61-65-60-0-205.128. Für die Südhalbkugel entschied ich mich, die gleiche Länge der Pollinie zu verwenden wie bei meiner ersten Variante, und die gleiche Krümmung der Breitenkreise wie in Wagners Original. Also musste ich nur noch herausfinden, welches Längenverhältnis von Äquator zu Zentralmeridian ich einzusetzen ist, damit die beiden Hemisphären exakt zu einander passen. Das läuft auf einen Entwurf mit der Böhm-Notation vii@37-65-60-0-225.76 hinaus.
Nun sind die Diskontinuitäten am Äquator verschwunden:

Vergleicht man die originale symmetrische Version mit meiner asymmetrischen, sieht man die Verbesserungen für den Süden deutlich:

Aber eine asymmetrische Projektion sollte vorteilhaft für beide Hemisphären sein. Vergleichen wir nun meine Variante mit einer anderen symmetrischen, bei der ich die Konfigurationsparamter für die Südhalbkugel auf die gesamte Karte angewandt habe:

Autsch.
Große Teile des Landes der nördlichen Hemisphäre kommen in dieser Konfiguration ebenfalls besser weg als in meinem asymmetrischen Experiment. In diesem Fall also könnte man frage: Wozu das Ganze? Nimm die symmetrische Abbildung mit der langen Pollinie, beide Hemisphären sind damit gut bedient! Vergiß den Kram mit der Asymmetrie!

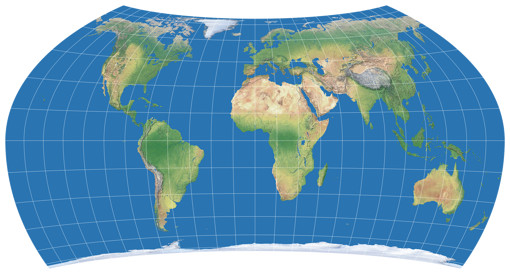
Mir gefällt die asymmetrische Projektion trotzdem besser, bei der anderen sieht die Ost-West-Streckung der nordpolaren Regionen in meinen Augen einfach grauenhaft aus. Vielleicht wird dies deutlicher, wenn man die beiden mal mit einem »echten« Kartenbild vergleicht:

In Bezug auf die Gesamtverzerrungswerte, ich muss es zugeben, ist die Variante mit den lang gestreckten Polen aber vermutlich besser. Andererseits hat Wagner wiederholt seine Meinung geäußert, dass man sich bei der Bewertung von Projektionen nicht allein auf Verzerrungswerte verlassen sollte. Ich bin ziemlich sicher, dass ihm die langen Pollinien nicht gefallen hätten. Und es ist natürlich absolut möglich, dass er auch meine asymmetrische Version abgelehnt hätte…

Quellenangaben

↑ Weia Reinboud: Cupola Projection and its Family (engl.)
Vorstellung der Cupola-Projektion auf Reinbouds Website.
↑ Weia Reinboud: The cupola projection – an asymmetric equal-area world map (engl.)
Die Abhandlung, in der die Cupola-Projektion vorgestellt wird (bezahlter Zugang)
↑ Wagner, Karlheinz:
Neue ökumenische Netzentwürfe für die kartographische Praxis.
In: E. Lehmann, ed., Jahrbuch der Kartographie 1941.
Leipzig: Bibliographisches Institut. 176–202.
↑ Wagner Bros.
Meine Vorstellung von Wagners eigenen vier Varianten des Wagner VII.