Fr, 5.1.2024 Die Winkel-Denner-Projektionen
Aktualisiert: Mo, 15.1.2024
Vor einiger Zeit habe ich erwähnt, dass es »noch etwas Gutes am Winkel-Snyder« gibt. Er ist nämlich sozusagen für die Schaffung von fünf sehr interessanten Projektionen von Peter Denner verantwortlich – und zwei weiteren von mir selbst.
Peter hat seine Projektionen im April vorgestellt, und zwar in einem Thread des mapthematics-Forums (engl.) Ich werde hier hauptsächlich das zitieren, was er dort gesagt hat; aber da ich auch die Verzerrungsdiagramme (abermals von Peter erstellt) zeige, mag es lohnend sein, diesen Blogpost zu lesen, auch wenn du diesen Thread schon gelesen haben solltest.
Bevor ich anfange, muss ich noch etwas sagen, was ich merkwürdigerweise noch nie erwähnt habe, obgleich es gut in die Grundwissen-Sektion meiner Website passen würde: Wir werden hier gleich über x- und y-Werte sprechen. Und ja, damit ist genau das gemeint, was Ihr (hoffentlich) noch aus Eurem Geometrie-Stunden in der Schule in Erinnerung habt. Denn genau ist es, worum es bei Kartenprojektionen geht: Umrechnung von sphärischen Koordinaten, so dass man sie in ein kartesisches Koordinatensystem einzeichnen kann.
Jetzt können wir loslegen – und, der Esel nennt sich immer zuerst, ich fange mit einer meiner eigenen Projektionen an.
Winkelähnliche Projektion I
In einem Kommentar im Februar erwähnte Peter Denner den Winkel-Snyder. Wir unterhielten uns dann weiter über die Projektion, und während dieser Unterhaltung fiel mir ein Experiment ein, welches ich um August 2018 durchgeführt hatte – und ich zeigte es Peter. Es war der Versuch einer »winkel-tripeligen« Projektion mit geringeren Flächenvergrößerungen (auf Kosten von höheren Winkelverzerrungen).
Die Idee war ganz einfach: Die x- und y-Werte des Winkel Tripel sind das arithmetische Mittel der Werte von der Rektangular- und der Aitoff-Projektion. Es ist also einleuchtend, dass man die Flächenvergrößerungen reduzieren kann, wenn man die Aitoff- durch die Hammer-Projektion ersetzt. Bei der Rektangularprojektion (auch als rechteckige Plattkarte bekannt) entschied ich mir für Schnittparallelen bei arccos(2/π) (≈50°28´, oder 50,46°, und somit ein Seitenverhältnis wie in Winkels Original) und 40° (Seitenverhältnis wie beim Winkel Tripel Bartholomew). Hier sind die Resultate – in beiden Fällen wurde der Hammer auf die Größe des Aitoff skaliert, bevor das Mittel gebildet wurde:
Vergleiche:
Winkelähnliche Projektion I (50,46°) vs. Winkel Tripel
Winkelähnliche Projektion I (40°) vs. Winkel Tripel Bartholomew
Winkelähnliche Projektion I (50,46°) vs. Winkelähnliche Projektion I (40°)
Ich war nicht besonders begeistert von dieser Projektion (und bin es immer noch nicht),
daher verwarf ich sie damals. Nun füge ich sie meiner Projektions-Kollektion
aus drei Gründen hinzu:
1. Sie ist zwar nicht großartig, aber sicher auch nicht schlecht;
2. der Hauptteil der Website dreht sich darum, Projektionen zu vergleich,
ihre Vor- und Nachteile aufzuzeigen, also haben auch nicht so
tolle Projektionen ihre Berechtigung;
3. sie eignet sich gut also Einleitung zu den Winkel-Denner-Projektionen.
Denn während ich nur sagte: »Ach, die sieht ja nicht so toll aus« und es dabei beließ, versuchte Peter herauszufinden, warum dies der Fall ist.
Winkel-Denner I
oder:
Winkel Tripel mit geringerer Flächenverzerrung
Also, als Peter sich gefragt hat, warum der Winkelähnliche I nicht so gut aussieht…
Ach was. Ich bin faul und werde ihn einfach aus dem o.g. Forums-Thread zitieren
(aber immerhin ins Deutsche übersetzt):
Ich fragte mich, woran dies liegen mag und dachte, der Grund ist vielleicht, weil auch die Abstände der Meridiane modifiziert werden, so dass alles nach außen in die Regionen mit starken Verzerrungen geschoben wird, wodurch besonders die Amerikas ziemlich gebogen aussehen.
Mir kam in den Sinn, dass man die Abstände der Breitenkreise des Winkel Tripel modifizieren könnte, ohne die Abstände der Meridiane zu verändern, wenn man Winkels Mittel der Rektangular- und der Aitoff-Projektionen für die x-Werte beibehält, aber das Mittel aus der Rektangular- und der (hochskalierten) Hammer-Projektion für die y-Werte verwendet.
Ich werde Peter in diesem Blogpost noch mehrfach zitieren, ohne dies jedesmal zu erwähnen. Sobald du einen Absatz siehst, der wie der vorhergehende aussieht, weißt du: Dies sind nicht meine eigenen Worte, sondern die von Peter. Und hier sind auch seine ersten Resultate, abermals mit den Schnittparallelen auf arccos(2/π) und 40° (noch etwas, was für den Rest des Blogposts beibehalten wird):
Vergleiche:
Winkel-Denner I (50,46°) vs. Winkel Tripel
Winkel-Denner I (40°) vs. Winkel Tripel Bartholomew
Winkel-Denner I (50,46°) vs. Winkel-Denner I (40°)
Wie der Winkelähnliche I hat der Winkel-Denner I geringere Flächenvergrößerungen auf Kosten höherer Winkelverformungen, aber Peter kam zu dem Schluss (und ich stimme ihm zu), dass seine Projektion insgesamt die bessere ist.
Winkel-Denner II
oder:
Winkel Tripel mit geringerer Winkelverzerrung
Augenscheinlich weckte dies Peters Experimentierfreude, und er fuhr fort:
Man kann die Breitenkreise des Winkel Tripel natürlich auch in die andere Richtung bewegen, so dass sie nahe des Äquators enger beieinander stehen, und nahe der Pole weiter voneinander entfernt. Auf den ersten Blick könnte man denken, dass es fir die y-Werte eine gute Wahl wäre, das Mittel der Plattkarte und der Aitoff-transformierten[1] stereographischen Projektion zu verwenden. Allerdings weichen die Abstände der Breitenkreise in der Stereographischen weitaus mehr von der Gleichabständigkeit ab als in der flächentreuen Azimutalprojektion, von welcher der Hammer-Entwurf abgeleitet ist. Dies läuft also auf eine viel stärkere Modifikation in den Abständen der Breitenkreise hinaus als in Projektion Nr. 1.
Also hat Peter Denner mal eben eine neue azimutale Projektion entwickelt, nahm den Durchschnitt der Rektangular- und der Aitoff-Projektion für die x- und den Durchschnitt der Rektangularprojektion und der Aitoff-transformierten Version dieser neu entwickelten Azimutalprojektion für die y-Werte, und presto! Wir haben den Winkel-Denner II, der im Vergleich zum originalen Winkel Tripel geringere Winkelverformungen auf Kosten von stärkeren Flächenvergrößerungen zeigt:
Vergleiche:
Winkel-Denner II (50,46°) vs. Winkel Tripel
Winkel-Denner II (40°) vs. Winkel Tripel Bartholomew
Winkel-Denner II (50,46°) vs. Winkel-Denner II (40°)
Bisher waren alle drei Projektionen dem originalen Winkel Tripel (natürlich absichtlich) sehr ähnlich. Die meisten Leute, mich selbst eingeschlossen, würden wahrscheinlich denken, es ist das Original, wenn man sie in einem Atlas oder auf einer Wandkarte gedruckt sähe. Die nächsten sehen etwas anders aus.
Winkel-Denner III
oder:
Winkel Tripel mit abgerundeten Ecken
Der eigentliche Grund, eine punktpolige Projektion mit der rechteckigen Plattkarte zu mitteln, ist die Einführung einer Pol-Linie. Wenn man allerdings akzeptiert hat, dass man für die x- und y-Werte nicht ein und dieselbe Eltern-Projektion verwenden muss, wird auch offensichtlich, dass man für die y-Werte eigentlich gar keine Mittelung mit der Rektangularprojektion vornehmen muss, um eine Pollinie zu erhalten. Nimmt man das Mittel der Rektangular- und der Aitoff-Projektion für die x-Werte und verwendet für die y-Werte nur den Aitoff, ganz ohne Mittelung, erhält man eine Projektion, die im Wesentlichen dem Winkel Tripel entspricht, allerdings mit abgerundeten Ecken:
Vergleiche:
Winkel-Denner III (50,46°) vs. Winkel Tripel
Winkel-Denner III (40°) vs. Winkel Tripel Bartholomew
Winkel-Denner III (50,46°) vs. Winkel-Denner III (40°)
Ich muss sagen, dass ich mir bei dem »im Wesentlichen dem Winkel Tripel entsprechen« sicher bin – obgleich sie im Zentrum der Karte tatsächlich fast identisch ist. Die äußere Form jedoch erinnert viel mehr an Winkels zweite Projektion; also könnte man diese Projektion vielleicht auch den »Lentikulären Winkel II« nennen. 😉
Winkel-Denner IV
oder:
Winkel Tripel mit abgerundeten Ecken und geringerer Flächenverzerrung
Der naheliegende nächste Schritt besteht nun darin, die Aitoff-Projektion durch die Hammer-Projektion und die [oben] vorgestellte Aitoff-transformierte neue azimutale Projektion zu ersetzen, wie in den Projektionen 1 bzw. 2, um die Abstände der Breitenkreise in dieser neuen Version des Winkel Tripels mit abgerundeten Ecken zu ändern. In den Projektionen 1 und 2 wird der Abstand der Parallelen jedoch durch die Mittelung mit der Rektangularprojektion gemildert. Nimmt man also nur die Hammer-Projektion oder die Aitoff-transformierte neue azimutale Projektion allein ohne Mittelung der y-Werte, dann weichen die Parallelen in der resultierenden Projektion stärker von der Gleichabständigkeit ab als in den Projektionen 1 und 2. Das heißt natürlich nicht, dass man das nicht machen kann, (…) aber ich persönlich mag in vermittelnden Projektionen keine Breitenkreise, die zu stark von den gleichen Abständen abweichen. (…) Anstatt also nur die Hammer-Projektion oder die Aitoff-transformierte neue azimutale Projektion ohne Mittelwertbildung für die y-Werte zu nehmen, nehmen wir zunächst den Mittelwert der Aitoff- und (hochskalierten) Hammer-Projektion für die y-Werte:
Vergleiche:
Winkel-Denner IV (50,46°) vs. Winkel Tripel
Winkel-Denner IV (40°) vs. Winkel Tripel Bartholomew
Winkel-Denner IV (50,46°) vs. Winkel-Denner IV (40°)
Und wir gehen direkt zur fünften Projektion über …
Winkel-Denner V
oder:
Winkel Tripel mit abgerundeten Ecken und geringerer Winkelverzerrung
… welche für die y-Werte den Mittelwert der Aitoff- und der neu entwickelten aitoff-transformierten azimutalen Projektion verwendet:
Vergleiche:
Winkel-Denner V (50,46°) vs. Winkel Tripel
Winkel-Denner V (40°) vs. Winkel Tripel Bartholomew
Winkel-Denner V (50,46°) vs. Winkel-Denner V (40°)
Die Projektionen IV und V haben signifikant niedrigere Gesamt-Winkelverformungen und in etwa die gleiche Gesamt-Flächenvergrößerung wie ihre Gegenstücke mit spitzen Ecken, Winkel-Denner I und II.
Das Resümee habe ich mir für später auf. Zunächst möchte ich noch auf eine weiteres meiner eigenen Experimente zu sprechen kommen.
Winkelähnliche Projektion II
Hinweis vom 15. Januar:
Die Winkelähnliche Projektion II wurde nach der ursprünglichen Vorstellung vom 5.1. noch einmal überarbeitet.
Wie oben gesagt, war ich nicht zufrieden mit der Winkelähnliche Projektion I,
aber ich wollte immer noch einen Winkel Tripel mit geringeren
Flächenvergrößerungen sehen (die Winkel-Denner-Projektionen existierten
zu diesem Zeitpunkt noch nicht).
Also habe ich es anders herum versucht: Anstatt den Aitoff durch eine Projektion
mit geringeren Flächenverzerrungen zu ersetzen, könnte ich doch die Rektangularprojektion
auswechseln!
Also habe ich den Aitoff mit der flächentreuen Zylinderprojektion gemittelt, aber
das sah mir nicht »winkelig« genug aus. Nun denn, dann nimm einfach eine Zylinderprojektion
die ein gewisses Maß an Flächenvergrößerungen zeigt, aber nicht so viel
wie die Plattkarte, und das wäre, ääähhmmm… Hoppla!
Erstaunlicherweise konnte ich keine einzige existierende Zylinderprojektion finden, auf die diese Beschreibung zutrifft.[2] Also entschied ich mich, den konfigurierbaren Wagner VII/VIII zu verwenden: Wenn man sowohl den begrenzenden Breitenkreis ψ1, als auch den Grenz-Meridian λ1 auf 0 (null) setzt, erhält man eine zylindrische Projektion (siehe dieses Beispiel in meinem Wagner-Variationen-Generator). Dann muss man nur noch eine Flächenvergrößerung in gewünschter Höhe hinzufügen. Ich entschied mich für eine 1,5-fache Vergrößerung bei 60° Nord/Süd, was in der Mitte der flächentreuen Zylinderprojektion und der rechteckigen Plattkarte liegt.
In der ersten Version der Winkelähnlichen II (veröffentlicht am 5.1.) habe ich
das gewünschte Seitenverhältnis (wie üblich beim flexiblen Wagner)
über die Variable p gesetzt und das Ergebnis ohne vorherige
Skalierung mit der Aitoff-Projektion gemischt.
Peter Denner hat dann eine etwas andere Version vorgeschlagen, welche
zwei Verbesserungen zeigt:
– Wie bei den o.g. Projektionen, wird eine Skalierung vorgenommen, wodurch
die Projektion aufgrund der gleichen Pol-Linien-Längen besser zum Rest der Serie passt,
– das Seitenverhältnis der zylindrischen Anteils wird durch die
Schnittparallele gesetzt, was die übliche Vorgehensweise bei
(Pseudo-) Zylindern ist und darüber hinaus erlaubt, den Winkelähnlichen II
mit exakt dem gleichen Seitenverhältnis wie die Winkel Tripel zu zeichnen.
Vergleiche:
Winkelähnliche Projektion II (50,46°) vs. Winkel Tripel
Winkelähnliche Projektion II (40°) vs. Winkel Tripel Bartholomew
Winkelähnliche Projektion II (50,46°) vs. Winkelähnliche Projektion II (40°)
Resümee
Wir haben uns sieben Alternativen zum Winkel Tripel angesehen.
Meine erste winkelähnliche Projektionen sowie
Winkel-Denner I & II sehen den Originalen von
Oswald Winkel und John Bartholomew sehr ähnlich – mit gewissen
Vorteilen, die jeweils durch gewisse Nachteile erkauft werden.
Winkel-Denner III, IV & V sind optisch eigenständiger
und mein zweiter winkelähnlicher Entwurf liegt irgendwo dazwischen.
Meiner Meinung nach sind diese drei Projektionen von Peter Denner
die interessantesten der hier gezeigten Reihe.
Die guten vermittelnden Eigenschaften des Originals bleiben erhalten,
die runden Ecken mögen für viele Augen angenehmer erscheinen
und verhindern eine Verwechslung mit dem Winkel Tripel.
Ich würde nicht soweit gehen zu behaupten, dass der Winkel Tripel im Übermaß verwendet wird.
Aber er kommt schon sehr häufig zum Einsatz, es kann also nicht schaden, auch mal
zu anderen Projektionen zu greifen. Winkel-Denner III, IV & V sind, in meinen Augen,
eine sehr gute Wahl für Atlanten, Wandkarten und viele Arten von thematischen Karten.
Meine persönlichen Favoriten sind Winkel-Denner I
(als Vertreter der »fast identisch zu Winkel Tripel«-Karten) und
Winkel-Denner IV (für die neuartigen Projektionen).
Verwendung der Projektionen
Kommen wir nun zu den schlechten Nachrichten: Abgesehen von den Skripten von d3-geo-projection gibt es derzeit keine Software, welche die hier aufgeführten Projektionen rendern kann (Ausnahme: der Winkelähnliche II, s.u.); und diese Skripte eignen sich hervorragend für Vektorgrafik-Karten und, wie man sieht, auch für webtaugliche Bilder – aber weniger für Grafiken, die gedruckt werden sollen.
Die guten Nachrichten, nun ja… die Formeln für die Projektionen sind nichts Ausgefallenes, sondern ganz einfache Mathematik. Es sollte nicht schwerfallen, sie in Kartenprojektions-Programme einzubauen. Was natürlich nicht notwendigerweise bedeutet, dass dies auch passieren wird. 😕
Sechs der obigen Projektionen verwenden eine Skalierung vor der Mittelung der Werte – dieser
Vorgang wird von dem Programm
Geocart
leider nicht unterstützt. Ausnahme ist die Winkelähnliche Projektion II,
bei welcher man die Skalierung mittels der Projektionsparameter direkt vornehmen kann.
In Geocart kann man also zunächst eine Karte mit der Aitoff-Projektion erzeugen,
dann eine im »generalized Wagner«, den man für die Version 50,46°
mit folgenden Parametern füttert:
a = 2001.949, b = 1571.3114, m = 0.001131, m2 = 0.69016, n = 0.000318
Für 40° verwendet man:
a = 2408.9448, b = 1571.3114, m = 0.001131, m2 = 0.69016, n = 0.000318.
Danach selektiere beide Karten, rufe das Menü Map → New Blended auf
und mische sie mit P = 0.5.
Um die sieben Projektionen mit d3 zu rendern, lade die folgende
Datei runter – aber bitte beachte, dass es sich hierbei nicht
um eine unabhängige, gebrauchsfertige Datei handelt!
Du wirst sie in deine d3-Umgebung einsetzen müssen. Die Datei
ist nur hilfreich, wenn du mit d3 arbeitest (oder vorhast, es zu tun),
oder z.B. wenn du die Projektion in eine andere Software übernehmen willst:
d3-geo-projection-code-for-winkeldenner.js.zip
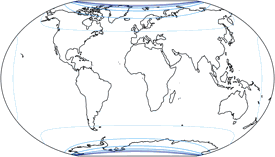
Verzerrungen
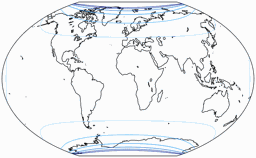
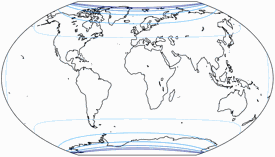
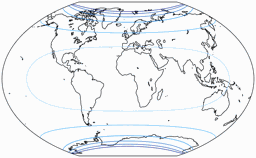
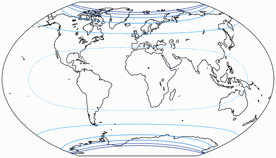
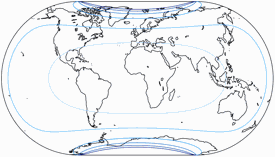
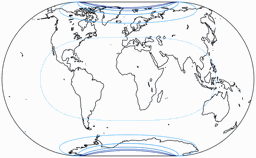
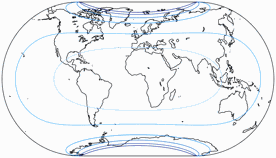
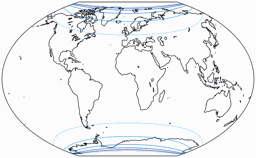
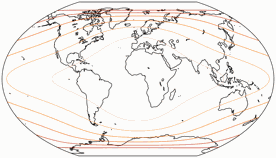
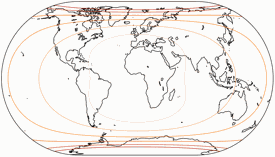
Regelmäßiger Besucher meines Blogs werden wissen: Wenn Peter Denner involviert ist, sind Verzerrungsgrafiken nicht weit! 😉 Hier sind sie also – für alle sieben Projektionen, jeweils mit den Schnittparallelen (im Rektangularprojektion-Anteil) auf at 50,46° und 40°.
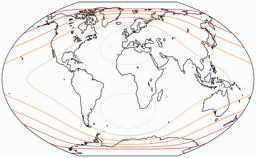
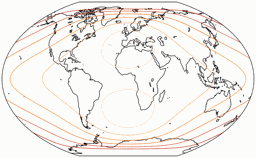
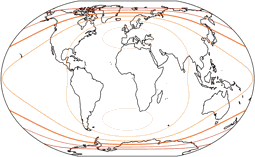
Flächenvergrößerungen
Die Linien werden gezeigt für eine Flächenvergrößerung (in Bezug auf den Wert in der Kartenmitte) von:
1,2; 1,5; 2,0; 2,5; 3,0; und 3,5.
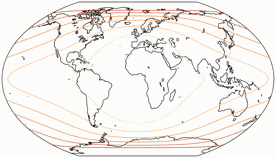
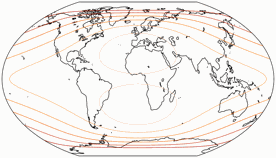
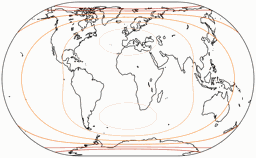
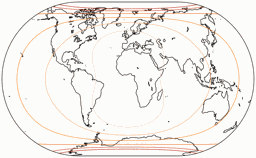
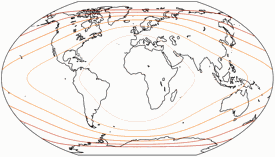
Winkelverformungen
Die Isolinien werden gezeigt für eine maximale Winkelverzerrung von:
10°, 20°, 30°, 40°, 50°, und 60°.
Vergleichsmatrix
Anhand der folgenden Tabellen kannst du die unterschiedlichen Variante direkt miteinander vergleichen.
Seitenverhältnis des originalen Winkel Tripel
Seitenverhältnis des Winkel Tripel Bartholomew
Nebenprodukte
Der Quellcode enthält einigen Nebenprodukte: Es gibt eine Funktion für die Rektangularprojektion mit Schnittparallele (die es erstaunlicherweise in d3 zuvor nicht gab), Peter Denners neue Azimutalprojektion – und eine, die ich Wagner 0[3] nenne: Wie oben beschrieben, wurde der Winkelähnliche II mit Hilfe des generalisierten Wagner VII entwickelt, aber es kam mir ein wenig ungünstig vor, eine lentikuläre Projektion zu verwenden, die dann zur zylindrischen gepresst wird. Also ist der Wagner 0 von vornherein zylindrisch, aber man kann immer noch ein Kontinuum an Projektionen mit jedem gewünschten Ausmaß an Flächenvergrößerung erzeugen, welches zwischen den beiden Extrema, der flächentreuen Zylinder- und der Rektangularprojektion, liegt. Der Wagner 0 lässt sich mit einer reduzierten Variante der Böhm-Notation beschreiben, z.B. hat Wagner 0 75-180 eine 1,75-fache Flächenvergrößerung bei 60° Nord/Süd und ein Seitenverhältnis von 1:1,8.[4]
Quellenangaben / Fußnoten
- ↑ Aitoff-transformiert: Unter Verwendung jener Transformation, die Aitoff auf die flächentreue Azimutalprojektion angewandt hat, d.h. Umbeziffern nur in x-Richtung bei einem Grenzmeridian von 90°.
- ↑ Tatsächlich gibt es eine Projektion, die meinen Wünschen entspricht: Pavlovs zylindrischer Entwurf – der sogar ein sehr ähnliches Ausmaß an Flächenvergrößerung aufweist (1,6 bei 60° N/S). Aber irgendwie habe ich ihn immer übersehen. 😳
-
↑
Wagner 0 = Wagner Null, nicht Ooh wie Organa.
Wagner I bis IX sind in der Reihenfolge nummeriert, in der Wagner sie in seinem 1949er Fachbuch »Kartographische Netzentwürfe« aufgeführt hat. Auf den Seiten davor jedoch benutzt der die flächentreue Zylinderprojektion als Beispiel, um den Vorgang des Umbezifferns zu demonstrieren. Augenscheinlich hielt er das Resultat aber nicht für einen gebrauchstüchtigen Kartennetzentwurf, also zeigte er nur die neun bekannten, von dem Sinusoidal-, dem Mollweide- und azimutalen Entwürfen abgeleiteten, Projektionen. Daher habe ich gleich zwei Gründe, die hier gezeigte Projektion Wagner 0 zu nennen: Ihre Stellung im Buch und der Wert, der ihr von ihrem Urheber zugemessen wurde. - ↑ Mehr Informationen über Wagners Transformationsmethode, »das Umbeziffern« und die Böhm-Notation gibt es im Artikel Das Umbeziffern oder kürzer in diesem Blogpost oder in den Hinweisen beim Wagner-Variationen-Generator (WVG-7) oder .

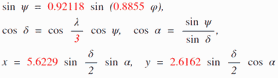




















 Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Kommentare
Sei der erste, der einen Kommentar hinterlässt!