Adams, Baranyi, Winkel-Snyder

Fr, 16.6.2023 Adams, Baranyi, Winkel-Snyder

Nach fünf Monaten gibt es auch endlich mal wieder Neueinträge in meiner Projektions-Kollektion. Und passenderweise sind es dann auch direkt fünf. 🙂

Eine weitere konforme Projektion von Adams

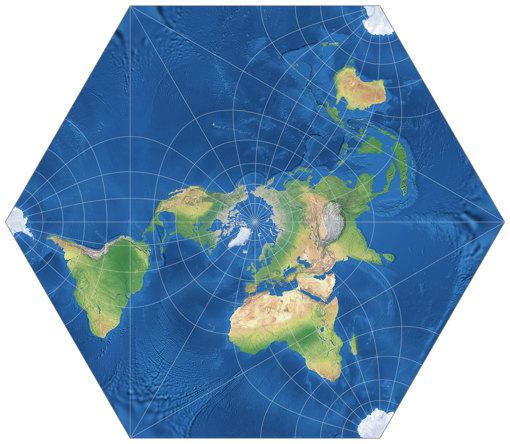
Vor drei Jahren habe ich Adams’ Erde in einem Sechseck mit einem ungewöhnlichen Kartenzentrum in meinem Projektionskalender gezeigt. Vor ein paar Wochen habe ich eine Nachricht erhalten, in der ich gebeten wurde, diesen Entwurf in meine Projektions-Kollektion aufzunehmen, vorzugsweise in der von Adams vorgeschlagenen polständigen Lage.

Hää?
Hab ich das nicht schon längst getan?
Nein, hatte ich nicht. Dies sei hiermit nachgeholt. Danke, Henry, dass du mich darauf aufmerksam gemacht hast! 🙏

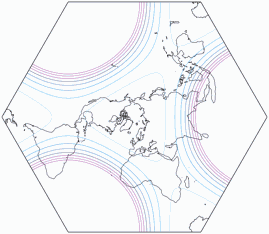
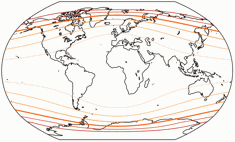
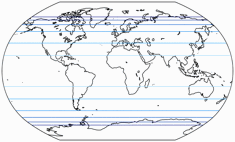
Hier noch die Darstellung der Flächenvergrößerung, gezeigt im Verhältnis zum Wert in der Mitte der Karte. Die Linien repräsentieren eine Vergrößerung um den Faktor
1,2; 1,5; 2,0; 2,5; 3,0; 3,5; 4,0; 4,5; und 5,0:

Drei bisher fehlende Projektionen von Baranyi

Letztes Jahr habe ich vier Projektionen von János Baranyi zu meiner Kollektion hinzugefügt und erwähnt, dass es noch drei weitere gäbe, von denen ich leider keine Grafiken erzeugen kann. Nun, ratet mal – jetzt kann ich es! Hier sind Baranyi V, VI und VII:

Du kannst alles, was ich über sie zu sagen habe, in dem oben verlinkten Blogpost nachlesen (was soll’s, hier ist der Link nochmal), also gibt es keinen Grund, hier großartig herumzuschwätzen; und ich kann direkt auf den wichtigen Punkt kommen:

Ich kann Visualisierungen der Verzerrungen von allen sieben Baranyi-Projektionen präsentieren! Und ich kann Euch sagen, das war vielleicht eine Arbeit, denn… *räusper* Okay, vermutlich war es viel Arbeit, aber nicht für mich, denn mal wieder hat Peter Denner sie generiert und mir zur Verfügung gestellt. Vielleicht sollte ich in Blogposts demnächst lieber darauf hinweisen, wenn ich Peter ausnahmsweise mal keinen Dank schulde? 😉

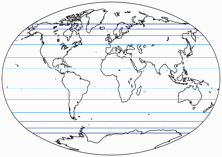
Zunächst die Winkelverzerrungen, die Isolinien werden gezeigt für eine max. Verzerrung von:
10°, 20°, 30°, 40°, 50°, und 60°.

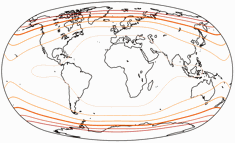
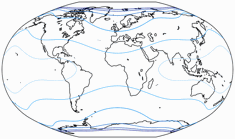
Bei der Flächenvergrößerung, gezeigt im Verhältnis zur geringsten Verzerrung, repräsentieren die Linien Werte von:
1,2; 1,5; 2,0; 2,5; 3,0; und 3,5.
Der geringste Wert tritt normalerweise in der Kartenmitte auf, aber bei Baranyi III bis VII dort, wo der Äquator auf den Rand der Karte trifft.

Ein ziemlich nützlicher Fehler von Snyder

In einem Artikel von 1977 listete John P. Snyder den Winkel II fälschlicherweise als arithmetisches Mittel der Rektangular- und der Mollweide-Projektion auf (Apian II anstatt Mollweide wäre richtig). Später korrigierte er diesen Fehler, und Evenden listete die Rektangular/Mollweide-Variante als Winkel-Snyder.^[1]^[2]

Und warum war dies ein nützlicher Fehler?
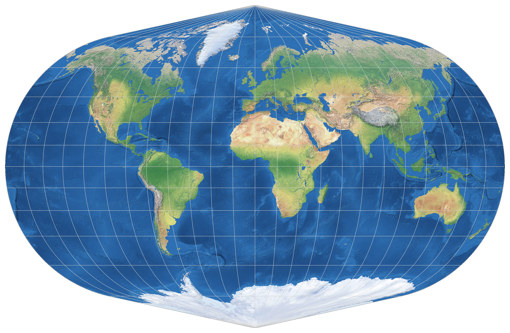
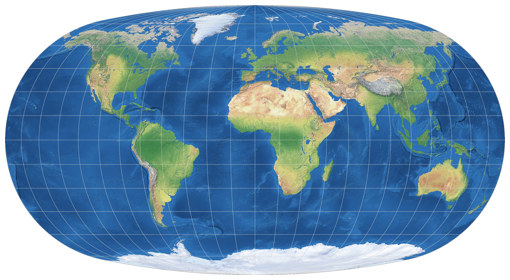
Weil der Winkel-Snyder eine sehr gute pseudozylindrische vermittelnde Projektion ist! Mir gefällt er sogar besser als der Winkel II. Aber urteile selbst: Winkel II vs. Winkel-Snyder.
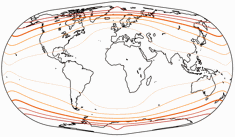
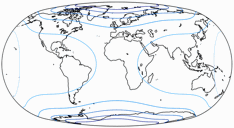
Die Verteiling der Verzerrungen ist sicher nicht spektakulär, aber durchaus gelungen:

Ich habe schon zuvor darüber gesprochen:^[3] Oswald Winkel verwendete bei der Mittelwertbildung aller drei Projektionen eine Schnittparallele von arccos(2/π) – oder gerundet 50°28´ – in der Rektangularprojektion. Aber natürlich kann man hier einen anderen Wert wählen, wie das ja schon am Beispiel des Winkel Tripel gezeigt wurde, mit einem Wert von 40° beim Winkel Tripel Bartholomew oder 0°, also dem Äquator, beim Winkel Tripel BOPC. Hier zwei Beispiele – einerseits übertragen Bartholomews 40° auf den Winkel-Snyder; andererseits verwenden wir 28°, die (zumindest annähernd) von Evenden in einer Illustration gezeigt wurden:

Ich denke, ich werde einen davon, oder vielleicht auch beide, demnächst meiner Projektions-Kollektion hinzufügen.
Es gibt aber noch etwas Gutes am Winkel-Snyder: Obwohl ich den ihn schon eine Weile kannte, wurde ich in der englischen Version dieses Blogs durch einen Kommentar im Februar erneut darauf aufmerksam gemacht, und in der Folge… ach, darüber werde ich bald sprechen. Und vielleicht weißt du es ja auch schon.
Bis die Tage!

Quellenangaben / Fußnoten

↑ Snyder, John P.: Flattening the Earth: Two Thousand Years of Map Projections.
Chicago 1993, Seite 307.
↑ Evenden, Gerald I.: libproj4-Handbuch
Falmouth 2008, Seite 66.
↑ Siehe meinen Blogpost Happy Birthday, Winkel Tripel! aus dem März 2021.

Permalink