Do, 18.3.2021 Happy Birthday, Winkel Tripel!
Vor hundert Jahren, im Jahre 1921, stellte Oswald Winkel
seine »Tripelprojektion« – heutzutage meist Winkel Tripel genannt,
manchmal auch Winkel III oder einfach der Winkelsche Entwurf –
der Öffentlichkeit vor.[1]
Herzlichen Glückwunsch!
Der Artikel erschien in der Dezember-Ausgabe von Petermanns Mitteilungen, also wären die Glückwünsche vielleicht später im Jahr angemessen. Andererseits ist die Original-Zeichnung unterschrieben mit: Erstmalig entworfen am 15. September 1920. Also ist das der eigentliche Geburtstag…
Der Winkel Tripel war damals, als ich nur eine Handvoll von Entwürfen kannte (nämlich, außer dem Jubilar, Mollweide, van der Grinten I, Gall-Peters und natürlich die Mercator-Projektion) meine Lieblingsprojektion. Nun, mittlerweile kenne ich ein paar Projektionen mehr 😉 und es gibt andere, die ich vorziehe, aber der Winkel Tripel gefällt mir immer noch verdammt gut. Wichtiger aber ist, dass es sich um eine absolute bemerkenswerte Projektion handelt.
Bevor wir aber auf das Bemerkenswerte eingehen, möchte ich ein paar Worte wiederholen, die ich schon an anderer Stelle gesagt habe:
Oswald Winkel hat den Winkel Tripel entworfen, indem er das arithmetische Mittel aus
der rechteckigen Plattkarte und der Aitoff-Projektion errechnete.
Nun kann man aber bei der Plattkarte sog. Schnittparallelen setzen, welche sich auf
das Gesamtbild der Karte auswirken. Winkel entschied sich für annähernd 50°28´ – arccos(2/π)
für die Mathematiker unter uns[2] –,
bevor er diese Variante der Plattkarte mit dem Aitoff mixte.

Die Aitoff-Projektion…
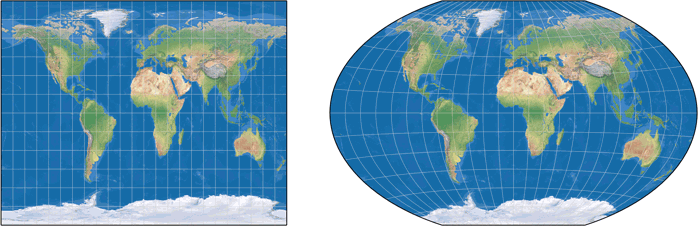
… gemittelt mit der rechteckigen Plattkarte, Schnittparallelen auf ca. 50°28´,
ergibt den originalen Winkel Tripel.
Um 1955 entwarf John Bartholomew für die Verwendung im Times Atlas eine Variante des Winkel Tripel,
bei welcher er für den Plattkarten-Anteil die Schnittparallelen auf 40° setze. Dies resultiert in einer breiteren
Darstellung der Erde als das Original und – so argumentieren viele Leute (u.a. auch ich) – in einer besseren
Verteilung der Verzerrungen. Übrigens hat auch Karlheinz Wagner schon 1949 darauf hingewiesen,
dass dieser Wert »für eine Erdkarte wohl als das Günstigste anzusehen ist« und
zeigte eine entsprechende Grafik.[3]
Diese Variante wird hier auf der Website als »Winkel Tripel Bartholomew« gelistet.
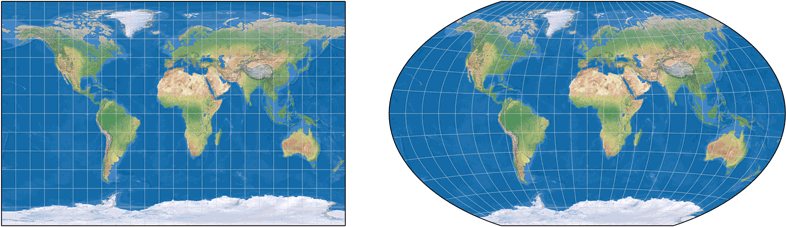
Setzt man die Schnittparallelen des Plattkarten-Anteils auf 40°, ergibt sich der Winkel Tripel Bartholomew,
den wir uns auch noch einmal in einer Großdarstellung ansehen:
Der Winkel Tripel wurde vergleichsweise schnell extrem populär – zumindest im deutschsprachigen Raum. 1941 bemerkte Wagner, dass man ihn »in verschiedensten neuen Kartenwerken fast aller maßgeblichen Firmen« sieht und lobte »seine verblüffende Formen- und Lagetreue. Man könnte meinen, Winkel habe behutsam die zweifach gekrümmte Kugeloberfläche geglättet, immer bedacht, die einzelnen Teile nicht gewaltsam in eine bestimmte Richtung zu zwingen, sondern nach allen Seiten ein wenig nachgebend, um schließlich ein in jeder Hinsicht möglichst ähnliches Abbild zu bekommen«.[4]
Nebenbei bemerkt, wurde der Wagner VII von seinem Schöpfer explizit als flächentreue Alternative zum vermittelnden Winkel Tripel vorgestellt. Ohne Winkels Entwurf hätte es den von mir sehr geschätzten Wagner VII also möglicherweise nie gegeben…
Natürlich gab es nicht nur Lob. Sogar Wagner, der den Entwurf meistens mit
so netten Worten wie den oben zitierten bedenkt, schmuggelte eine vorsichtige Kritik ein:
»Die Zunahme der Flächenvergrößerung vom Äquator bis zum Pol ist aber doch recht beträchtlich«.[5]
Max Eckert hingegen beginnt mit halbherzigen freundlichen Worten, um dann die aphylaktische Natur
des Winkel Tripel zu kritisieren:[6]
Um meine Meinung über die Winkelsche Projektion gefragt, muß ich sagen, daß sie mir gleichfallls recht gut gefällt, und ich sie für allgemeine Übersichtkarten recht geeignet halte. Ich selbst, getragen von einem gesunden geographischen und mathematischen Bewußtsein, ziehe indessen die Projektionen vor, die ein sicheres mathematisches Rückgrat haben und entweder flächen- oder winkel- oder längentreu (mittabstandstreu) sind (…)
Herbert Hufnagel weist auf die unvorteilhafte Verteilung der Verzerrungen hin:[7]
Die Fläche nimmt vom Äquator zu den Polen stetig zu (…) doch ändert sich die Fläche auch mit zunehmendem Abstand vom Mittelmeridian. Die Zunahme vom Äquator zu den Polen hin ist aber je nach Abstand des Meridians von der Mitte verschieden stark. Das führt dazu, daß auf dem Äquator von der Kartenmitte nach außen die Fläche zunimmt, auf den Breitenkreisen jenseits etwa des 50. Breitengrades aber abnimmt. Diese Erscheinung ist das Ergebnis aus der Mischung zwei Entwürfe mit sehr unterschiedlichen Eigenschaften; sie macht bei Vergleichen eine Berücksichtigung der Flächenzunahme unmöglich.
… und schließt, dass Entwürfe mit »kontrollierter Flächenverzerrung« nach Art des Wagner VIII
vorzuziehen sind.
Hey! Das macht meine eigenen Wagner BCW-A und
F13 Copycat zu empfehlenswerten Alternativen zum Winkel Tripel! Ich liebe diese Kritik!
😁😉
Okay, Spaß beiseite:
Abgesehen von der Verwendung im Times Atlas blieb der Winkel Tripel
außerhalb des deutschsprachigen Raums »nahezu unbekannt« – zumindest
laut Hufnagel.[8] Dies änderte sich 1998, als die National Geographic Society die
Originalversion als Standard-Projektion für Weltkarten übernahm.
Und heutzutage ist er, soweit ich das beurteilen kann, weltweit eine der am häufigsten benutzten Projektionen.
Und nun, zu dem bemerkenswerten Teil…
Zunächst einmal war der Winkel Tripel die erste Projektion mit Pol-Linie aus jener Gruppe, für die ich die Bezeichnung lentikulär[9] übernommen habe (während andere Namen wie polykonisch, pseudoazimutal usw. bevorzugen) – aber das ist nicht das eigentlich Bemerkenswerte.
Ich habe schon mehrfach darauf hingewiesen, dass ich nicht gut in Mathe bin.
Vielleicht verstehe ich also einiges falsch, aber –
zwei Projektionen zu mischen, erscheint mir ziemlich trivial, wenn
ich mir die Formeln von neueren Projektionen von z.B.
Canters oder Györffy ansehe.
Und doch …
- Der Winkel Tripel Bartholomew nahm den Spitzenplatz ein in Canters’ Liste von 23 bekannten Projektionen, sortiert nach dem »mean finite scale factor« K1; [10] (die originale Version fand leider keine Erwähnung)
- Die Plätze 1 (Original) und 2 (Bartholomew) unter den von Goldberg & Gott (2007) aufgeführten sechs »Projektionen mit dem niedrigsten Wert von ∑ε«; [11]
- die gleichen Plätze in Frančulas (1971) Liste von 10 oft benutzten Entwürfen, sortiert nach dem Airy-Kavraiskiy-Kriterium EAK; [12]
- Platz 2 für die Bartholomew-Variante in Györffys Liste mit dem verwandten EK-Wert von 18 bekannten Projektionen (abermals wird das Original nicht aufgelistet); [13]
-
und Platz 9 (Bartholomew) und 12 (Original) in einer Liste von 100 Projektionen,
sortiert nach Richard Capeks Verzerrungswert Q [14]…
Huch, was ist hier passiert? Nun, abgesehen davon, dass ich die Brauchbarkeit von Q mittlerweile etwas anzweifle (was sehr ärgerlich ist, immerhin ist es die umfangreichste Studie), erreichen sie 81,3 bzw. 80,7 Punkte, was trotz ihrer scheinbar »schlechten« Platzierung immer noch ein sehr guter Wert ist.
Natürlich, die Untersuchungen von Canters, Goldberg & Gott, Frančula und Györffy
waren nicht gerade umfangreich.
Zum Beispiel haben sie alle nicht den
Ginzburg VI (1950) oder den
Ginzburg IX (1966)
untersucht, und ich habe gerade vor ein paar Tagen erfahren, dass diese beiden nach dem
Airy-Kavraiskiy-Kriterium und dem Messverfahren von Goldberg-Gott den Winkel Tripel schlagen.
Selbst unter meinen eigenen Experimenten befinden sich zwei – der
F13 Copycat
und der
Wagner vii@65-76-60-40-168
–, die an unserem Jubilar vorbeigezogen sind.[15]
Es ist also durchaus möglich, dass es noch weitere
Projektionen gibt, die den Winkel Tripel überrunden. Aber ich denke, es kann keinen
Zweifel geben, dass ihm eine sehr vorteilhafte Balance von Winkel- und Flächenverzerrungen
gelingt.
Es gibt auch keinen Zweifel daran, dass der Winkel Tripel mehrfach überrundet wurde,
seitdem das Zeitalter des computer-unterstützen Designs von Kartenprojektionen
angebrochen ist:
Und zwar von Entwürfen von Frančula, Canters,
Györffy, wahrscheinlich auch Kunimune[16]…
Aber die Sache bei diesen ist: Sie alle haben Computer genutzt, um Projektionen zu optimieren.
Sie haben etliche Konfigurationen durchgerechnet, bis sie bei möglichst günstigen
Verzerrungswerten gelandet sind.
Ihre Projektionen wurden mit einem beachtlichen Berechnungsaufwand erzeugt.
Benötigt man also Rechenpower, um den Winkel Tripel zu schlagen? – Nein.
Aber die meisten Projektionen, die besser sind,
wurden durch Optimierungsprozesse geschaffen.
Man kann also sagen: Es ist nicht unmöglich, den Winkel Tripel zu schlagen
– aber einfach ist es sicher nicht.
Und dass man dies über eine Projektion sagen kann, die einfach aus dem arithmetischen Mittel zwei anderer Projektionen geschaffen wurde – das ist in meinen Augen tatsächlich bemerkenswert.
Hinweis: Wenn ich davon rede, dass eine Projektion »besser« ist als die andere oder »sie schlägt«, dann solltest Du in Deinem Kopf stets hinzufügen: »gemäß einer bestimmtem Anwendung eines bestimmtem Vergleichsschemas«. Es gibt keine endgültige Lösung, um die Gesamtverzerrung verschiedener Projektionen zu vergleichen. Gibt es wenigstens eine Standard-Lösung? – Nein. Der Stand der Dinge ist ziemlich genau so, wie der in dem herrlichen xkcd »Standards«-Cartoon dargestellt wird.
… und Herzlichen Glückwunsch, Winkel I und II!
Auch bei Winkel I und II handelt es sich um Mischkarten. Die erste Eltern-Projektion ist,
wie beim Tripel, die rechteckige Plattkarte mit Schnittparallelen auf arccos(2/π),
die zweite ist beim Winkel I
die Sinusoidal-Projektion
und beim Winkel II der
Apian II.
Sie wurden früher entworfen, nämlich 1914 und 1918, der Öffentlichkeit aber aber meines Wissens im gleichen
Artikel präsentiert, der auch den Winkel Tripel vorstellte.
Sie sind weitaus weniger berühmt als der Winkel Tripel, obwohl der Winkel II in meinen Augen eine sehr gelungene, verwendbare Projektion mit geraden, gleichabständigen Breitenkreisen ist – und wie mir kürzlich erklärt wurde, ist er unter den Pseudozylindern ebenso schwer zu schlagen wie sein lentikulärer Bruder.
Und der Winkel I, nun…
Wie ich schon einmal gesagt habe, scheinen Projektionen
mit sinusförmigen Meridianen nicht besonders beliebt zu sein.
Ich selbst finde ihn nicht einmal unattraktiv, andererseits
wüsste ich aber auch keinen Anwendungszweck, bei dem er
meine erste Wahl wäre.
Wie auch immer: Herzlichen Glückwunsch auch an Winkel I und II!
Quellenangaben / Fußnoten
-
↑
Winkel, Oswald: Neue Gradnetzkombinationen. In: Petermanns Mitteilungen. 67, 1921, 248–252.
English translation (with figures) available atcsiss.org/map-projections/microcam/newgrat.pdf
Scan of the original German article (no figures, poor quality) atcsiss.org/map-projections/microcam/winkel.pdf
Update May 5th, 2022: Sorry, the links above don’t work anymore. 😕 -
↑
arccos(2/π) ergeben nicht genau 50°28´, sondern – sofern ich da keinen Rechenfehler gemacht habe –
50,45977625219° oder 50°27´35,1945″. Diese Differenz kann man in fast allen Fällen aber tatsächlich vernachlässigen:
Auf einer gedruckten Karte sind die Unterschiede wahrscheinlich geringer als Ungenauigkeiten, die durch den Verzug
des Papiers, auf dem die Karte gedruckt ist, entstehen.
Und bei einer rein digitalen Karte kommt bei einer Breite von ca. 12.000 Pixeln zu einer maximalen Differenz von zwei Pixeln. (Und ja, das habe ich ausprobiert…) -
↑
Wagner, Karlheinz:
Kartographische Netzentwürfe.
Leipzig 1949, Seite 225 -
↑
Wagner, Karlheinz:
Neue ökumenische Netzentwürfe für die kartographische Praxis.
In: E. Lehmann, ed., Jahrbuch der Kartographie 1941.
Leipzig: Bibliographisches Institut. 176–202. - ↑ Wagner 1949:226
-
↑
Eckert-Greifendorf, Max:
Kartographie. Ihre Aufgaben und Bedeutung für die Kultur und Gegenwart
Berlin 1939, Seite 75f. -
↑
Hufnagel, Herbert:
Die Verwendung von Kartennetzen.
In: Kartographisches Taschenbuch 1988/89.
Bonn 1988. 11–20. -
↑
Hufnagel, Herbert:
Ein System unecht-zylindrischer Kartennetze für Erdkarten.
In: Kartographische Nachrichten 39/3: 89-96; München Juni 1989. - ↑ siehe Strebe, Daniel “daan”: Map Projection Essentials
-
↑
Frank Canters:
Small-scale Map Projection Design.
London & New York 2002. -
↑
Goldberg & Gott, 2007:
Flexion and Skewness in Map Projections of the Earth
physics.drexel.edu/~goldberg/projections/goldberg_gott.pdf - ↑ Nedjeljko Frančula, 1971: Die vorteilhaftesten Abbildungen in der Atlaskartographie
-
↑
János Györffy, 2018: Minimum distortion pointed-polar projections for world maps by applying graticule transformation
doi.org/10.1080/23729333.2018.1455263 -
↑
Richard Capek, 2001:
Which is the Best Projection for the World Map?
icaci.org/files/documents/ICC_proceedings/ICC2001/icc2001/file/f24014.pdf - ↑ Der F13 Copycat wurde im Blogpost Die Frančula-Projektionen vorgestellt, der Wagner vii@65-76-60-40-168 in Zwei neue Projektionen, drei Varianten, einige Korrekturen.
- ↑ Justin Kunimume 2019: Introducing the Danseiji Projections
P.S.: Und Herzlichen Glückwunsch auch an Dich, K.J.! 😁




 Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Kommentare
Sei der erste, der einen Kommentar hinterlässt!