Zwei neue Projektionen, drei Varianten, einige Korrekturen

Mi, 1.1.2020 Zwei neue Projektionen, drei Varianten, einige Korrekturen

Zum Beginn des Jahres 2020 möchte ich schnell ein kleines Update veröffentlichen.
Hier sind also zwei neue Projektionen, drei neue Varianten – und ein paar mehr oder weniger wichtige Korrekturen.

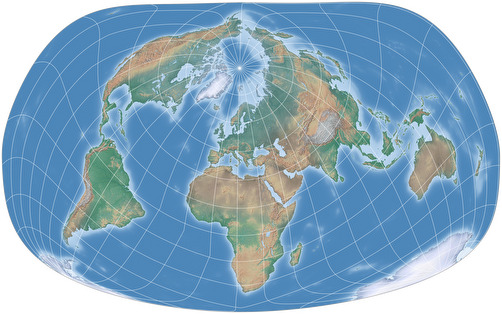
Die Bertin-Rivière-Projektion

Basierend auf einer Zeichnung von Jacques Bertin aus dem Jahre 1953, für die keine mathematische Formel existiert, entwickelte Philippe Rivière 2017^[1] diese neue Projektion
. … Nun, ich nenne es eine neue Projektion, denn in meinen Augen weicht sie zu weit vom Original ab, um sie eine Approximation zu nennen oder unter dem Namen Bertin-Projektion zu veröffentlichen. Also habe ich mich für den Namen entschieden, unter dem sie auch in der Software G.Projector gelistet ist:
Bertin-Rivière.

Mathematisch wurde die erzeugt aus der Briesemeister-Projektion^[2], die ihrerseits von der Hammer-Projektion abgeleitet wurde – also, hey, vielleicht sollte ich sie die Hammer-Briesemeister-Bertin-Rivière-Projektion nennen? 😉 Neee, lieber nicht.

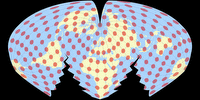
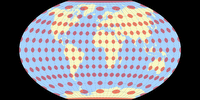
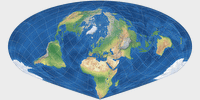
Wie auch immer, es ist eine interessante Projektion, welche die Verzerrungen der Landmassen gering hält. Hier ist sie:

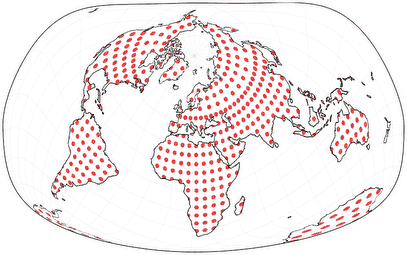
Und um die spezifische Verteilung der Verzerrungen zu betonen, folgt hier eine Darstellung, bei der die tissotsche Indikatrix auf die Landmassen begrenzt ist:

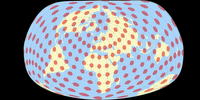
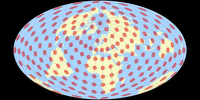
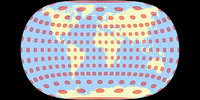
Und hier ist die übliche Darstellung der tissotschen Indikatrix, zusammen mit der »mathematischen Mutter-Projektion« Briesemeister; sowie der auch nicht ganz unähnlichen Sinu-Mollweide in unterbrochener und un-unterbrochener Form.

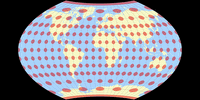
Bertin-Rivière vs. Briesemeister
Bertin-Rivière vs. Sinu-Mollweide
Bertin-Rivière vs. Sinu-Mollweide (nicht unterbrochen)

Györffy E

2018 stellte János Györffy eine Serie von fünf Minumum-Error-Projektionen vor^[3], die er mit den Buchstaben A, B, D, E und F benannte (C wurde verworfen, da sich keine bemerkenswerten Unterschiede zur Variante B zeigten).^[4] Sein Ziel war es, in aphylaktischen (vermittelnden) Projektionen mit punktförmigen Polen sowohl Flächen-, als auch Winkelverzerrungen zu minimieren und dabei eine äußere Form der Projektionen zu erreichen, die »den Betrachter an den Globus erinnern«.
Bei A und B handelt es sich um pseudozylindrische Projektionen, während D, E und F in die Klasse der lentikulären Entwürfe gehören.

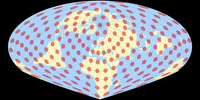
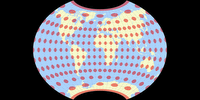
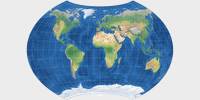
Aus dieser Serie kann ich derzeit leider nur die vierte Variante, den Györffy E, präsentieren:

Vergleichen wir die Tissotsche Indikatrix dieser Projektion mit einigen ähnlichen Projektionen… Upps! Die gibt es gar nicht!
Abgesehen vom Aitoff (der wirklich nicht ähnlich aussieht), gibt es keine lentikulären vermittelnden Projektionen mit punktförmigen Polen! Machen wir also das zweitbeste, vergleichen wir sie mit lentikulären vermittelnden Projektionen mit Pol-Linie – davon gibt es so einige, also habe ich ein paar herausgepickt, deren Flächenvergrößerungen so ungefähr denen des Györffy E entsprechen. So ganz ungefähr.

Mit den folgenden Links kannst Du den Györffy E auch direkt mit den sechs Projektionen vergleichen…
(Hinweis: Die Links schalten den Experten-Modus des Vergleichs ein. Für diese Paarungen empfiehlt es sich, bis zu den »auf gleiche Breite skalierten« Beispielen runter zu scrollen.

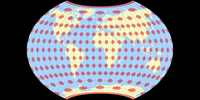
Györffy E vs. Kramer VII
Györffy E vs. Winkel Tripel
Györffy E vs. Ginzburg V
Györffy E vs. Wagner IX.i
Györffy E vs. Wagner IX, Canters Optimierung
Györffy E vs. Wagner vii@65-76-60-40-168

Drei neue Varianten

Darüber hinaus habe ich drei Varianten von Projektionen, die es hier schon länger zu sehen gab, hinzugefügt…

Die Rektangularprojektion ist schon in zwei Varianten gelistet, mit dem Äquator als Schnittparallele (= Quadratische Plattkarte oder Plate carrée) und mit Schnittparallelen auf 35,6° Nord/Süd.
Warum ich nun auch noch die Variante mit 28° Nord/Süd hinzugefügt habe, lest Ihr weiter unten.

Die ununterbrochene Variante von Philbrick Sinu-Mollweide. Sie wurde oben schon gezeigt – ich muss gestehen, ich kann mich nicht erinnern, warum ich sie damals nicht zusammen mit der unterbrochenen Variante online gestellt habe.

Hey, eine Wagner-Variante! Ganz was neues! 😉
Diese Variante (die ebenfalls schon oben gezeigt wurde) liegt irgendwo zwischen dem Wagner BCW-A I und Canters Optimierung des Wagner IX. Die Böhm-Notation^[5] der Variante lautet Wagner vii@65-76-60-40-168, ~~und aus Gründen der Einfallslosigkeit übernehme ich das einfach als Namen der Projektion~~ seit dem 26.3.2021 trägt er seinen endgültigen Namen Wagner BCW-A III.

Diese Wagner-Variante hat eigentlich nichts Besonderes zu bieten, außer… nun, sie gefällt mir einfach.
Um diesen Entwurf in Geocart zu erzeugen, wähle den generalized Wagner mit den folgenden Parametern:
a = 2.16538, b = 1.4769, m = 0.975032, m2 = 0.75955, n = 0.422222
Verwendung in d3-geo-projection:
d3.geoWagner().poleline(65).parallels(76).inflation(40).ratio(168)
Werfen wir einen Blick auf die Verzerrungs-Eigenschaften und machen dann weiter:

Korrekturen

Vor mehr als vier Jahren habe ich Pattersons Zylinderentwurf hinzugefügt – aber die Grafiken, die ich gezeigt habe, waren falsch! 😱

Die Kartenprojektions-Software, mit der ich die Patterson-Grafiken erzeugt hatte (G.Projector), hatte leider einen kleinen Fehler, also wurde der Entwurf mit einem Seitenverhältnis von ungefähr 0,61 ausgegeben und nicht 0,57 wie spezifiziert. Die fehlerhaften Grafiken wurde ersetzt. Aktuelle Versionen von G.Projector erzeugen ebenfalls einen korrekten Patterson.
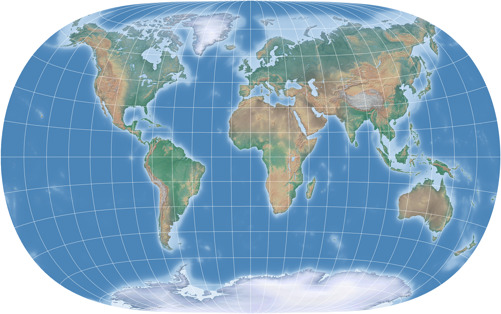
Und weil ich gerade dabei war, habe ich die alte topographische Karte im Patterson-Artikel durch eine neue ersetzt, die ich viel schöner finde.

Nun hatte ich damals aber zu Vergleichszwecken auch die Rektangularprojektion (auch rechteckige Plattkarte genannt) mit den Schnittparallelen auf 35,6° Nord/Süd hinzugefügt, welche die gleichen Seitenverhältnisse aufweist wie der falsche Patterson. Nun stand ich also vor der Wahl, entweder die alte Variante durch die neue zu ersetzen oder eine zusätzliche Variante der Plattkarte einzufügen, deren Seitenverhältnisse dem richtigen Patterson entsprechen (nämlich mit den Schnittparallelen 28°). Ich habe mich für letzteres entschieden; hauptsächlich weil ich denke, dass die Variante mit Schnittparallelen im Mitt-Dreißiger-Bereich sich eher dazu eignet, ein Blatt in Standardformaten (A0, A1, A2, …) zu füllen und Platz für eine kleine Legende zu lassen.

🌐

Die nächste Korrektur kann in einem einzigen Satz abgehandelt werden: In den Grafiken der Dymaxion-Projektion wurden einige Gradnetzlinien fehlerhaft dargestellt – dank einer neuen Version von Justin Kunimunes Kartenprojektions-Software konnte dies behoben werden.

🌐

Vor zwei Jahren habe ich angefangen, neue Grafiken für die tissot’sche Indikatrix zu verwenden – allerdings nur für neu hinzugefügte Projektionen. Jetzt habe ich auch einige alte Grafiken durch die neue Darstellung ersetzt. Und zwar jene, die weiter oben gezeigt wurden (Winkel Tripel, Ginzburg V, …).

Fußnoten

↑ Philippe Rivière: Bertin Projection (1953) (engl.)
visionscarto.net/bertin-projection-1953
↑ Demonstration der Umwandlung der Briesemeister- zur Bertin-Rivière-Projektion:
bl.ocks.org/Fil/5b9ee9636dfb6ffa53443c9006beb642
↑ János Györffy: Minimum distortion pointed-polar projections for world maps by applying graticule transformation (engl.)
doi.org/10.1080/23729333.2018.1455263
↑ Györffy verwendet in seinem Text Kleinbuchstaben, um die Projektionen zu kennzeichnen, aber ich fand ich Verwendung von Großbuchstaben besser lesbar.
↑ Wagners Umbeziffern und die Böhm-Notation:
kartenprojektionen.de/wagner-umbeziffern.php