Canters und Györffy vervollständigt, eigene Projektionen

Fr, 26.3.2021 Canters und Györffy vervollständigt, eigene Projektionen

Heute gibt es:
– neun Projektionen, die ich schon lange hinzufügen wollte,
– eine, um die ich gebeten worden bin,
– zwei neue Projektion von mir selbst, damit einhergehend zwei Namensänderungen.

Canters-Projektionen vervollständigt

Ich habe die letzten fehlenden Canters-Projektionen für Weltkarten hinzugefügt. Noch einmal möchte ich darauf hinweisen, dass ich bei den Benennungen Dr. Böhms Auflistung folge, die Gründe dafür habe ich in einem Artikel vor einigen Jahren angegeben. In dieser Auflistung wurden einige Nummern übersprungen, scheinbar fehlende Projektionen (wie W03 bis W05 usw.) existieren nicht.
Bitte beachten: Die hier gezeigte Ausführung des W23 entspricht nicht 100%ig dem Original, kommt ihm aber sehr nahe. Näheres dazu (und zu den anderen neuen Canters-Projektionen) findet Ihr im zweiten Teil von »Die Canters-Projektionen«.

Györffy-Projektionen vervollständigt

Vor zwei Jahren Jahren habe ich den Györffy E auf meine Webseite aufgenommen – aber János Györffy hat fünf Projektionen vorgestellt^[1], nämlich A, B, D, E und F (die Variante C wurde vom Urheber verworfen und wird daher auch hier nicht gelistet).
Nun habe ich alle fünf im Angebot – und irgendwann in Zukunft werde ich auch noch ein bisschen mehr über sie schreiben.

Konische Karte in südlicher Ansicht

Auf eine einzelne Anfrage habe ich eine südliche Ansicht der 20/60 Längentreuen Kegelprojektionc hinzugefügt. Vermutlich würde sie niemand für eine Weltkarte nutzen wollen. Wenigstens zeigt dieses Beispiel, dass konische Karten selten zu empfehlen sind, um den gesamten Globus abzubilden, sie spielen ihre Stärken bei Regionalkarten aus.

Der CW09 Copycat

Vor einiger Zeit habe ich einen Nachahmer des Frančula XIII vorgestellt – hier nun das gleiche Verfahren mit dem Canters W09: Eine fast identische Außenform der Projektion, aber anstelle des Wagner IX wurde der Wagner VIII als Eltern-Projektion genommen, das Ausmaß der Flächenvergößerung wurde reduziert. Und fertig ist der, der CW09 Copycat:

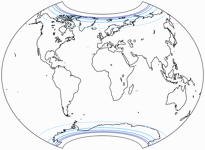
Sehen wir uns die Verteilungen der Verzerrungen im Vergleich zum Original an – zuerst die Flächenverzerrungen:

Die Linien werden gezeigt für eine Flächenvergrößerung (in Bezug auf den Wert in der Kartenmitte) von:
1,5;
2,0;
2,5;
3,0;
und 3,5.

Du siehst, dass die Flächenvergrößerungen beim CW09 Copycat tatsächlich geringer ausfallen. Darüber hinaus gefällt mir die Verteilung der Verzerrungen besser – wie bei allen Varianten des Wagner VII/VIII verlaufen die Linien entlang der Breitenkreise. Dies erleichtert die Erklärung der Verhältnisse. Wenn man danach gefragt wird, braucht man nur zu sagen: Die Projektion ist entlang des Äquators flächentreu, mit jedem Breitengrad steigt die die Flächenvergrößerung.

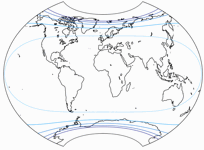
Okay, höchstwahrscheinlich wirst Du nie gefragt werden. Das ist also ein eher kleiner Vorteil, und der hat auch noch seinen Preis. Sehen wir uns die Winkelverzerrungen an:

Die Isolinien werden gezeigt für eine maximale Winkelverzerrung von:
10°,
20°,
30°,
40°,
50°,
und 60°.

Während man noch darüber streiten kann, welche Verteilung in der Kartenmitte vorzuziehen ist, macht der Canters W09 auf dem Rest der Karte die deutlich bessere Figur. Und für Australien braucht man nicht einmal mehr die Isolinien um festzustellen, dass es beim Nachahmer stärker verzerrt ist.

Summa summarum bleibt das Original wohl die bessere Projektion. Nichtsdestoweniger ist der Nachahmer auch keine schlechte Projektion, nach dem Vergleichsschema von Goldberg und Gott schneidet er besser ab als der Winkel Tripel.
Vergleiche Canters W09 und CW09 Copycat

Wagner BCW-A I, II und III

Der Wagner BCW-A, den ich vor zwei Jahren vorgestellt habe, wurde umbenannt in Wagner BCW-A I (das ist die römische Zahl 1, nicht der Großbuchstabe von i).
Der Wagner vii@65-76-60-40-168, den ich vor einem Jahren vorgestellt habe, wurde umbenannt in Wagner BCW-A III – er hatte einen eingängigeren Namen verdient, denn unter meinen eigenen »Nicht-Nachahmer«-Projektionen hat er nach verschiedenen Messverfahren (nämlich Airy-Kavraiskiy, Goldberg & Gott, Capek’s Q) die günstigsten Verzerrungswerte.
Und wie Du es jetzt sicher schon ahnst, gibt es eine neue Variante, die ich Wagner BCW-A II genannt habe:

Warum aber hat die neue Variante die Zahl II bekommen, obgleich die Projektion, welche nun die III erhält, früher vorgestellt wurde? Nun, als ich die Werte der Böhm-Notation^[2] und ihr aussehen betrachtet habe, fand ich diese Reihenfolge einfach logischer:

Projektion	Böhm-Notation
Wagner BCW-A I	67-80-60-27-190
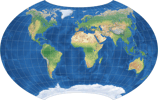
Wagner BCW-A II	65-85-60-35-185
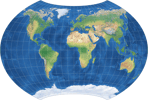
Wagner BCW-A III	65-76-60-40-168

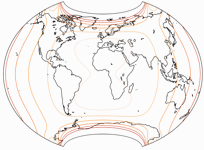
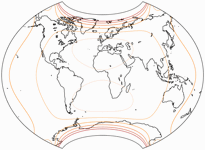
Zusammenfassend kann man sagen, dass der BCW-A II eine stärkere Krümmung der Breitenkreise aufweist als die beiden anderen – was die Flächenvergrößerung und die horizontale Kompression angeht, so fallen diese Werte jeweils stärker als bei I, aber schwächer als bei III aus.
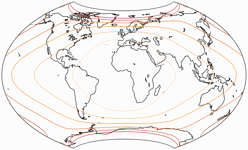
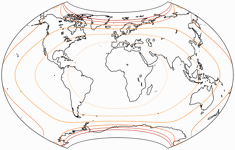
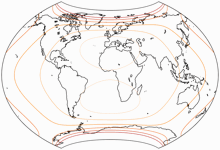
Sehen wir uns die Flächenvergrößerung (in Bezug auf den Wert in der Kartenmitte) der drei Varianten an:

So. Es gab zwar noch drei oder vier Projektionen, die ich hinzufügen wollte, aber für ein Update reicht das. Die anderen müssen sich noch ein bisschen gedulden.
Bis bald!

Quellenangaben

↑ János Györffy: Minimum distortion pointed-polar projections for world maps by applying graticule transformation (engl.)
doi.org/10.1080/23729333.2018.1455263
↑ Wagners Umbeziffern und die Böhm-Notation:
kartenprojektionen.de/wagner-umbeziffern.php

Permalink