Nachschlag: Zwei weitere Lee-Varianten

Sa, 20.8.2022 Nachschlag: Zwei weitere Lee-Varianten

Aktualisiert: Fr, 9.9.2022

Vor drei Wochen habe ich das Original und zwei Umgestaltungen der winkeltreuen tetraedrischen Projektion von L.P. Lee vorgestellt. Und vor ein paar Tagen fiel mir ein, dass es noch zwei weitere Varianten gibt. Beide arrangieren die vier Seiten von Lee’s Tetraeder, so dass sie die Erde in einem halben regelmäßigen Sechseck (Hexagon) zeigen, aber verwenden unterschiedliche Projektionszentren.

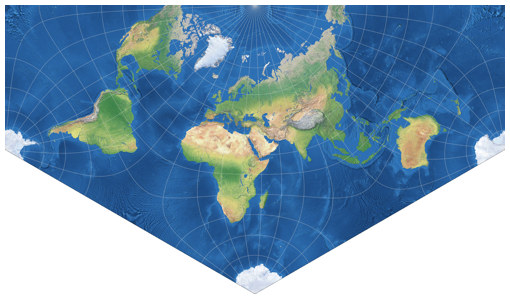
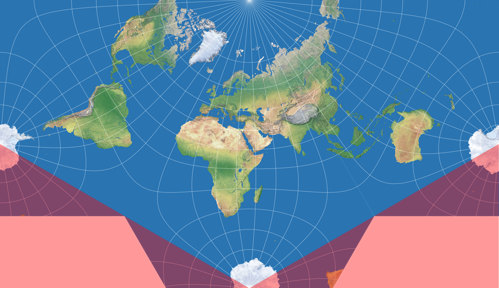
Die erste habe ich auf Carlos Furutis Website gefunden. Sie wurde 2004 von Constant Xarax aus Griechenland vorgestellt^[1] und verwendet den originalen südpolaren Aspekt, zentriert auf 20°W. Die Positionen der Kontinente erscheinen so immer noch recht vertraut im Vergleich zu Standardkarten, obgleich Alaska vom Rest des nordamerikanischen Kontinents getrennt und Antarktika in drei Teile aufgeteilt wird.
Furuti hat die Projektion »Xarax’ Welt in einem halben Hexagon« genannt, aber ich habe sie meiner Projektions-Kollektion unter dem Namen Lee-Xarax hinzugefügt.

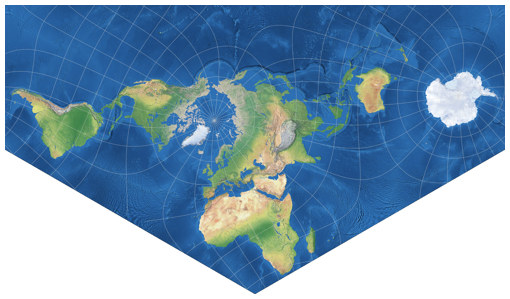
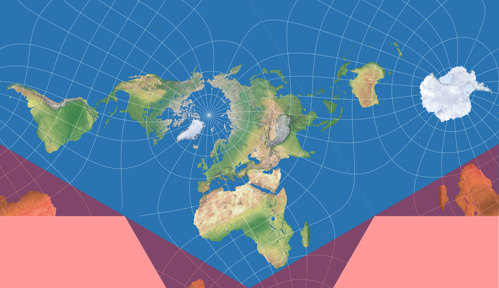
Die zweite wurde der Öffentlichkeit 2020 im Mapthematics-Forum vorgestellt, in einem Posting des Urhebers Luca Concialdi. Die Positionierung der Kontinente ist sicherlich ungewöhnlich, zeigt sie aber ohne Unterbrechungen und hält die Verzerrungen sehr gut von den Landflächen fern. Concialdi hat beim Anfertigen seiner Variante nicht an Xarax’ frühere Arbeit gedacht, schließt aber nicht aus, dass er sich evtl. unbewusst an sie erinnert hat.^[2]
Er selbst hat den Namen »Lee conformal tetrahedral projection – Concialdi rearrangement« vorgeschlagen, aber da dies ein bisschen zu lang für die Liste auf meiner Website ist, hat er der Bezeichnung Lee-Concialdi zugestimmt.

Hier sind sie also:

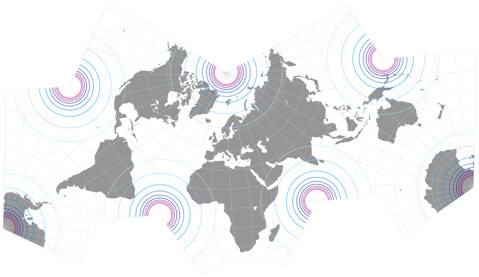
Kommen wir zu üblichen Darstellung der Verzerrungen, in diesem Fall also der Flächenvergrößerungen. Neben den beiden neuen Projektionen führe ich auch noch einmal die kürzlich vorgestellten Lee-Varianten Markley und CALM auf; aber ich werfe auch noch Concialdis früheres Werk, den Cahill-Concialdi, den ich Anfang 2019 vorgestellt habe, mit in den Ring (obgleich dieser nicht auf einer tetraedrischen, sondern einer oktaedrischen Projektion basiert).
Die Linien stehen für Werte von
1,2; 1,5; 2,0; 2,5; 3,0; 3,5; 4,0; 4,5; und 5,0:

Dieses Mal verzichte ich auf die Kommentare vom Typ »dies ist besser hier und jenes ist besser dort« und überlasse dir die Analyse. Ich beschränke mich darauf, festzustellen, dass beide eine sehr vorteilhafte Verteilung der Flächenvergrößerungen zeigen, leider begrenzt ihre äußere Form begrenzt wohl die Möglichkeiten der praktischen Verwendung. Nichtsdestoweniger denke ich, dass beides gelungene winkeltreue Weltkarten darstellen.

Ich habe die Besprechung absichtlich kurz gehalten – denn nun möchte ich noch die Konstruktion der beiden Karten beschreiben, und das dauert ein bisschen länger…

Konstruktion von Lee-Xarax & Lee-Concialdi

Derzeit scheint es keine Software zu geben, welche eine der beiden Projektionen »fertig konfektioniert« erzeugen kann.
[Update 9.9.2022: Es gibt doch eine Software, siehe unten.]
Aber es gibt mindestens zwei Programme, die Lee’s winkeltreue tetraedrische Projektion im Angebot haben, so dass man die Varianten von Xarax und Concialdi selbst zusammensetzen kann: Geocart (kommerziell) und MapDesignerRaster (gratis). Die ersten Schritte unterscheiden sich in diesen beiden.

MapDesignerRaster erzeugt eine Darstellung der gesamten Erde in Lee’s Projektion. Wähle die Projektion Lee tetrahedral (triangular) aus. Für Lee-Xarax lauten die Konfigurations-Paramter:
Latitude: 90 Longitude: -20 Ctr. Meridian: 0

Für Lee-Concialdi sind folgende Werte zu verwenden:
Latitude: 37 Longitude: 168 Ctr. Meridian: -81

Sichere die Datei als PNG-Bild und öffne sie mit einem Grafikprogramm. Nun musst du das gleichseitige Dreieck in vier kleinere gleichseitige Dreiecke zerschneiden. Das mittlere muss dann noch in drei gleichschenklige Dreiecke von gleicher Größe unterteilt werden.

Schnittkanten in den Projektionen Lee-Xarax (links) und Lee-Concialdi:
Schneide zuerst entlang der durchgezogenen Linien.
Dann unterteile das mittlere Dreieck entlang der gepunkteten Linien.

Ich zeige später, wie man die Einzelteile zusammensetzt. Vorher möchte ich aber die ersten Schritte in Geocart zeigen. Wie ich schon im eingangs erwähnten Blogpost schrieb, erzeugt dieses Programm die vier Seiten des Tetraeders separat.

Erzeuge eine neue Karte mit der Projektion polyhedral conformal face. Rufe den Dialog »Projection Parameters« auf, wähle im Menü »Platonic solid« den Eintrag tetrahedron.
Setze das »Face« auf 0.
Dann rufe den »Projection Center«-Dialog auf. Für Lee-Xarax musst du folgende Werte eintragen:
Latitidinal: 90°S Longitudinal: 20°W Transversal: 0°
Für Lee-Concialdi:
Latitidinal: 37°S Longitudinal: 12°W Transversal: 99°

Kopiere die Karte und füge sie dreimal ein.
Trage bei den drei Kopien im »Projection Parameters«-Dialog die Werte 1, 2 und 3 ein.
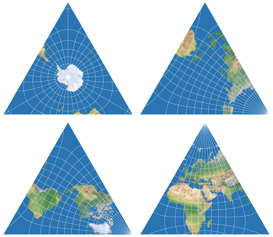
Dein Dokument sollte jetzt in etwa so aussehen:

Das mittlere Dreieck (welches bei Lee-Xarax den Südpol enthält und bei Lee-Concialdi Teile von Antarktika, Südamerika und Afrika) muss nun, wie oben gezeigt, in drei gleiche Teile geschnitten werden.

Unabhängig davon, welches Programm du benutzt hast, solltest du nun alle sechs Teile des Puzzles haben. Füge sie nach dem folgenden Schema zusammen (hier nur für Lee-Xarax gezeigt; ich denke, du wirst herausfinden, welche Teile der Lee-Concialdi-Projektion wo hin zusetzen sind):

Für mich war es am schwierigsten, den mittleren Teil zu dritteln. Hier sind also zwei alternative Herangehensweisen. Die erste funktioniert nur in Geocart und ist nur auf den Lee-Xarax anwendbar.

Dir ist vielleicht aufgefallen, dass die Schnittkanten exakt entlang gewisser Meridiane verlaufen. Das versetzt uns in die Lage, die Dreiteilung vom Programm vornehmen zu lassen. Du brauchst drei Kopien des mittleren Teils. Rufe den »Boundaries«-Dialog für alle drei nacheinander auf.
Stelle sicher, dass der Button »Boundaries are defined relative to the graticule« angekreuzt ist.
Trage bei allen drei die Boudaries North: 15°S und South: 90°S ein.^[3]
Für die östlichen und westliche Begrenzungen musst du bei jeder Kopie unterschiedliche Werte einsetzen, nämlich
West: 20°W und East: 100°E,
West: 100°E und East: 140°W, sowie
West: 140°W und East: 20°W.
Und voilà, schon hast du die benötigten Drittel!

Die andere Alternative funktioniert mit beiden Projektionen und den Resultaten von beiden Programmen. Anstatt den Mittelteil zu zerschneiden, dupliziert man ihn zweimal und fügt die Einzelteile dann so zusammen:

Nachdem du sie nahtlos zusammengesetzt hast, entferne die nicht benötigten Teile links, rechts und unten. Beim Lee-Xarax ist das recht einfach, denn alle Schnitte müssen direkt durch den Südpol verlaufen:

Beim Lee-Concialdi gibt es keine derart praktische visuelle Hilfe, also muss man ein bisschen rechnen. Sofern dein Bild irgendwelche Ränder um die eigentliche Projektion herum aufweist, entferne sie zuerst. Dann schneide rechts und links jeweils ein Sechstel der Breite des Bildes ab, und ein Drittel am unteren Rand:

Als letztes muss man zwei dreieckige Bereiche entfernen. Dies kann problematisch sein, weil es in vielen Programmen keine dreieckiges Auswahlwerkzeug gibt. Ich habe mir folgendermaßen beholfen: Ich habe die Datei in einem Vektorgrafikprogramm geöffnet (Adobe Illustrator, Affinity Designer, PhotoLine, Inkscape etc.) und habe zwei Dreiecke über die Grafik gezeichnet. Die Scheitelpunkte müssen in den unteren Ecken links und rechts, in der vertikalen Mitte am linken und rechten Rand und in der horizontalen Mitte am unteren Rand liegen. Abermals liegen diese Punkte beim Lee-Xarax genau auf dem Südpol. Hier folgt ein Beispiel für beide Projektionen, mit roten halbtransparenten Dreiecken. Tatsächlich sollten sie natürlich undurchsichtig und mit der gewünschten Hintergrundfarbe gefüllt sein:

Puh! Wir sind durch!
Ein Tipp noch: Die Teile wirklich nahtlos zusammenzusetzen, ist nahezu unmöglich – oder ich stelle mich dabei besonders dumm an. Kann auch sein. Aber ich empfehle, eine Karte zusammen zu basteln, die deutlich größer ist als du es eigentlich brauchst, und die dann auf die gewünschte Größe runter zu skalieren. Mit ein bisschen Glück wird das die Nahtstellen verstecken. Für ein perfektes Ergebnis musst du u.U. etliche Pixel »reparieren«…

P.S.: Ich hatte diesen Blogpost gerade fertig geschrieben, da habe ich gesehen, dass Lee’s winkeltreue tetraedrische Projektion auch für D3 verfügbar ist, nämlich in d3-geo-polygon. Mit Hilfe der Observable-Demo habe ich herausgefunden, dass man den Aspekt für Lee-Xarax mittels .rotate([-40, 0]) erzeugt. Die richtige Eingabe für den Lee-Concialdi konnte ich noch nicht ermitteln und werde da wohl auch nicht weiterforschen. Falls jemand anders sie findet, bitte ich um eine entsprechende Mitteilung. Wie auch immer, die Konstruktion der fertigen Karte entspricht dann der oben gezeigten Vorgehensweise für Grafiken aus MapDesignerRaster.

🌐

Update 9.9.2022:
Constant Xarax hat mich auf das Photoshop-Plugin Flexify aufmerksam gemacht, welches eine breite Palette von Projektionen erzeugen kann (auch wenn viele von ihnen nur zu dekorativen Zwecken dienen), darunter Lee-Xarax (dort einfach nur Xarax genannt). Ich habe Photoshop nicht, aber nach dem Download der freien Test-Version des Plugins konnte ich feststellen, dass es auch in den Programmen PhotoLine und Affinity Photo funktioniert. Und da Flexify auch Einstellungen für Latitude, Longitude und Spin anbietet, sollte man auch in der Lage sein, den Lee-Concialdi anzufertigen. Ich sage »sollte«, denn ich war nicht in der Lage, die exakten Werte für diese Variante zu ermitteln.

Lee-Xarax wird gerendert, wenn man als Output »Xarax« einstellt und wie Werte von Latitude, Longitude und Spin bei 0 belässt. Das unterscheidet sich natürlich von den Werten, die ich oben genannt habe, aber ich denke, dies ist nachvollziehbar, denn in diesem Fall bedeutet das einfach »verwende das Standard-Zentrum dieser Projektion«.

Um also Lee-Concialdi zu erzeugen, erschien es mir logisch, die Abweichung des Projektionszentrums von dem des Lee-Xarax einzugeben. Leider hat das nicht funktioniert. Die beste Annäherung, die ich finden konnte (die aber immer noch nicht korrekt ist), habe ich mit folgenden Werten erzeugt:
Latitude: 53 Longitude: -13,795 Spin: 1,5

Eine logischer Erklärung habe ich dafür nicht, aber – soweit ich das sagen kann – braucht man tatsächlich Werte mit Nachkommastellen, um beim Lee-Concialdi anzukommen. Und darin liegt ein Problem, denn jedesmal, wenn ich Bruchwerte eintippen wollte, schien eine Art von Eingabekorrektur anzuspringen und änderte z.B. -13,8 in -138 um oder 1,5 in 1. Ich habe keine Ahnung, ob das ein genereller Fehler des Plugins ist, oder ob es daran liegt, dass ich es nicht aus Photoshop heraus aufrufe. Auf jeden Fall bestand für mich die einzige Möglichkeit, zwei Bruchwerte einzugeben, darin, sie nicht einzutippen, sondern sie über die Schieberegler einzustellen. Aber dann ist es ziemlich unmöglich, genaue Werte zu setzen. Darum sieht man beim obigen Screenshot auch -13,795: Eigentlich wollte ich -13,8 ausprobieren, aber ich war schon froh, dass ich in der Nähe gelandet war.

Also habe ich die Versuche, Lee-Concialdi korrekt zu rendern, eingestellt. Aber ich denke, dass es möglich ist. Irgendwie. Der Vorteil des Flexify-Plugins liegt auf jeden Fall darin, dass man sich die oben gezeigte Arbeit (Schneiden, Zusammenfügen, Verstecken der Nahtstellen) sparen kann. Aber denk daran, dass es sich hier um ein graphisches Werkzeug handelt, eine kartographische oder GIS-Software. Wenn du also eine echte Karte mit Beschriftungen für Länder, Städte oder physische Merkmale erstellen willst, kannst du Flexify verwenden, um die Hintergrundgrafik zu erzeugen – der Rest muss aber von Hand erledigt werden.

Aber in einem Blogpost über die Lee-Xarax- und Lee-Concialdi-Projektionen ist das Flexify-Plugin natürlich einer Erwähnung wert.

Quellenangaben / Fußnoten

↑ Leider hat Furuti nicht die Quelle von Xarax’ Vorschlag genannt. Wenn irgendjemand mehr darüber weiß, bitte sagt mir Bescheid!
↑ Zitiert nach persönlicher Kommunikation im August 2022.
↑ Genau genommen ist North: 15°S nur ein Beispiel. Die Sache funktioniert mit jedem Breitengrad, der über seine gesamte Länge hinweg außerhalb des gegebenen Dreiecks liegt.

Permalink