Mo, 3.6.2019 Vier winkeltreue polyedrische Projektionen und mehr
Heute habe ich der Liste auf meiner Website sechs Projektionen hinzugefügt.
Wie der Titel dieses Blogposts schon verrät, gehören vier davon der Gruppe der Polyedrischen an und sind winkeltreu.
Beginnen wir aber mit dem »und mehr«.
Die zylindrische Zentralprojektion
Die zylindrische Zentralprojektion[1] wollte ich eigentlich gar
nicht auf die Website aufnehmen, weil ihr kartografischer Wert… nun ja, sagen wir mal: nicht allzu hoch einzuschätzen ist.
Genauer gesagt, ist sie für kartografische Zwecke eigentlich gar nicht zu gebrauchen.
Also, wozu ist sie überhaupt gut?
Zum einen kann man anhand dieser Projektion die Grundidee einer Zylinderprojektion sehr gut erklären:
- Pack eine Lichtquelle in das Zentrum des Globusses.
- Wickle einen Zylinder aus Papier um den Globus, welcher den Globus am Äquator berührt.
- Schalte das Licht ein.

Schematische Konstruktion der zylindrische Zentralprojektion[2]
Und voilà! Die zylindrische Zentralprojektion wird auf das Papier geworfen!
»Moment!«, mögen jetzt einige Leute rufen, »Ich habe mal gehört, dass die Mercator-Projektion auf diese Weise konstruiert wird!«
Ja, möglicherweise hast Du das mal gelesen oder gehört (z.B. in einer
kürzlich ausgestrahlten Folge von Terra X). Aber sorry, das ist falsch.
Die Mercator-Karte kann nicht mit Hilfe einer perspektivischen Projektion konstruiert werden.
Wenn Du mir nicht traust, überprüfe das in der englischen Wikipedia.
Wenn Du Wikipedia nicht traust, überprüfe das in der (englischen)
Liste der Projektionen auf mapthematics.com,
verfasst von Daniel »daan« Strebe, Autor einer Kartenprojektions-Software und Verfasser diverser Fachartikel zum Thema Kartenprojektionen.[3]
Wenn Du Daniel Strebe nicht traust, überprüfe das in der sehr ausführlichen
Abhandlung von Friedrich W. Krücken, in der er sich mit der Frage befasst, wie Gerhard Mercator
überhaupt in der Lage war, seine Projektionsmethode zu konstruieren.
Kommen wir zur zylindrischen Zentralprojektion selbst zurück: Die Projektionsmethode, so einfach sie auch ist, hat einen gewaltigen Nachteil: Sowohl Winkel-, als auch Größenverzerrung werden gigantisch, wenn man sich den Polen nähert. Und zwar so gewaltig, dass ich sie, um ein halbwegs vernünftiges Bild für die Darstellung auf der Website zu erhalten, bei 75° Nord/Süd abgeschnitten habe:
Wenn Du einen größeren Ausschnitt des Projektionsbildes sehen willst: Das zeige ich noch am Ende des Blogposts.
Und nachdem ich all das gesagt habe, wundert es Dich vielleicht nicht mehr, dass es einen
Verwendungszweck gibt, bei dem diese Projektion regelmäßig zum Einsatz kommt:
Um zu zeigen, dass die Mercator-Projektion nicht perspektivisch erzeugt wird.
Da diese Behauptung immer noch herumgeistert, fühlte ich mich verpflichtet, die
zylindrische Zentralprojektion auf die Website aufzunehmen.
Kommen wir nun zu den meiner Meinung nach interessanteren Neuzugängen.
Die Dymaxion-Karte
Hier haben wir nun die erste polyedrische Karte für heute, die aber nicht winkeltreu ist.
1943 stellte der Architekt und Designer Buckminster Fuller diverse Weltkarten vor, die als flache Karte
genutzt werden, aber auch zu einer dreidimensionalen Globus-Annäherung zusammengefaltet werden konnten.
1954 folgte dann die Variante, die wahrscheinlich die einzige ist, welche einen gewissen Bekanntheitsgrad erreichen konnte.
Bei dieser wird die Welt auf ein Ikosaeder projiziert.
Obwohl Fuller das Wort »Dymaxion« meines Wissens für alle Varianten benutzte, ist heutzutage damit üblicherweise
die hier gezeigte Ikosaeder-förmige gemeint, welche manchmal auch »Fuller-Projektion« oder »Airocean-Map« genannt wird.
Sie reduziert sowohl Winkel-, als auch Flächenverzerrungen, aber ist weder winkel-, noch flächentreu. Fuller gab die Nord/Süd-Ost/West-Ausrichtung üblicher Weltkarten absichtlich auf, aber möglicherweise ist das genau der Grund, warum sie vergleichsweise selten verwendet wird.
Ich bitte die unterbrochenen Gradnetz-Linien in der Nähe der Pole zu entschuldigen. Dabei handelt es sich natürlich nicht um einen Mangel der Dymaxion-Karte, sondern nur um ein Problem in der Art und Weise, auf die ich die Projektionsgrafiken erzeugt habe.
Das war der »und mehr«-Abschnitt – nun geht es weiter mit den vier winkeltreuen polyedrischen Projektionen.
Cahills winkeltreuer (konformer) Schmetterling
Schon vor einer Weile habe ich einige polyedrische Projektionen
vorgestellt, die sich auf die Arbeit von Bernard J.S. Cahill bezogen, darunter der Cahill-Concialdi,
welcher ein neues Arrangement von Cahills Ende der 1920er Jahre vorgestellter winkeltreuer (oder konformer)
schmetterlingsförmiger Projektion darstellt.
Hier ist nun Cahills Original:
Um Verwechslungen zu vermeiden: 1909 stellte Cahill seine erste Schmetterlings-Karte vor, welche
aber weder flächen- noch winkeltreu (somit also vermittelnd oder aphylaktisch) war. Diese
Variante kann ich leider nicht zeigen, da sie von keiner mir bekannten Kartenprojektions-Software erzeugt werden kann.
Die hier gezeigte winkeltreue Variante wurde dann etwa 20 Jahre später vorgestellt, die zugehörigen mathematischen
Formeln wurden auf Cahills Anregung von Oscar S. Adams entwickelt.
Die Aufgabe, die schlimmsten Größenverzerrungen von den Landmassen wegzuhalten, wird gut erfüllt:
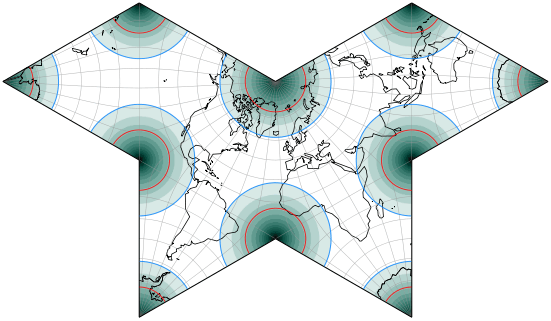
Dunklere Grüntöne stehen für größere Flächenverzerrungen.
Die blaue Linie zeigt eine 1,2-fache Vergrößerung an, die rote eine 2-fache.
In einigen Zeichnungen hat Cahill die Projektion auf 157°30′ Ost zentriert, so dass Afrika im linken »Flügel« dargestellt wird:
Cahills winkeltreue M-förmige Projektion
Hier muss gar nicht viel gesagt werden, denn es handelt sich einfach um ein anderes
Arrangement von Cahills konformen Schmetterling, welches erzeugt werden kann, indem
man die Schmetterlings-Projektion auseinander schnippelt und anders wieder zusammensetzt.
Ich bevorzuge dieses Arrangement, weil es den Weltkarten, die wie sie üblicherweise sehen, ähnlicher ist.
Mehr Informationen über Cahills winkeltreue Projektion sind (leider nur auf Englisch) nachzulesen unter
genekeyes.com/CAHILL-VARIANTS/Cahill-Conformal.html.
Dymaxion-ähnliche konforme Projektion
Auf Basis der Mathematik von Oscar S. Adams (ab 1925) und L.P. Lee (1976) hat Daniel »daan« Strebe 2019 eine winkeltreue Variante von Fullers Dymaxion-Karte (s.o.) vorgestellt.
Und ich muss sagen, dass mir diese Variante besser gefällt als das Original.
Warum?
Erstens weisen die Gradnetzlinien nicht die Knicke auf, die typisch für das Original sind:
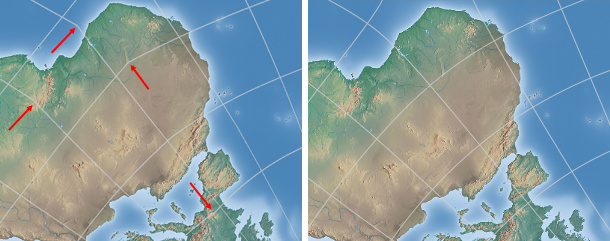
Knicke in den Gradnetzlinien der Dymaxion-Karte (links) im Gegensatz zu den
ungeknickten Linien der Dymaxion-ähnlichen konformen Projektion.
Und zweitens – sie ist winkeltreu.
Versteht mich nicht falsch, ich denke nicht, dass konforme Projektionen den vermittelnden grundsätzlich überlegen sind,
aber wenn man die Wahl hat zwischen einer Projektion, die eine metrische Eigenschaft aufweist (heißt, sie ist entweder
winkel- oder flächen- oder längentreu), und einer sehr ähnlichen vermittelnden Projektion, dann sollte die
vermittelnde einen deutlichen Vorteil aufweisen, damit man sich für diese entscheidet.
(Das ist natürlich nur meine Meinung.)
Und die Sache ist die: Ich sehe keinen derartigen Vorteil in der originalen Dymaxion-Karte.
Sie hat wahrscheinlich ein geringes Ausmaß an Flächenvergrößerungen (obwohl ich das nicht sicher sagen kann,
weil ich leider nicht über die Hilfsmittel verfüge, um die beiden Projektion diesbezüglich angemessen zu vergleichen),
aber ist das genug, um einen Unterschied zu machen? Ich weiß es nicht. Aber was ich weiß: Die
Dymaxion-ähnliche konforme Projektion hat schon sehr niedrige Vergrößerungswerte. Seht Euch das selbst an:

Dunklere Grüntöne stehen für größere Flächenverzerrungen.
Die blaue Linie zeigt eine 1,2-fache Vergrößerung an, die rote eine 2-fache.
Das ist wirklich keine ausufernde Flächenvergrößerung. Ich bezweifle, dass es sinnvoll ist, nach einer weiteren Reduktion der Vergrößerung zu streben (ohne aber echte Flächentreue zu erreichen), auf Kosten der Formen der Kontinente, die in meinen Augen bei der winkeltreuen Variante besser dargestellt werden: Direkter Vergleich der originalen Dymaxion-Karte und der Dymaxion-ähnlichen winkeltreuen Projektion
Winkeltreue Chaiselonge-Projektion
Noch eine winkeltreue Projektion auf ein Ikosaeder, ebenfalls von daan Strebe (2019). Auch hier werden die gröbsten Verzerrungen von den Landmassen ferngehalten; abgesehen von der arabischen Halbinsel wird eine gute Kontinuität erreicht.
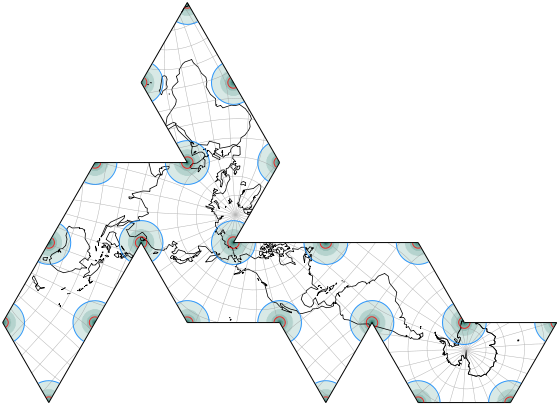
Hier ist ein kleines eigenes Experiment: Anstatt die arabische Halbinsel zu durchtrennen, schneide ich einfach durch eine der größten Landmassen, nämlich Eurasien. Schluck! Aber wenigstens geht der Schnitt… nun ja, ganz grob etwa daher, wo man üblicherweise die Grenze zwischen Europa und Asien setzt. Ich wollte es hier nur mal schnell zeigen, dieses Experiment wird nicht in die Liste auf meiner Website aufgenommen.
Hinweise zur Software
Die (originale) Dymaxion-Karte kann erzeugt werden mit Justin Kunimunes Kartenprojektions-Software.
Die winkeltreuen polyedrischen Projektionen sind in der kürzlich erschienenen Version 3.3 von Geocart enthalten.
Fußnoten
- ↑ Die deutsche Bezeichnung zylindrische Zentralprojektion habe ich selbst gewählt, als Übersetzung des üblichen englischen Begriffs Central Cylindric Projection. Andere Bezeichnungen lauten Perspektivische Zylinderabbildung (F.W. Krücken) oder Gnomonische Zylinderprojektion (R. Böhm).
- ↑ Rekonstruktion einer Illustration in K.H. Wagner: Kartographische Netzentwürfe, 1949/1962, Seite 33, Abb. 19
- ↑ Einige von Strebes Artikeln sind zugänglich auf tandfonline.com und researchgate.net.








 Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Kommentare
Sei der erste, der einen Kommentar hinterlässt!