Wagner II, lentikuläre Variante

Mi, 15.1.2020 Wagner II, lentikuläre Variante

Aktualisiert: Mo, 3.2.2020

Arrggh.
Immer wieder sagen ich, dass die Liste der Projektionen eh schon zu viele Wagner-Variationen enthält – und immer wieder füge ich dann doch wieder neue hinzu. Immerhin nehme ich mir diesmal vor, demnächst mal zu überprüfen, ob ich nicht die eine oder andere Variante rausschmeißen sollte…

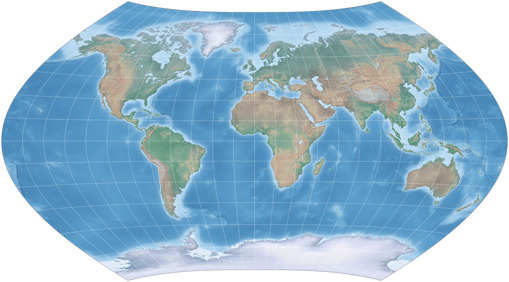
Die Idee zu den heute vorgestellten Wagner-Varianten kam mir natürlich, als ich am Januar-Blatt meines Projektionskalenders gearbeitet habe, welches des Wagner II zeigt, einen pseudozylindrischen Entwurf mit Meridianen in Form von Sinuskurven. Wie gesagt habe, gefällt mir dieser Form der Meridiane – und ich mag noch etwas, nämlich lentikuläre Projektionen, welche im Gegensatz zu den pseudozylindrischen gekrümmte Breitenkreise aufweisen. Soweit mir bekannt ist, gibt es allerdings keine lentikulären Entwürfe mit sinusförmigen Meridianen. Also wollte ich mal sehen, wie so etwas aussieht.

Mit Hilfe von Flex Projector war ich in der Lage, eine herzustellen, indem ich den Wagner II mit der Krümmung der Breitenkreise des Wagner VII gemixt habe.
Weiter unten liefere ich eine Beschreibung des Vorgangs.

Lentikulärer Wagner II

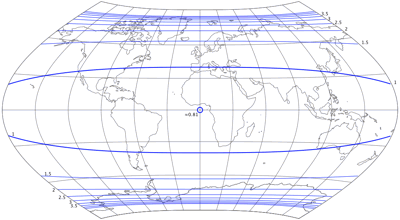
Und hier sind sie, die lentikuläre Variante vom Wagner II – sinusoidale Meridiane und gekrümmte Breitenkreise! Das Ergebnis ist sicherlich nicht spektakulär oder überraschend, aber das war auch nicht mein Ziel, ich war nur neugierig, wie diese Kombination aussieht. Und ich denke, es ist schon eine nette Alternative zum Original. Nun, gekrümmte Breitenkreise werden normalerweise nicht verwendet, weil ich sie so hübsch finde, sondern zwecks Verbesserung der Verteilung von Verzerrungen. Vergleichen wir die Verzerrungs-Darstellungen (exportiert aus Flex Projector) vom Original und der lentikulären – zunächst die Flächenverzerrungen:

Meine Variante weicht etwas mehr von der Flächentreue ab. Wie man sehen kann, beträgt der Faktor des Flächenverzerrung des Originals in der Kartenmitte 1 (= flächentreu), während die lentikuläre Version mit 0,88 leichte Flächenverkleinerungen zeigt. Zwar ist die Entscheidung, welche Flächen als vergrößert und welche als verkleinert anzusehen sind, eigentlich beliebig^[1], das ändert aber nichts daran, dass meine Version eine höhere Varianz der Flächenverzerrungen aufweist.
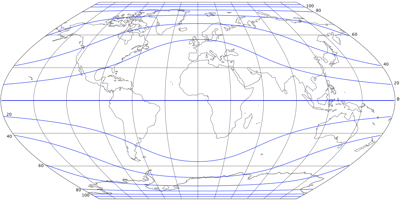
Häh? Hatte ich nicht gerade etwas von der Verbesserung der Verzerrungsverhältnisse gesagt? Richtig, das bezog sich aber auf die Winkelverzerrungen:

Die »Ecken« der Karte (Alaska, östliches Sibirien, Japan, Neuseeland) profitieren deutlich von den gekrümmten Meridianen. Da der Wagner II eine vermittelnde Projektion ist, die recht nah an der Flächentreue bleibt, schien es mir vernünftig, eine leichte weitere Abweichung der Flächen in Kauf zu nehmen, um damit die reduzierten Winkelverzerrungen zu erkaufen. Zumindest gemäß der Werte, die Flex Projector errechnet (es gibt andere Metriken, die andere Ergebnisse erzeugen mögen!), läuft das auch auf eine Gesamt-Verbesserung hinaus:

Projection	Scale	Scale Cont.	Areal	Areal Cont.	Angular	Angular Cont.	Acc.
Wagner II lenticular	0.27	0.30	0.17	0.22	23.74	24.52	82.7
Wagner II original	0.32	0.35	0.12	0.16	26.88	27.88	76.5

Hervorgehobene Werte sind besser. Erklärung der Werte siehe unten. ^[2]

Nun hatte ich also eine sinusoidale lentikuläre Projektion aussehen kann und sie hat sogar zumindest einige Vorteile zum Original. Hier kannst Du sie direkt vergleichen:
Wagner II original vs. Wagner II lentikulär
Der Link aktiviert den »Experten Modus« und springt direkt zum Vergleich »auf gleiche Breite skaliert«, der hier passender ist.

Aber noch war meine Neugier nicht befriedigt. Jetzt wollte ich auch wissen, wie lentikuläre Versionen von Wagner I und Wagner III aussehen…

Lentikulärer Wagner I.a

Das Wichtigste zuerst: Hier habe ich den originalen Wagner I abermals mit der Krümmung der Breitenkreise des Wagner VII gemixt… aber obwohl beide Projektionen flächentreu sind, gilt dies nicht für das Resultat!
Hier haben wir eine aphylaktische (= vermittelnde) Projektion. Da die Flächentreue eine wichtige Eigenschaft ist, fand ich es unpassend, für diese Variante den gleichen Namen zu verwenden – also ich sie Lentikulärer Wagner I.a genannt (mit dem a für aphylaktisch).

Projection	Scale	Scale Cont.	Areal	Areal Cont.	Angular	Angular Cont.	Acc.
Wagner I.a lenticular	0.34	0.37	0.07	0.08	28.57	29.39	76.6
Wagner II original	0.39	0.44	0.00	0.00	31.92	33.06	71.2

Hervorgehobene Werte sind besser. Erklärung der Werte siehe unten. ^[2]

Der Acc.-Wert erhöht sich nicht so stark wie beim Wagner II, was nicht erstaunlich ist, da nun eine Flächenverzerrung vorliegt. Immerhin zeigt sich trotzdem noch eine leichter Verbesserung, aber man muss sich entscheiden, ob sie es wert ist, auf die Flächentreue zu verzichten.
Ehrlich gesagt, finde ich das nicht. Wenn ich Flächentreue haben möchte, will ich auch echte Flächentreue haben. Wenn ich der Meinung bin, dass ich davon abweichen kann, kann ich direkt zum Wagner II greifen und so die Winkelverzerrungen weiter minimieren. Es wäre natürlich möglich, einen lentikulären Wagner I zu schaffen, der tatsächlich flächentreu ist. Aber leider muss ich zugeben, dass ich nicht dazu in der Lage bin.

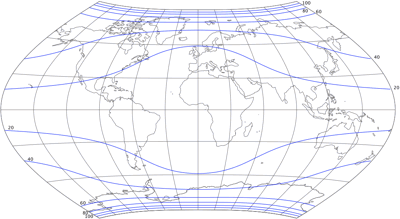
Lentikulärer Wagner III.a

Ohne groß rumzuquatschen: Abermals verliert die Projektion ihre Eigenschaft, nämlich die Abweitungstreue (= die gleichabständigen Breitenkreise) entlang des Zentralmeridians – darum habe ich auch ihr das a angehängt. Das mag etwas verwirrend sein, denn auf meiner Website habe alle Projektionen mit gleichabständigen Breitenkreisen als »vermittelnd« gelistet. Nun ja… wenigstens zeigt das Anhängsel gleich (hoffe ich), dass es außer den gekrümmten Breitenkreisen noch einen weiteren Unterschied geben muss…

Wenn einem der Wagner III aufgrund des Ausmaßes der Flächenvergrößerung gefällt, könnte die lentikuläre Variante eine gute Alternative sein. Sofern es um gleichabständige Breitenkreise geht, vergisst man den lentikulären Wagner III.a besser!

Zu den Verzerrungen:

Projection	Scale	Scale Cont.	Areal	Areal Cont.	Angular	Angular Cont.	Acc.
Wagner III.a lenticular	0.26	0.30	0.32	0.44	20.41	21.80	85.1
Wagner III original	0.28	0.32	0.30	0.43	22.68	23.82	77.9

Hervorgehobene Werte sind besser. Erklärung der Werte siehe unten. ^[2]

Résumé

So, nun weiß ich also, wie lentikuläre Projektionen mit sinusoidalen Meridianen aussehen. Das ist doch schon mal etwas.
Darüber hinaus… die Varianten von Wagner I und III verlieren (in der hier gezeigten Implementation) ihre metrischen Eigenschaften der Flächen- bzw. Abweitungstreue. Daher sehe ich sie nicht als empfehlenswerte Alternativen zu den Originalen an. Da der Wagner II keine Eigenschaften dieser Art hat, kann er sie auch nicht verlieren. 😉
Dieser gefällt mir, denn er verbessert die Verteilung der Winkelverzerrungen, während die Verschlechterung der Flächenverzerrungen nicht so ins Gewicht fällt (schließlich sind wir ja schon im Bereich der vermittelnden Projektionen).

In die Liste der Projektionen wird daher auch nur der lentikuläre Wagner II aufgenommen.

Bedenkt man die Ergebnisse einer Studie, die vor ein paar Jahren durchgeführt wurde ^[3], nach der die Leute elliptische Meridiane den sinusförmigen vorziehen, muss ich stark anzweifeln, dass außer mir selbst daran Interesse hat, eine Projektion wie den lentikulären Wagner II tatsächlich zu benutzen. Zumal ein zweites Ergebnis der Studie war, dass auch gekrümmte Breitenkreise nicht so gern gesehen sind (allerdings habe ich diese Schlussfolgerung noch nie so ganz nachvollziehen können, aber das ist ein anderes Thema).

Aber was soll’s?
Die Sache war von vornherein ein Experiment und nicht jedes Experiment endet erfolgreich. Und es gab schon andere Projektionen, die aus eher akademischen Gründen geschaffen worden sind. (Ein Beispiel davon werden wir im Juni-Teil meiner kleinen Kalender-Serie sehen.)

Wie ich sie erstellt habe

Wie eingangs angekündigt, möchte ich noch kurz zeigen, wie ich die Projektionen gemixt habe. Im Flex Projector sind folgende Schritte durchzuführen:

Wechsle in den Modus Flex Mixer.
Wähle Wagner II als erste und Wagner VII als zweite Projektion.
Ziehe den Schieberegler Parallels Bending (Krümmung der Breitenkreise) auf 100% Wagner VII.
Ziehe die drei anderen Schieberegler auf 100% Wagner II.
Mir gefiel das automatische Höhe/Breite-Verhältnis nicht, also habe ich es etwas angepasst:
Stelle Height (Höhe) auf 0.55.
Zum Schluss habe ich den Size-Knopf betätigt und Minimize Area Distortion (minimiere Größenverzerrungen) ausgewählt. Beachte, dass die nicht die eigentliche Projektion ändert, es berechnet nur den (internen) Maßstab. Dieser Schritt sollte immer zuletzt ausgeführt werden, wenn Du im Flex Projector Projektionen kreierst.

Abgesehen von der Auswahl der ersten Projektion in Schritt 2 war die Verfahrensweise die gleiche beim lentikulären Wagner I und III.

Fußnoten

↑ Zur »Beliebigkeit« von Flächenvergrößerung und -verkleinerung, siehe das (englische) Handbuch des Programms Geocart. Das Handbuch steht gratis zum Download bereit. Kapitel Distortion Visualization, Seite 9.18 (entspricht S. 140 im PDF). Lies die zweite Absätze, die beginnen mit:
To understand what these diagrams mean, note that angular deformation is absolute (…)
↑ ↑ ↑ Werte in der Verzerrungs-Tabelle – Erklärung zitiert nach den Hilfe-Dateien in Flex Projector:
Scale – Der gewichtete Mittelwert der gesamten Streckenverzerrungen.
Scale Cont. – Der gewichtete Mittelwert der gesamten Streckenverzerrungen, nur kontinentale Flächen.
Areal – Der gewichtete Mittelwert der gesamten Größenverzerrungen. 0 bei einer flächentreuen Projektion.
Areal Cont.– Der gewichtete Mittelwert der gesamten Größenverzerrungen, nur kontinentale Flächen.
Angular – Der gewichtete Mittelwert der gesamten Winjekverzerrungen. 0 bei einer winkeltreuen Projektion.
Angular Cont. – Der gewichtete Mittelwert der gesamten Winjekverzerrungen, nur kontinentale Flächen.
Acc. – Der Acceptance index. Die relative Fläche mit akzeptablen Verzerrungseigenschaften, unter Berücksichtigung von sowohl Winkel-, als auch Flächenverzerrungen.

Kontinentale Werte berechnet für Kartenzentrum auf dem Greenwich-Meridian.
Die Berechnung der Verzerrungen basiert auf Frank Canters und Hugo Decleir (1989), The World in Perspective - A Directory of World Map Projections, Wiley, Chichester, etc., Seite 181.
Der Acceptance index basiert auf Capek, R. (2001). Which is the best projection for the world map? Proceedings of the 20th International Cartographic Conference ICC, Beijing.
Online verfügbar (engl.)
↑ Bojan Šavrič, Bernhard Jenny, Denis White & Daniel R. Strebe (2015), User preferences for world map projections, Cartography and Geographic Information Science.
Online verfügbar (engl.)