Eine Handvoll asymmetrischer Projektionen

Mo, 24.1.2022 Eine Handvoll asymmetrischer Projektionen

Im Dezember habe ich zwei asymmetrische Entwürfe vorgestellt, nämlich Weia Reinbouds Cupola-Projektion und meinen eigenen asymmetrischen Wagner VII.b. Letzterer war eine Komposition aus einer nördlichen und einer südlichen Hemisphäre, die mit verschiedenen Konfigurationsparametern erstellt und dann am Äquator zusammengefügt wurden. Dabei hatte ich drei gewissen Probleme:

In der ersten Version, die ich ausprobiert hatte, gab es entlang des Äquators Unterbrechungen in der Verteilung der Verzerrungen.
Es war (für mich) eine einigermaßen zeitaufwendige Aufgabe, Konfigurationen für die beiden Hemisphären zu finden, die am Äquators nahtlos zusammenpassen.
Und am Ende stellte sich heraus, dass die asymmetrische Variante möglicherweise gar keinen Vorteil im Vergleich zu einer entsprechenden symmetrischen Variante zu bieten hatte.

Aber vor einiger Zeit fiel mir auf, dass es eine Familie von Kartennetzentwürfen gibt, die konfigurierbar ist und die es mir erlaubt, asymmetrische Projektionen zu erstellen, bei denen die beiden Hemisphären am Äquator immer perfekt zusammenpassen, ganz ohne Unterbrechungen und ohne den Aufwand, die richtigen Parameter zu finden.
Problem Nr. 1 und 2 waren also gelöst, und was die Nr. 3 angeht – wir werden sehen.

Ein Hinweis noch: Die Cupola-Projektion hat ein sehr spezifisches Ziel und wurde mathematisch entwickelt, um es zu erreichen. Die Projektionen, die ich heute zeige, sind weniger spezifisch: Wie der asymmetrische Wagner VII.b bemühen sie sich nur, eine Verteilung von Verzerrungen zu erreichen, die sich für die Kontinentalflächen beider Hemisphären (mit der Ausnahme von Antarktika) als vorteilhaft erweist.

Asymmetrische Varianten der Strebe-Projektionen von 1992

Vor etwa dreieinhalb Jahren habe ich einen Blogpost über die flächentreuen Strebe-Projektionen von 1992 verfasst – lies ihn, wenn du genaue Informationen über diese Projektionen haben möchtest. Ich fasse jetzt nur mal schnell zusammen: Bei diesen handelt sich um Transformationen von sechst existierenden Entwürfen (Sinusoidal, Mollweide, Hammer, Kavraiskiy V, Snyders Minimum-Error Pointed-Pole und Flat-Pole), die konfiguriert werden können durch einen Parameter, der die Krümmung der (Pseudo-) Pollinie festlegt. Dieser heißt in Geocart μ – der altgriechische Buchstabe My, sprich Mü –, oder Bonne φ₁ in Strebes Abhandlung von 2018.^[1]
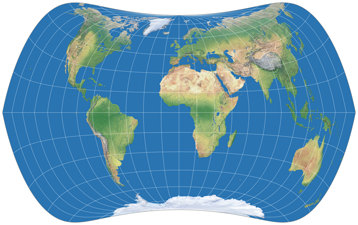
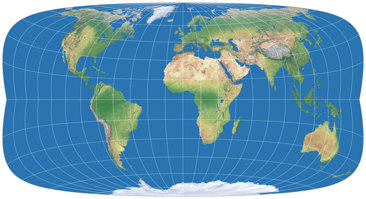
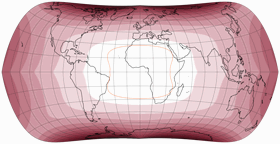
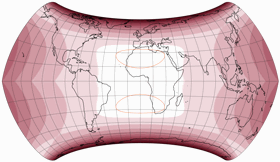
Bei μ handelt es sich um eine geografische Breite, der Umfang der erlaubten Werte unterscheidet sich bei den verschiedenen Projektionen, z.B. beim Strebe-Mollweide muss er zwischen 43°N and 29°S liegen; jeder Wert erzeugt ein anderes Ergebnis. Schauen wir uns mal die genannte Projektion an, zweimal mit einem μ von 24°, aber 24° Nord im ersten Bild und 24° Süd (wie im Titelbild meines 2022er Projektionskalenders) im zweiten:

Beide zeigen die für diese Projektionsreihe typischen »Knicke« in den Meridianen am Äquator. Ansonsten sind die Resultate höchst unterschiedlich – aber was für mich interessant war: Erzeugt man beide Variante mit dem gleichen nominellen Maßstab, passen sie am Äquator genau zusammen! Und das gilt für alle der 1992er Strebe-Projektionen. Die mühsame Suche nach den richtigen Werten, aus denen ich eine kontinuierliche Karte basteln kann, entfällt also völlig. Alles, was ich tun muss, ist:
– die nördliche Hemisphäre mit einem nördlichen Wert von μ rendern;
– die südliche Hemisphäre mit dem gleichen südlichen Wert rendern;
– die beiden Hemisphären zusammenfügen.

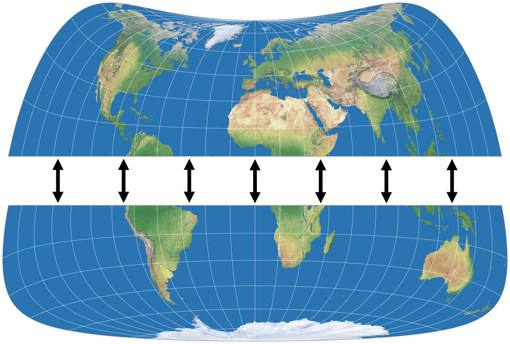
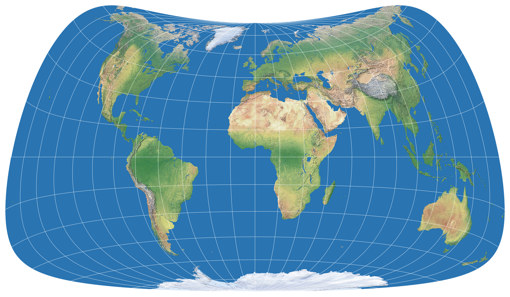
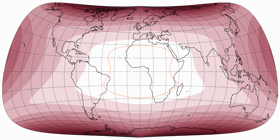
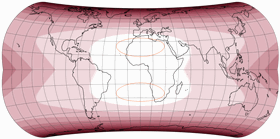
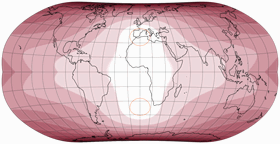
… und schon haben wir die erste Projektion dieser Reihe, den Strebe-Mollweide Asymmetrisch 24:

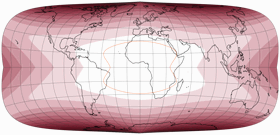
Der erste positive Effekt: Die Knicke am Äquator sind verschwunden, die Gradnetzlinien gehen nun kontinuierlich von der einen zur anderen Hemisphäre ineinander über. Was ist nun mit dem oben erwähnten Problem Nr. 3, das ich mit dem asymmetrischen Wagner VII.b hatte? Sieh selbst, hier ist die symmetrische Strebe-Mollweide mit μ = 24°N und noch einmal mit μ = 24°S … und dazwischen die asymmetrische Variante, die aus ihnen zusammengesetzt wurde. Zwar gibt es wieder einige Teile der nördlichen Hemisphären, die mit der »südlichen Variante« besser bedient sind, aber summa summarum kann man wohl sagen, dass dieses Mal beide Hemisphären gut bedient werden.

🌐

Nachdem ich das herausgefunden hatte, habe ich natürlich ausprobiert, ob sich auch für andere Projektionen der Serie eine vorteilhafte Nord-Süd-Kombination finden lässt. Bei Strebe-Hammer und Strebe-Sinusoidal habe keine solche gefunden (was nicht heißt, dass es sie nicht gibt, sondern nur, dass ich keine Konfiguration gefunden habe, die mir gefällt). Aber der Strebe-Kavraiskiy-V with μ = 20° N/S ist nicht übel:

Na gut, alles über ungefähr 75°N sieht ein bisschen so aus, als würde es in einen Staubsauger gesogen, welcher sich am Nordpol befindet… Nichtsdestoweniger, mit dem zurückhaltenden Ausmaß an Asymmetrie, der fast geraden Pseudo-Pollinie (»pseudo«, weil es hier keine echte Pollinie, sondern punktförmige Pole gibt) und einer äußeren Form, welche sich einem Rechteck annähert, mag es ein passendes Beispiel sein, wenn man sich nicht zu weit aus dem Fenster lehnen will.
Zu Vergleich der drei Varianten – ich denke, die Situation ist sehr ähnlich wie oben beim Strebe-Mollweide:

🌐

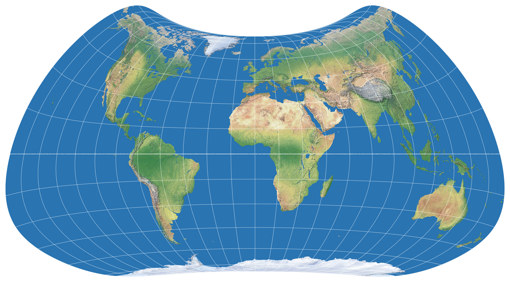
Das nächste Beispiel ist der einzige heute gezeigt Entwurf, der über eine echte Pollinie verfügt. Es handelt sich um den Strebe-Snyder Flat-Pole, abermals mit μ = 20° N/S. Da es in meinen Augen zu breit ausfiel, habe ich eine flächenerhaltende vertikale Streckung^[2] um 1,05 hinzugefügt:

Ehrlich gesagt, bin ich nicht sehr begeistert von dieser Variante – sie zeigt das typische Problem von äquivalenten Projektionen mit einer langen Pol-Linie: Die polarnahen Bereiche sehen ziemlich »gequetscht« aus. Ich habe schon drüber nachgedacht, sie zu verwerfen, aber ich wollte einen Entwurf mit linienförmigen Polen in der Sammlung beibehalten. Aber noch wichtiger: Die Position von Neuseeland in der »Ecke« der Karte (in der äquatorständigen Ansicht, zentriert auf den Nullmeridian) hat bei den anderen Projektionen dieser Serie zur Folge, dass das Ausmaß der Winkelverzerrungen über das Land hinweg stark variiert. Bei o.g. Varianten von Strebe-Mollweide und Strebe-Kavraiskiy zum Beispiel beträgt die Winkelverzerrung etwa 20° an der nördlichsten Spitze, aber etwa 45° an der südlichsten Spitze. Aber bei der hier gezeigten Konfiguration des Strebe-Snyder Flat-Pole liegt sie etwa zwischen 22° und 29° – was immer noch beachtlich ist für solche einer eher kleine Fläche, aber immerhin eine Verbesserung darstellt.

Bemerkenswert ist auch, dass dieser Entwurf von allen hier gezeigten die größte Landfläche aufweist, die unter einer Winkelverformung von 20° verbleibt. Was ein guter Grund ist, ihn trotz meiner ästhetischen Vorbehalte beizubehalten.

🌐

Den Abschluss bilden zwei Kompositionen des Strebe-Snyder Pointed-Pole.
Die erste wird aus den Hemisphären mit μ = 20° Nord/Süd zusammengesetzt. Obwohl sie punktförmige Pole hat, ist sie nicht so weit weg vom Wagner VII, dem vermutlich bekanntesten lentikulären flächentreuen Entwurf mit Pollinie (nur im Sinne des »allgemeinen Erscheinungsbildes«, natürlich gibt es deutliche Unterschiede): Strebe-Snyder Pointed-Pole Asymmetrisch 20 vs. Wagner VII

Der Längenverhältnis der Hauptachsen beträgt fast genau 2:1, was auch für den obigen Strebe-Kavraiskiy gilt. Der Letztgenannte hat eine bessere südliche Hemisphäre, und auch auf der nördlichen fallen große Teile der Kontinente besser aus. Nichtsdestoweniger muss ich sagen, dass ich den Strebe-Snyder PP 20 als etwas gefälliger empfinde.

🌐

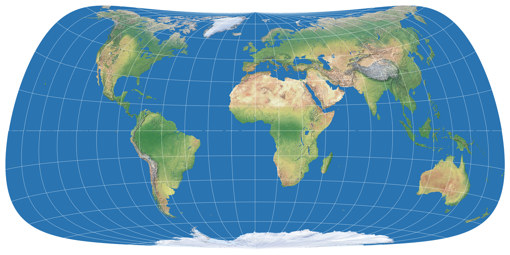
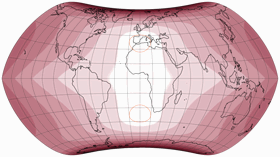
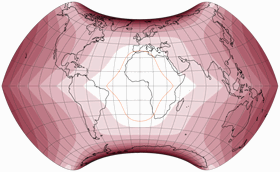
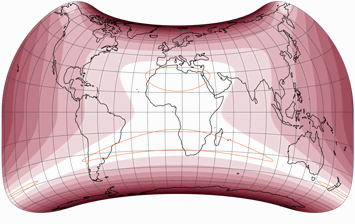
Und dann habe ich den Strebe-Snyder Pointed-Pole noch einmal mit einer ausgeprägteren Asymmetrie ausprobiert, nämlich mit μ = 26° N/S. Abermals habe ich das Seitenverhältnis leicht angepasst, aber diesmal habe ich eine horizontale Streckung von 1,05 verwendet (abermals flächenerhaltend).

Die ausgeprägte Krümmung der nördlichen Pollinie mag nicht jedermanns Sache sein, aber ich denke schon, dass dies die Verteilung der Verzerrungen für die (meisten) Landflächen auf beiden Hemisphären verbessert.
Dies ist mein persönlicher Favorit der hier vorgestellten Projektionen.

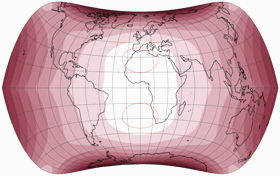
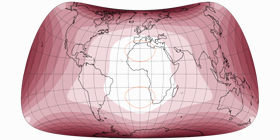
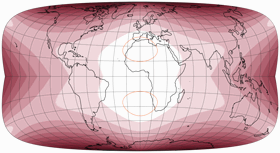
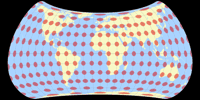
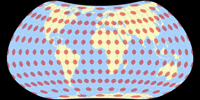
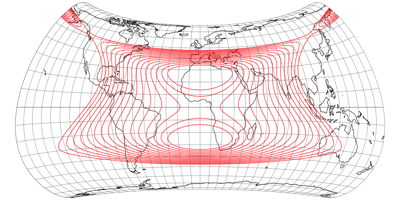
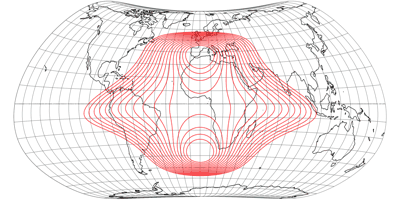
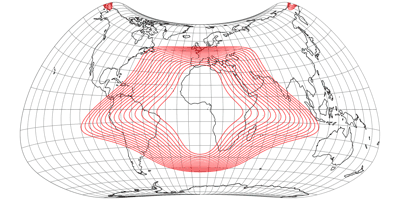
Keine Diskontinuitäten

Es wurde aus den oben gezeigten Verzerrungsgrafiken eigentlich schon deutlich, aber um zu zeigen, dass die Kompositionen am Äquator keine Unterbrechungen in der Verteilung der Verzerrungen aufweisen, zeige ich hier noch Darstellungen mit Isolinien der Winkelverformungen von 5 bis 20°:

Fazit

Strebes 1992er Serie von flächentreuen Projektionen bieten einen einfachen Weg, mit Asymmetrie zu experimentieren, ohne jegliche Probleme oder die Notwendigkeit, Berechnungen anzustellen. Die hier gezeigten Ergebnisse sind sicher nicht spektakulär, aber meiner Meinung nach durchaus gebrauchstauglich. Leider zeigt keine meiner Konfigurationen eine derart vorteilhafte Verteilung von Verzerrungen wie der Strebe Asymmetrisch 2011. Aber das war eigentlich zu erwarten…

Strebe Asymmetrisch 2011

Quellenangaben

↑ Strebe, Daniel (2018): A bevy of area-preserving transforms for map projection designers.
verfügbar auf researchgate.net
↑ Eine flächenerhaltende Streckung bedeutet, dass man die Höhe mit einem bestimmten Wert multipliziert und die Breite mit dem Kehrwert davon; z.B. wenn die Höhe mit 1,05 malgenommen wird, multipliziert man die Breite mit 1/1,05 = 0,95238095.

Permalink