Mo, 18.9.2017 Neues auf kartenprojektionen.de
Ein vergleichsweise großes Update mit mehreren Änderungen, die teilweise (zumindest »hinter den Kulissen«) miteinander zusammenhängen.
Der Blog geht online
… naja, das ist offensichtlich.
Schließlich liest Du ihn ja gerade. ;-)
Falls Dich die Beweggründe interessieren: Über die lasse ich mich
im allersten Blogpost aus.
Neue Version der Projektionsgrafiken
Die physischen Karten mit Relief-Darstellung des Ozeanbodens wurden für
(fast) alle Projektionen durch eine neue Version ersetzt. Der Unterschied
ist zugegebenermaßen eher geringfügig, war mir aber dennoch wichtig.
Die Karten mit flachen, einfarbigen Ozeanen werden in Kürze auch ersetzt.
Das Thema behandele ich ausführlich in einem eigenen Blog-Eintrag.
Neue Projektionen
Es ist eine Handvoll neuer Projektionen hinzugekommen:
Bottomley (in zwei Konfigurationen), Breusing Geometric, Cabot (in zwei Konfigurationen).
Darüber hinaus gibt es auch zusätzliche Konfigurationen von Projektionen, die bereits
im Vergleich enthalten waren: Der unterbrochene McBryde S2, die flächen- und die längentreue Kegelprojektion,
die Sinusoidal-Projektion im sinoidalen Unterbrechungsschema, sowie eine ungewöhnliche
(und meines Wissens in dieser Art noch nie irgendwo vorgestellte) unterbrochene Variante
des Wagner VII.
Mehr über die Cabot-Projektion im eigenen Blogpost. Über die neuen Kegelprojektion, siehe unten.
Änderung bei den unterbrochenen Projektionen
Bisher wurden alle unterbrochenen Projektionen im Goodeschen Unterbrechungsschema gezeigt. Die Idee dahinter war, auf diese Weise eine bessere Vergleichbarkeit zu schaffen. Rückblickend muss ich sagen, dass diese Idee von vornherein nicht die beste war: Wenn ein Kartograph ein eigenes Unterbrechungsschema vorgelegt hat, sollte ich dieses Schema bei einen eigenen Entwürfen auch nutzen! Daher werden die Projektionen von Boggs und McBryde nun im jeweiligen Unterbrechungsschema ihrer Urheber gezeigt.
Kleinere Änderungen bei den Projektionsgrafiken
Bei zwei Projektionen wurden die Grafiken geringfügig überarbeitet.
Die Albers-Projektion war zuvor unten und oben ein wenig beschnitten, jetzt wird eine komplette Darstellung gezeigt.
Laskowskis Tri-Optimal-Projektion eine besondere Eigenheit: Die Pol-Linie beschreibt eine Schleife. Dies wird sehr deutlich in einer Darstellung wie folgt – und es handelt sich tatsächlich um eine Schleife, nicht etwa zwei »Hörner«, deren Spitzen sich berühren.
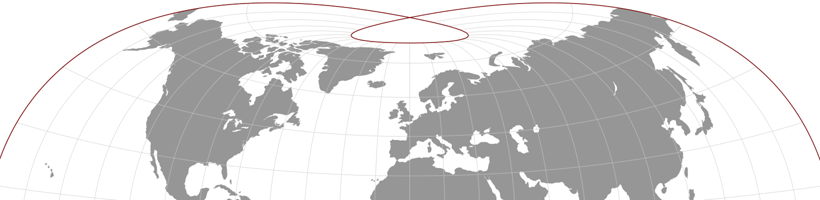
Nichtsdestoweniger wirkte die bisherige Grafik eher so, als handele sich um »Hörner«. In der neuen Grafik ist die Schleife (hoffentlich!) besser zu erkennen.
Änderungen bei den konischen Projektionen
Das ist jetzt ein bisschen verwirrend. Ich versuche mal, es einigermaßen verständlich zu erklären.
Die Projektion, die vorher Lamberts flächentreue Kegelprojektion hieß,
wird jetzt unter dem Namen CM Lamberts flächentreue Kegelprojektion geführt.
Das CM steht dabei für »compare maps« (vergleiche Karten) und soll andeuten, dass es sich um
eine eher ungewöhnliche Konfiguration handelt, die nur zu Vergleichszwecken dient.
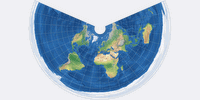
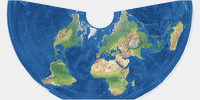
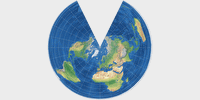Den dadurch freigewordenen Namen Lamberts flächentreue Kegelprojektion
trägt jetzt eine andere Konfiguration. Diese dürfte öfter zu sehen sein – und ist
meiner Meinung nach auch besser geeignet, die gesamte Erde darzustellen.
Die Projektion CM Längentreue Kegelprojektion –
nun, die heißt noch genauso wie vorher, und hat sich auch optisch nicht verändert.
;-)
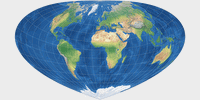
Eine neue (ebenfalls üblichere) Varianten des vorgenannten Entwurfs wurde neu
aufgenommen und heißt 20/60N Längentreue Kegelprojektion
(da hier die Schnittparallelen auf 20 und 60° Nord gelegt wurden).
Soweit die Neuheiten.
Wie geht’s weiter? Ganz oben auf meiner ToDo-Liste sind natürlich die neuen Grafiken für die Projektionen
mit flacher Ozean-Darstellung. Damit habe ich auch schon angefangen, aber das dauert halt…
Ansonsten habe ich auch schon ein paar Artikel im Kopf, welche ich im Blog veröffentlichen werde.
Wartet’s einfach ab!
Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Kommentare
Sei der erste, der einen Kommentar hinterlässt!