13 Projektionen für 2022 (Teil 3)

Do, 3.3.2022 13 Projektionen für 2022 (Teil 3)

Eine Kollektion meiner eigenen Experimente
(siehe Intro für weitere Erklärungen)

März: Canters-Frančula

Canters-Frančula
Original-Urheber	Nedjeljko Frančula / Frank Canters (1971 / 2002)
Gruppe	Lentikulär
Eigenschaft	Vermittelnd
Anmerkungen	Eine Fusion von Canters W09 (nördliche Hemisphäre) und Frančula XIII (südliche Hemisphäre).
Meine Variante	2021 entwickelt, hier erstmals vorgestellt

Der Kalender dieses Jahres handelt von meinen Experimenten, und Experimente gehen manchmal schief.
Die heute gezeigte Projektion mag vielleicht kein echter Fehlschlag sein, aber sie hat eine gewisse Unzulänglichkeit.

Es handelt sich um eine Fusion von zwei existierenden Projektionen; beides sind optimierte Varianten des Wagner IX.i: Frančula XIII^[1] und Canters W09^[2] (siehe auch meine Blogposts über die Frančula- und Canters-Projektionen). Ich mag sie beide; aber es fiel mir auf, dass die Verteilung der Winkelverformungen auf den Landmassen der südlichen Hemisphäre beim Frančula XIII etwas vorteilhafter ausfällt – und umgekehrt der Canters W09 auf der nördlichen Hemisphäre gewisse Vorteile hat.

Bei der Verteilung der Flächenvergrößerungen auf den Kontinente nehmen sich die beiden Entwürfe nicht viel, obgleich ich unterm Strich leichte Vorteile beim Frančula sehe.

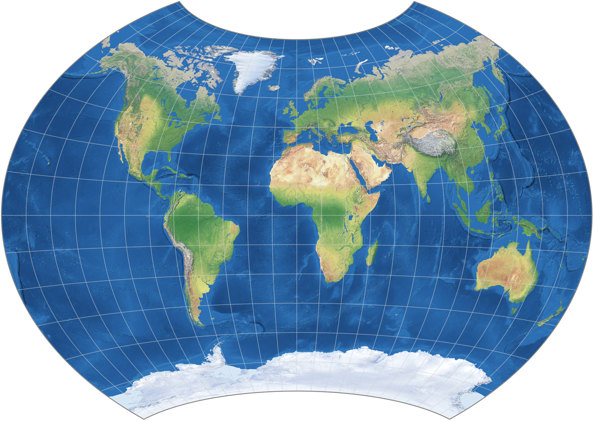
Also dachte ich: Nimm das beste aus beiden Welten (Wortspiel beabsichtigt), kleb die nördliche Hemisphäre des Canters W09 und die südliche Hemisphäre des Frančula XIII zusammen! Bei beiden war eine kleine Anpassung des Seitenverhältnisses vonnöten, damit sie am Äquator zusammenpassen: Der Frančula wurde in Ost-West-Richtung ein wenig zusammengedrückt, der Canters gestreckt. Das Resultat ist oben zu sehen.

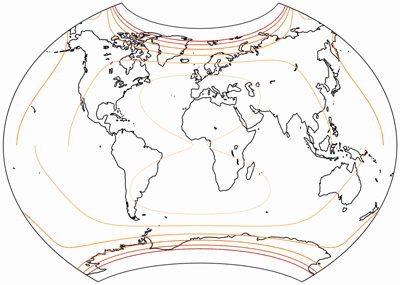
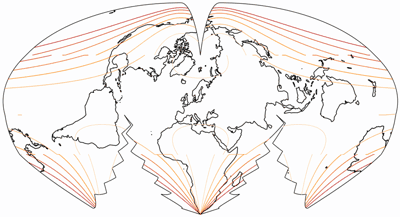
Aber obwohl mir diese Komposition optisch gut gefällt, muss ich zugeben, dass sie nicht ohne Mangel ist. Betrachte die Isolinien der Winkelverformungen und Flächenvergrößerungen:

Die Isolinien werden gezeigt für eine maximale Winkelverzerrung von:
10°, 20°, 30°, 40°, 50°, und 60°.
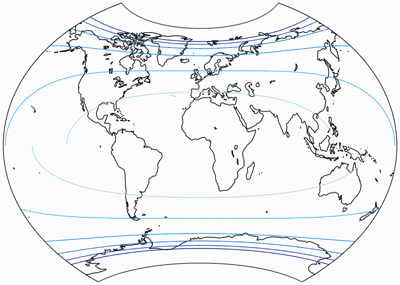
Bei der Flächenvergrößerung, gezeigt im Verhältnis zum Wert in der Mitte der Karte, repräsentieren die Linien Werte von:
1,2; 1,5; 2,0; 2,5; 3,0; und 3,5.

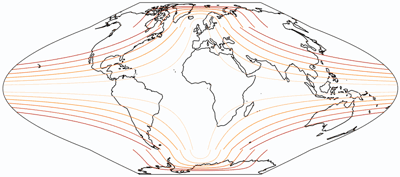
Wie du sehen kannst, sind die Linien unterbrochen – am Äquator treten Diskontinuitäten in der Verteilung der Verzerrungen auf. So etwas ist nicht ohne Beispiel, tatsächlich treten gleichartige Unterbrechungen in verschiedenen zusammengesetzten Projektionen auf: Um nur ein paar zu nennen, McBryde S3, Goodes berühmter Homolosine und der wunderschönen Philbrick Sinu-Mollweide … all dies sind zusammengesetzte Projektionen^[3], und sie alle zeigen Diskontinuitäten in den Verzerrungen.

Zunächst war ich der Ansicht, dass der Canters-Frančula vielleicht für einen netten Eintrag im Kalender ausreichend sei, aber wegen dieser Diskontinuitäten nicht gut genug, um in der Liste auf meiner Website zu erscheinen … aber dann dachte ich: Wenn solche bekannten, schönen Projektionen sie haben dürfen, dann kann ich sie auch bei einem eigenen Experiment erlauben.
Und daher wird die Canters-Frančula-Projektion in Kürze hinzugefügt.

Wir sind durch.
Nächsten Monat haben wir… ääähmmm… April.

Quellenangaben / Fußnoten

↑ Nedjeljko Frančula, 1971: Die vorteilhaftesten Abbildungen in der Atlaskartographie
↑ Frank Canters:
Small-scale Map Projection Design.
London & New York 2002.
↑ McBryde S3 ist eine Fusion aus der sinusoidalen Projektion und McBryde-Thomas Flat-Polar Sinusoidal, zusammengefügt bei 55°51′N/S; Goodes Homolosine aus Sinusoidal und Mollweide bei 40°44′N/S; Sinu-Mollweide ebenfalls aus den beiden letztgenannten, allerdings bei 40°44′S (vor der Rotation des Kartenzentrums).