So, 2.10.2022 13 Projektionen für 2022 (Teil 10)
Eine Kollektion meiner eigenen Experimente
(siehe Intro für weitere Erklärungen)
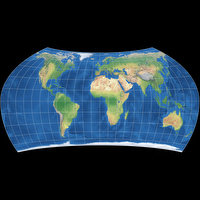
Oktober: Canters W30/UA (nicht optimiert)
| Canters W30/UA (nicht optimiert) | |
|---|---|
| Original-Urheber | Frank Canters (2002) |
| Gruppe | Lentikulär |
| Eigenschaft | Vermittelnd |
| Anmerkungen | Eine umbezifferte, aphylaktische (= vermittelnde) Variante des Canters W30. Nicht für niedrige Verzerrungswerte optimiert. |
| Meine Variante | 2021 entwickelt, hier erstmals vorgestellt. |
Seit dem Start meiner Website im Jahr 2015 habe ich einige der Projektionen von Frank Canters aufgelistet. Nach und nach habe ich weitere hinzugefügt. 2021 habe ich dann die komplette Reihe von Weltkarten-Projektionen, die Canters in seinem Fachbuch von 2002[1] vorgestellt hat, vervollständigt und sie in einem zweiteiligen Artikel besprochen.[2]
Zu ihnen gehört die Projektion Canters W30[3] (eine flächentreue Post-Transformation des Wagner VII), welche sich durch vergleichsweise gute Verzerrungswerte auszeichnet (gemäß Canters’ eigener Metrik):
Mir gefällt dieser Entwurf, aber er sieht sicherlich recht ungewöhnlich aus. Vielleicht würde ein bisschen Umbeziffern[4] helfen, die seltsame Form etwas zu beruhigen? Einen Versuch ist es wert! Die Länge der Pol-Linie habe ich nicht verändert, aber den begrenzenden Meridian auf 150°O/W gesetzt. Das Resultat war eine flächentreue Karte, die vielversprechend aussah (auf diese komme ich gleich noch einmal zurück). Dann habe ich noch eine gewisse Menge Flächenvergrößerung (1,35-fache Vergrößerung bei 60°N/S) und eine horizontale Kompression hinzugefügt (indem ich das Längenverhältnis der Hauptsachen auf 1:1,8 anstelle von 1:2 gesetzt habe) – Voilà, dies ist die Konfiguration, die du am Anfang dieses Blogposts sehen kannst!
Wenn ich die Möglichkeit hätte, die Gesamtverzerrungswerte zu messen oder wenigstens die Isolinien der Winkelverformungen und Flächenvergrößerungen darzustellen, hätte ich vermutlich noch weiter experimentiert. Aber das habe ich nicht, also bin ich dabei belassen. Meiner Meinung nach war diese Variante gut genug, um in den Kalender aufgenommen zu werden – und auch in meine Projektions-Kollektion. Daher habe ich sie heute hinzugefügt, zusammen mit dem o.g. flächentreuen Zwischenergebnis. In Bezug auf die Gesamtverzerrungen nehme ich an, dass beide nichts Besonderes sind, aber auch nicht wirklich schlecht abschneiden würden.

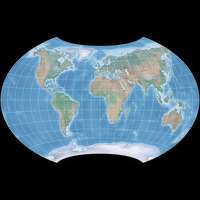
Die flächentreue Variante:
Canters W30/UE (nicht optimiert)
Was die Benennung der zwei Entwürfe angeht:
Im gedruckten Kalender habe ich die Projektion
Canters W30/UA genannt (U für Umbeziffern, A für aphylaktisch).
Folglich wäre die flächentreue Variante dann Canters W30/UE
(engl. equal-area = flächentreu)…
Aber dann hatte ich Zweifel. Frank Canters hat die eigentliche Arbeit erledigt, also
ist es angemessen, die Projektion nach ihm zu benennen.
Andererseits: Alle Canters-Projektionen wurden mathematisch für niedrige Verzerrungswerte
optimiert. Die Verwendung seines Namens könnte also zu der Annahme führen, dass meine
Varianten auf die gleiche Weise optimiert wurden, was definitiv nicht der Fall ist.
Wie konnte ich diesen Konflikt auflösen?
Nachdem ich eine Weile darüber nachgedacht hatte, stellte ich fest, dass es unmöglich ist,
Canters’ Namen zu verwenden und gleichzeitig nicht zu verwenden 😉,
also befolgte ich dem Vorschlag von Peter Denner, den Zusatz »(nicht optimiert)« anzuhängen.
Die verbleibenden zwei Projektionen des diesjährigen Kalenders sind nicht
neu, ich habe sie Euch schon präsentiert.
Nebenbei bemerkt, ich bin im Moment noch nicht sicher, ob es auch einen
2023er Kalender geben wird. Hauptsächlich, weil ich noch keine Idee
für ein Leitmotiv habe. Falls dir da etwas einfällt, poste es doch
bitte in den Kommentaren unten.
Quellenangaben / Fußnoten
-
↑
Frank Canters:
Small-scale Map Projection Design.
London & New York 2002. - ↑ Siehe Die Canters-Projektionen, Teil 1 and Teil 2.
- ↑ Canters selbst hat diese Projektion Low-error equal-area transformation of Hammer-Wagner with twofold symmetry and correct ratio of the axes (Flächentreue Low-Error Post-Transformation des Hammer-Wagner, doppeltsymmetrisch, achsverhältniswahrend) genannt, aber ich habe das von Dr. Rolf Böhm vorgestellte Bezeichnungsschema übernommen. Mehr zu diesem Thema gibt es im Artikel Benennung der Canters-Entwürfe.
- ↑ Mehr Informationen über Wagners Transformationsmethode, »das Umbeziffern«, gibt es im Artikel Das Umbeziffern oder kürzer in diesem Blogpost oder in den Hinweisen beim Wagner-Variationen-Generator (WVG-7).
Mein Kartenprojektions-Kalender 2022
Um einen anderen Teil der Serie meines 2022er Kartenprojektions-Kalenders zu lesen, wähle den gewünschten Monat aus.














 Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Sofern nicht anders angegeben, sind Grafiken lizenziert unter
Kommentare
Sei der erste, der einen Kommentar hinterlässt!