13 Projektionen für 2023 (Teil 4)

Di, 18.4.2023 13 Projektionen für 2023 (Teil 4)

Eine Kollektion von Projektionen für politische Weltkarten
(siehe Intro für weitere Erklärungen)

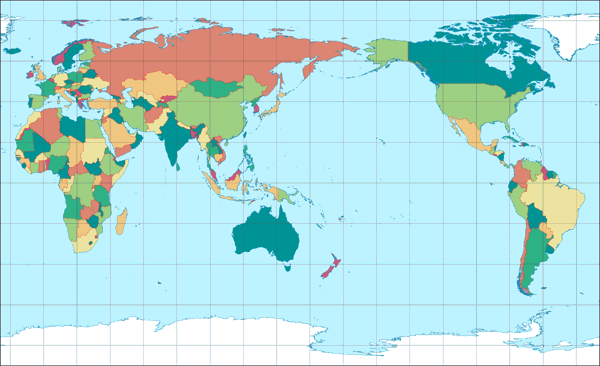
April: Rektangularprojektion

Rektangularprojektion
Urheber	Marinos von Tyros (ca. 100 n.Chr.)
Gruppe	Zylinder
Eigenschaft	Längentreu
Andere Namen	Rechteckige Plattkarte
Anmerkungen	Hier: 35° Nord/Süd als Schnittparallelen.

Normalerweise bin ich nicht gerade begeistert von zylindrischen Projektionen. Aber angesichts der Tatsache, dass ich vor einigen Jahren eine beschriftete politische Karte selbst angefertigt und mich aus guten Gründen für eine zylindrische Projektion habe – und es ist eine Karte, auf die ich regelmäßig zurückgreife –, kann ich wohl kaum von dieser Gruppe der Projektion abraten, was?

Außerdem, wie ich schon wiederholt gesagt habe, scheinen die Leute rechteckige Karten in Allgemeinen und im Besonderen jene mit geraden Meridianen und Breitenkreisen (also die zylindrische Projektionen) zu lieben. Der mathematisch einfachste (und sogar einfachst mögliche) Entwurf dieser Art ist die Rektangularprojektion (auch rechteckige Plattkarte genannt), und meiner Meinung nach ist er nichtsdestoweniger für viele Zwecke besser geeignet als andere Zylinderprojektionen. Wenn du dir nämlich andere nicht-flächentreue zylindrische Projektionen ansiehst, wirst du feststellen, dass die meisten von ihnen^[1] zu den Polen hin eine signifikant höhere Flächenvergrößerung aufweisen.

Durch die Verwendung von Schnittparallelen^[2] kann die Projektion horizontal gestaucht werden. Im oben gezeigten Bild habe ich mich für 35° Nord/Süd entschieden, weil die Karte so perfekt in den zu Verfügung stehenden Platz auf dem Kalenderblatt gepasst hat. Und darüber war ich sehr froh, denn ich bin der Meinung, dass die besten Ergebnisse mit Schnittparallelen zwischen 30° und 40° erzielt werden.

Nur so zum Spaß schauen wir uns mal diese kleine Sequenz an, welche die Rektangularprojektion mit Schnittparallelen auf 0, 10, 20, 30, 35, 40, 45, 50 und 60 Grad zeigt:

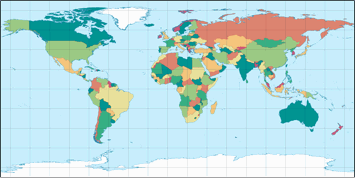
Die erste Variante mit dem Äquator als Schnittparallele (dieser Fall wird auch quadratische Plattkarte oder Plate-Carrée-Projektion genannt) ist in meinen Augen … nun, ganz okay, aber die Ost-West-Streckung der polnahen Gebiete ist fast schmerzhaft. Immerhin verfügt sie über das korrekte Längenverhältnis der Hauptachsen. Letzteres fällt bei den Varianten mit 10° und 20° weg, aber ohne eine echte Verbesserung bzgl. der Verteilung der Verzerrungen bieten zu können.

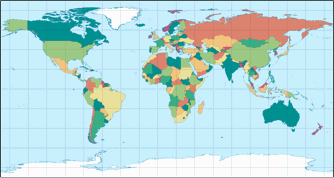
Schnittparallelen auf 30, 35, 40 Grad: Das sind die Konfigurationen, die ich für die Anwendung als politische Karte empfehlen würde. Schon 45° (diese Variante ist auch bekannt als Gall Isographisch) führen in meinen Augen zu einer unangenehmen Nord-Süd-Streckung; obgleich ich weiß, dass gewisse Verzerrungsmetriken Schnittparallelen in diesem Bereich als optimal ausweisen.^[3]

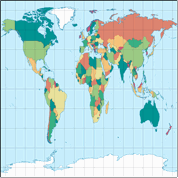
Die Verwendung von 50° N/S resultiert in einer Karte, die ziemlich häßlich ist. Sie ist in dieser Sequenz nur enthalten, damit ich noch bei der 60°-Variante ankomme, welche eine exakt quadratische Karte erzeugt. Ich weiß nicht, warum man so etwas haben wollen würde, aber ich bin sicher, so etwas kommt vor, also – hier hast du eine quadratische Karte.

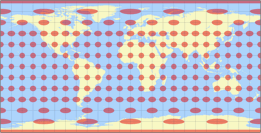
Da ich die Verteilung der Verzerrungen erwähnt habe, zeige ich hier noch einmal die gleichen Varianten wie oben, aber hier mit der tissotschen Indikatrix:

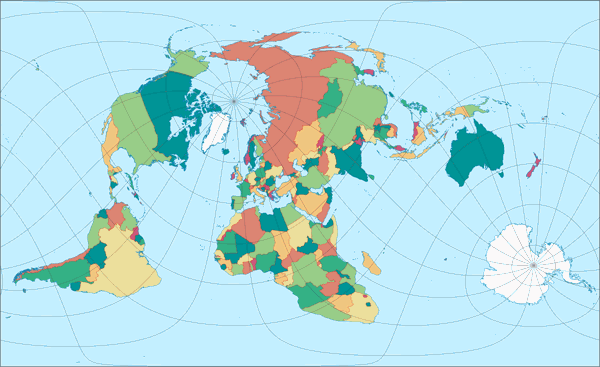
Und da dieser Blogpost immer noch nicht genug bunte Bilder hat, folgen jetzt noch die OGABO-Version sowie Karten mit den in Das Durchtrennen von Land minimieren erwähnten Projektionszentren, nämlich der plagale Aspekt und die Zentrierung auf 154° Ost:

Die OGABO-Version funktioniert bei Zylinderprojektionen natürlich sehr gut. Die plagale Lage fällt für einen Großteil der Landflächen recht ordentlich aus. Und die 154°O-Version – nun im o.g. Blogpost »Durchtrennen von Land minimieren«-Blogpost erwähnte ich einen »Haken bei den pazifikzentrierten Karten«. Der Haken ist, dass dieses Kartenzentrum nur bei zylindrischen Projektionen gut funktioniert. Andere Projektionsarten schieben die Verzerrungen an den Kartenrand, d.h. in den Pazifik, wenn das Zentrum auf dem oder nahe des Nullmeridians liegt. Unglücklicherweise befinden sich am Rand der Karte Kontinente, wenn sie auf den Pazifik zentriert ist.

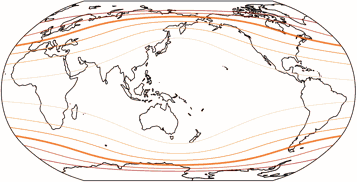
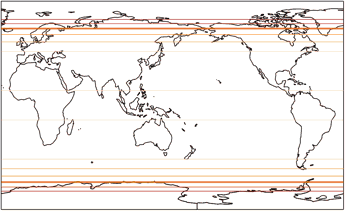
Vergleiche die Verteilung von Winkelverformungen beim Robinson (unserer Februar-Projektion), dem Wagner VII (März) und der Rektangularprojektion – und du siehst, warum es höchst empfehlenswert ist, für eine pazifikzentrierte Karte eine zylindrische Projektion zu wählen.

Die Isolinien werden gezeigt für eine maximale Winkelverzerrung von:
10°, 20°, 30°, 40°, 50°, und 60°.

Im Mai werden wir eine Projektion haben, die m.W. noch nie irgendwo benutzt worden ist, obgleich sie ganz und gar nicht »ungewöhnlich« ist.

Quellenangaben / Fußnoten

↑ »Die meisten«? Nö, eigentlich alle außer der Patterson-Projektion.
↑ Die Schnittparallele ist der Breitenkreis, der im richtigen Maßstand abgebildet ist, oder – so kann man es hier auch ausdrücken – der im korrekten Längenverhältnis zu den Meridianen gezeigt wird.
↑ Siehe das Posting von Peter Denner im Mapthematics-Forum, und die Antwort von »Atarimaster« (das bin ich).